Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Удивительный мир земных звезд
Содержание
- 1. Удивительный мир земных звезд
- 2. Математика владеет не только
- 3. Мир наш исполнен симметрии. С
- 4. Виды правильных многогранников
- 5. Теорема Эйлера Вершины + Грани - Рёбра
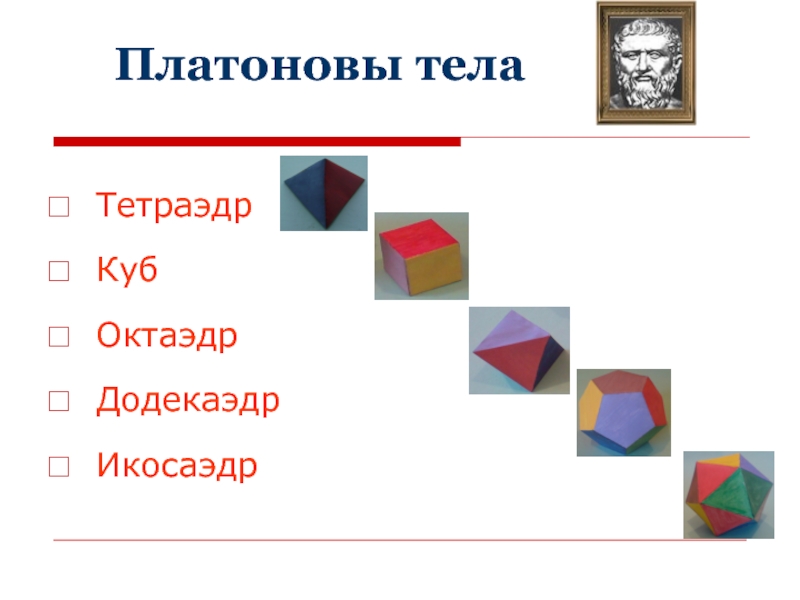
- 6. Платоновы телаТетраэдрКубОктаэдрДодекаэдрИкосаэдр
- 7. Архимедовы тела
- 8. Кубок Кеплера Вокруг
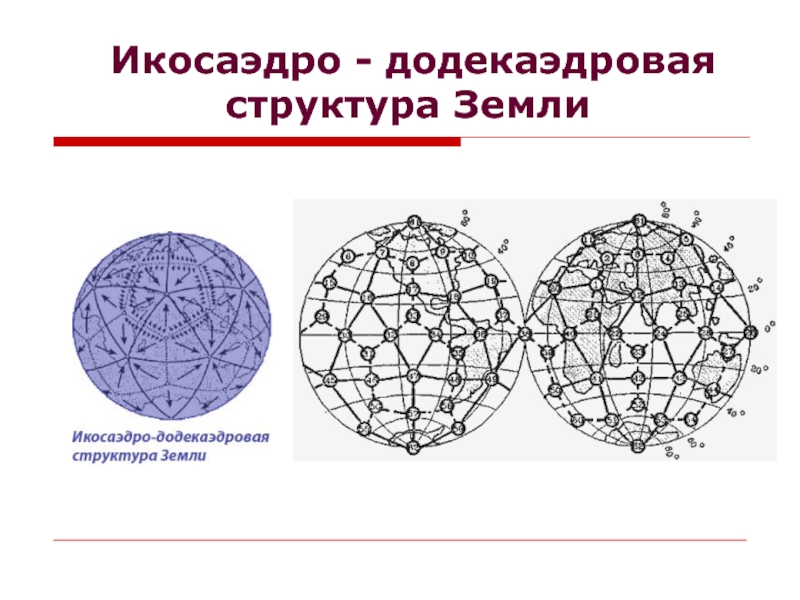
- 9. Икосаэдро - додекаэдровая
- 10. Слайд 10
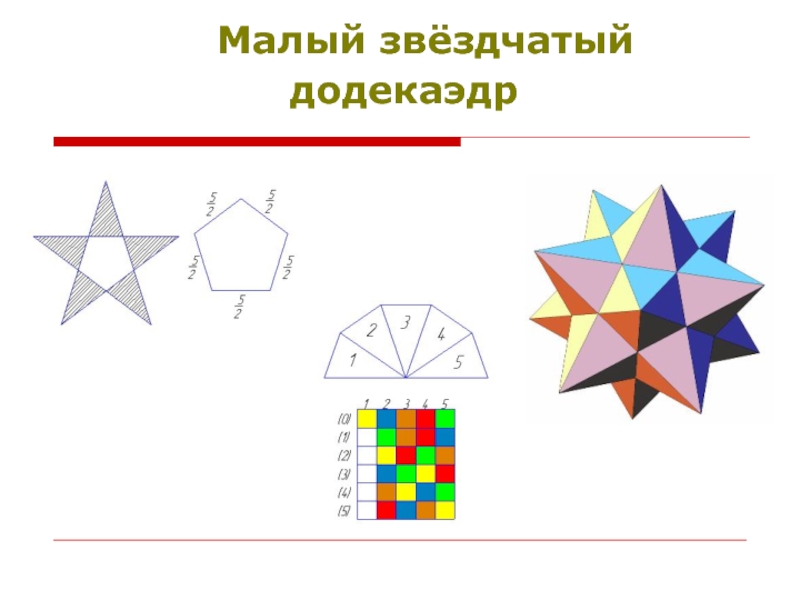
- 11. Тела Кеплера – ПуансонаЗвёздчатый октаэдр
- 12. Слайд 12
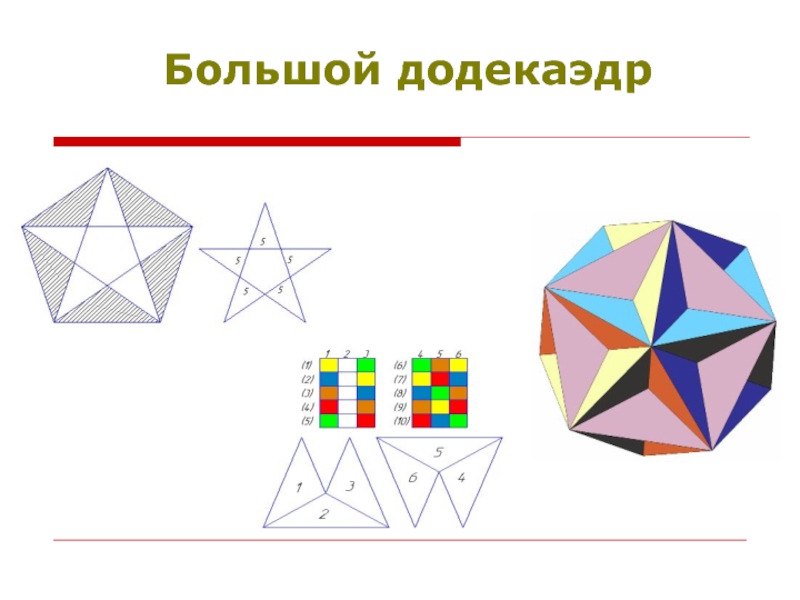
- 13. Большой додекаэдр
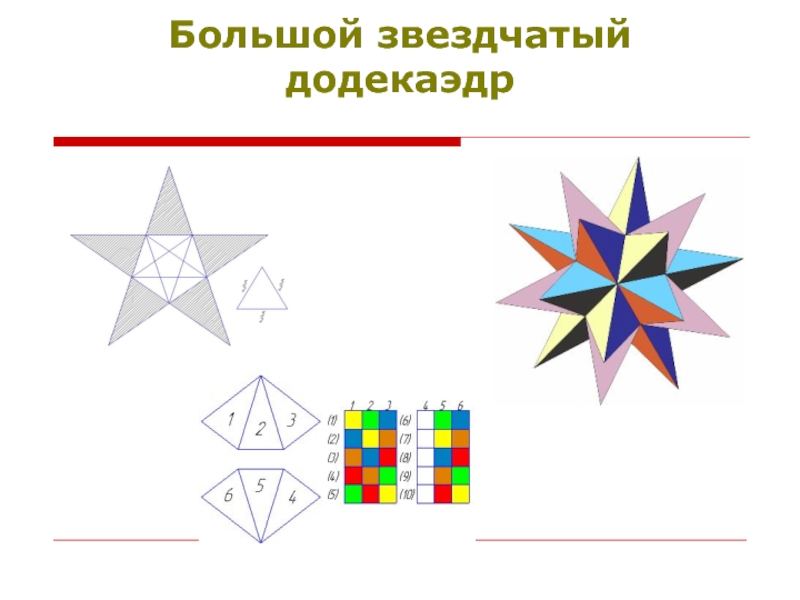
- 14. Большой звездчатый додекаэдр
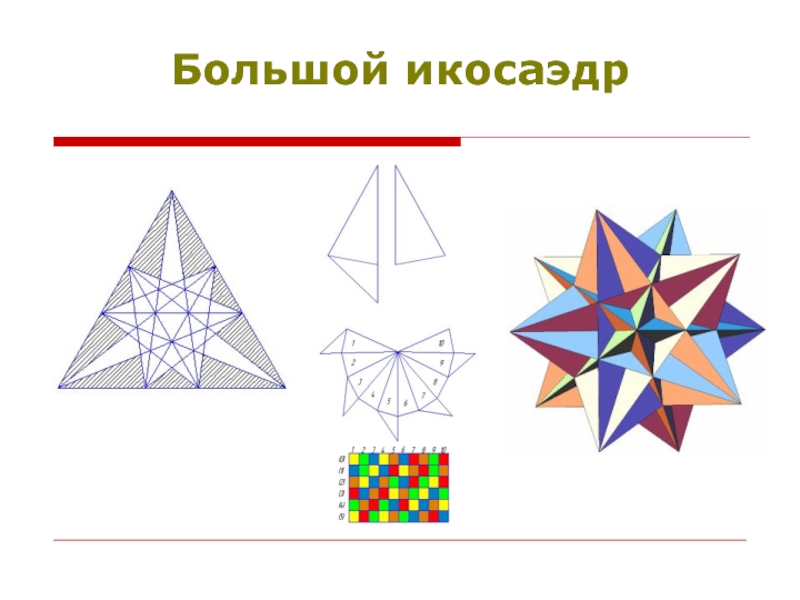
- 15. Большой икосаэдр
- 16. Слайд 16
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Автор: учитель математики 1 квалификационной категории Зайцева Галина Геннадиевна
Удивительный мир
земных звезд
Слайд 2 Математика владеет не только истиной, но и
высшей красотой – красотой отточенной и строгой, возвышенно чистой и
стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.Бертран Рассел
Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Слайд 3 Мир наш исполнен симметрии. С древнейших времен с
ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий
интерес человека к удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.Симметрия
Слайд 4 Виды правильных многогранников
Многогранник - геометрическое
тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны
граней называются ребрами многогранника, а концы ребер — вершинами многогранника.Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.
Выпуклый многогранник называется правильным, если все его грани — правильные одинаковые многоугольники и все многогранные углы при вершинах равны.
Слайд 5Теорема Эйлера
Вершины + Грани - Рёбра = 2.
Многогранник Вершины Грани Рёбра Оси симметрии Плоскости
симметрии
Тетраэдр 4 4 6 3 6
Куб 8 6 12 9 9
Октаэдр 6 8 12 9 7
Додекаэдр 20 12 30 15 15
Икосаэдр 12 20 30 15 15
Слайд 8 Кубок Кеплера
Вокруг сферы Меркурия описан
октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан
икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.Слайд 10 Теория многогранников, в частности
выпуклых многогранников, одна из самых увлекательных глав геометрии.
Л. А. ЛюстерникПирит (сернистый колчедан)