Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Универсальная формула 8 класс
Содержание
- 1. Универсальная формула 8 класс
- 2. Слайд 2
- 3. Замечательная формула, пригодная для вычисления объема цилиндра,
- 4. Слайд 4
- 5. Убедиться в правильности этой формулы очень легко
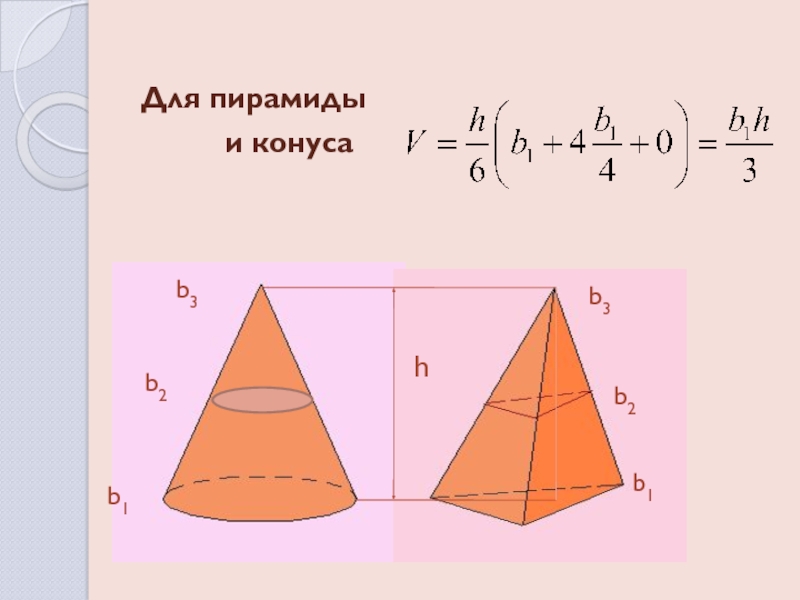
- 6. Для пирамиды и конуса
- 7. Для усеченного конусаДля усеченной пирамиды доказательство ведется сходным образом;
- 8. Для шара:
- 9. Можно отметить еще одну любопытную особенность универсальной
- 10. Чтобы в этом убедиться, применим формулу и получим: Для параллелограмма (квадрата, прямоугольника)
- 11. Для трапеции
- 12. Для треугольникаb2
- 13. Вы видите, что формула имеет достаточно прав называться универсальной.
- 14. Спасибо за внимание!
- 15. Материалы, использованные при подготовке презентации:1.Перельман Я.И. Занимательная геометрия. ГИТТЛ, М. 1957г.2. http://ru.wikipedia.org3. http://matematiku.ru
- 16. Скачать презентанцию
АннотацияЦель данного проекта – рассказать, как вычислить объемы простых тел и площади плоских фигур с помощью одной формулы, которая не встречается в школьных учебниках.
Слайды и текст этой презентации
Слайд 1Автор проектной работы- Пушкаш Максим Владимирович, 8 класс Руководитель-Сахно Людмила Николаевна МКОУ «Ступинская
СОШ№14»
«Геометрические миниатюры»
Слайд 2 Аннотация
Цель данного проекта
– рассказать, как вычислить объемы простых тел и площади плоских
фигур с помощью одной формулы, которая не встречается в школьных учебниках.Эта формула может пригодиться в практике, например, для измерения «объема ствола дерева, не интересуясь тем, на что он больше похож – на цилиндр или на конус, полный или усеченный»[1].
В работе показано применение формулы для различных тел и фигур.
Слайд 3Замечательная формула, пригодная для вычисления объема цилиндра, полного конуса, усеченного
конуса, всякого рода призм и пирамид и даже шара, известна
в математике под названием формулы Симпсона.То́мас Си́мпсон (1710-1761) — английский математик. С 1746 года Симпсон - член Лондонского королевского общества, с 1758 года - иностранный член Шведской королевской академии наук. Симпсон составил учебники по элементарной математике. В особых отделах геометрии рассматриваются задачи о наибольших и наименьших величинах, решаемые с помощью элементарной геометрии, правильные многогранники, измерение поверхностей, объёмы тел и, наконец, смешанные задачи [2].
Слайд 4 V
=
где
h – высота тела,
b1 – площадь нижнего основания,
b2 – площадь среднего сечения,
b3 - площадь верхнего основания
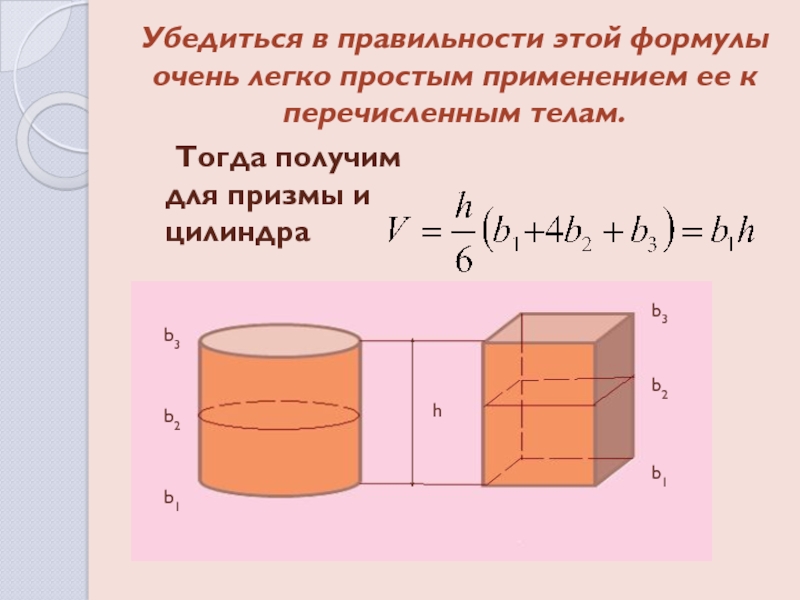
Слайд 5Убедиться в правильности этой формулы очень легко простым применением ее
к перечисленным телам.
Тогда получим для призмы и цилиндра
Слайд 9
Можно отметить еще одну любопытную особенность универсальной формулы: она годится
также для вычисления площадей плоских фигур – параллелограмма, трапеции и
треугольника,если h - это высота фигуры,
b1 - длина нижнего основания,
b2 - длина средней линии,
b3 - длина верхнего основания.
Слайд 10Чтобы в этом убедиться, применим формулу и получим:
Для параллелограмма (квадрата,
прямоугольника)
Слайд 15Материалы, использованные при подготовке презентации:
1.Перельман Я.И. Занимательная геометрия. ГИТТЛ, М.
1957г.
2. http://ru.wikipedia.org
3. http://matematiku.ru
