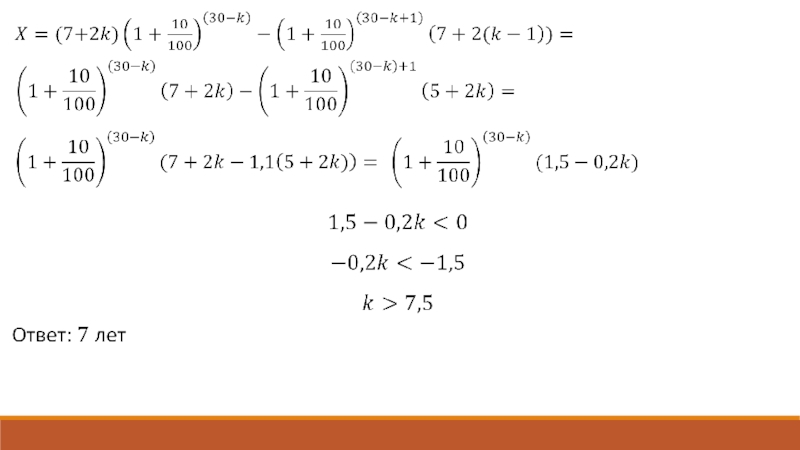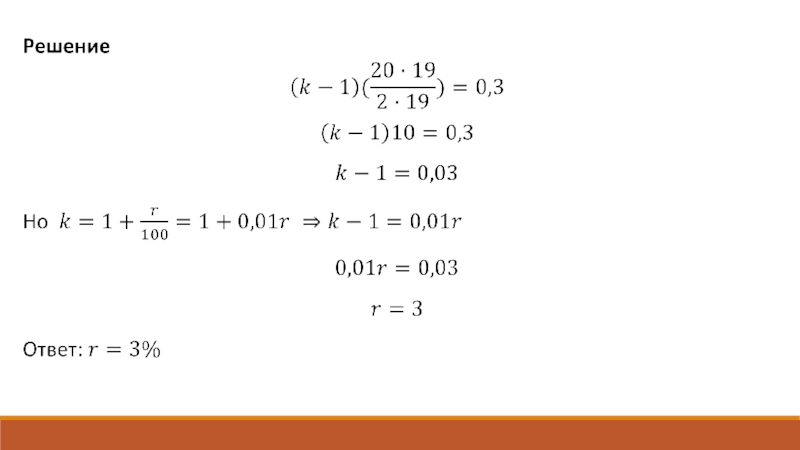Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи c экономическим содержанием в ЕГЭ
Содержание
- 1. Задачи c экономическим содержанием в ЕГЭ
- 2. Простые проценты. Налоги.
- 3. Сложные проценты. Вклады.или1) Величина S0 , увеличиваемая
- 4. КредитыВыбирая кредитную программу, потенциальные заемщики ориентируются на
- 5. Дифференцированные платежи дают линейную зависимость от погашения
- 6. Теорема об аннуитетных платежах
- 7. Теорема о дифференцированных платежах.
- 8. Задача 1. По вкладу «А» банк начисляет
- 9. Слайд 9
- 10. Задача 2. Гражданин приобрел ценную бумагу за
- 11. Слайд 11
- 12. Задача 3.В июле планируется взять кредит на
- 13. РешениеиюльВыплаты февраль-июнь1234…89
- 14. Слайд 14
- 15. Задача 4. 31 декабря 2013г. Сергей взял
- 16. Решениеостаток на счетеначисление % 31 декабрявыплаты12340
- 17. Слайд 17
- 18. Слайд 18
- 19. 123…
- 20. Слайд 20
- 21. Слайд 21
- 22. Список литературы:1) Математика. ЕГЭ. Задача с экономическим
- 23. Скачать презентанцию
Простые проценты. Налоги.
Слайды и текст этой презентации
Слайд 3Сложные проценты. Вклады.
или
1) Величина S0 , увеличиваемая на p% в
течение n периодов в конце n-го этапа становится равной
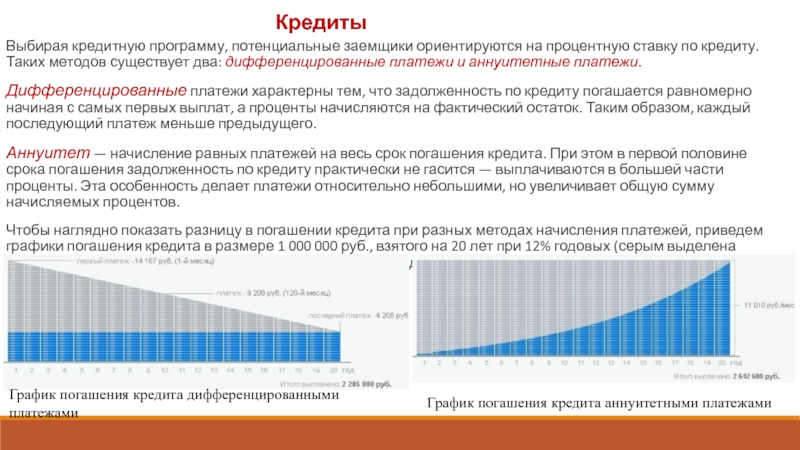
Слайд 4Кредиты
Выбирая кредитную программу, потенциальные заемщики ориентируются на процентную ставку по
кредиту. Таких методов существует два: дифференцированные платежи и аннуитетные платежи.
Дифференцированные
платежи характерны тем, что задолженность по кредиту погашается равномерно начиная с самых первых выплат, а проценты начисляются на фактический остаток. Таким образом, каждый последующий платеж меньше предыдущего.Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но увеличивает общую сумму начисляемых процентов.
Чтобы наглядно показать разницу в погашении кредита при разных методах начисления платежей, приведем графики погашения кредита в размере 1 000 000 руб., взятого на 20 лет при 12% годовых (серым выделена выплата процентов по кредиту, синим — выплата тела кредита).
График погашения кредита дифференцированными платежами
График погашения кредита аннуитетными платежами
Слайд 5Дифференцированные платежи дают линейную зависимость от погашения кредита: чем меньше
должен — тем меньше начислили процентов.
Сумма и срок досрочного
погашения ничем не ограничены. Досрочное погашение в аннуитетной схеме лишь сокращает срок выплаты кредита: на графике «срезаются» последние платежи и отпадает необходимость платить соответствующие им проценты, которые в конце графика как раз очень малы.
Таким образом, в аннуитетной схеме досрочное погашение невыгодно.
Кредиты
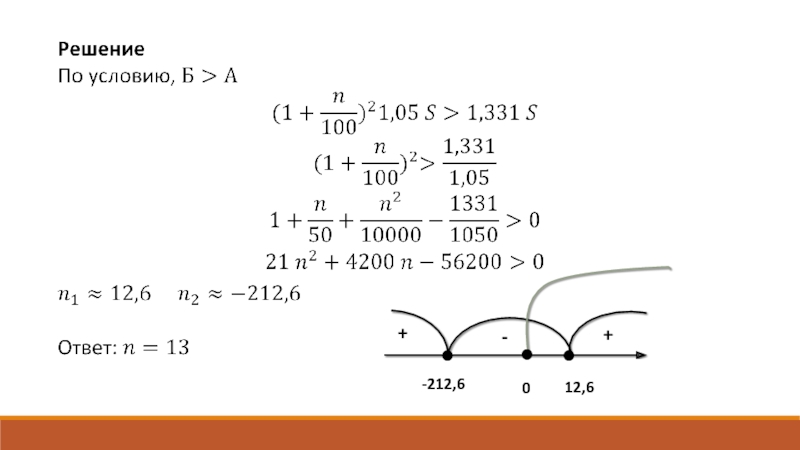
Слайд 8Задача 1. По вкладу «А» банк начисляет 10% каждый год,
а по вкладу «Б» - 5% в первый год и
n % за второй и третий годы. Найдите наименьшее целое значение n, при котором за 3 года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.Слайд 10Задача 2. Гражданин приобрел ценную бумагу за 7 тысяч рублей.
Цена бумаги возрастает каждый год на 2 тысячи рублей. В
любой момент гражданин может продать бумагу и положить вырученные деньги на банковский счет под 10% начислений в год. В течение какого года после покупки гражданин должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на банковском счете была наибольшей?Слайд 12Задача 3.В июле планируется взять кредит на сумму 4,5 млн
рублей сроком на 9 лет. Условия его возврата таковы:
- каждый
январь долг возрастает на n % по сравнению с концом предыдущего года;- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- каждый июль сумма долга должна отличаться от предыдущего на равную сумму.
Найдите целое число n, если наибольшая выплата за все время не превышает 1,4 млн рублей, а наименьшая выплата не менее 0,6 млн рублей.
Слайд 15Задача 4. 31 декабря 2013г. Сергей взял в банке 9 930 000
руб. в кредит под 10% годовых.
Схема выплаты кредита следующая:
31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какова должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Слайд 22Список литературы:
1) Математика. ЕГЭ. Задача с экономическим содержанием: учебно-методическое пособие.
/ под ред. Ф.ф.лысенко и с.ю.кулабухова, ростов-на-дону:легион, 2015. – 80с. 2)
ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов / под ред. и.в.ященко, издательство “национальное образование”, 2017 – 256с.3) Д.д.гущин, курс лекций по подготовке к егэ.
Веб-страница курса с актуальными материалами: http://reshuege.ru/course?id=2610 Издание 2, дополненное. — 05.04.2016