Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Задачи на построение"
Содержание
- 1. "Задачи на построение"
- 2. содержание занятия. Аннотация Аннотация
- 3. Аннотация Представленный проект рекомендован для учащихся 7
- 4. Цели урока: Образовательные.Изучение алгоритма решения задач
- 5. Задачи урока: 1. Организовать наблюдение за решением
- 6. Алгоритм решения задач на построение. В геометрических
- 7. Задачи на построение – это такие задачи,
- 8. Организоение за решением задачотрезок, равный данному В
- 9. Организоение за решением задачугол, равный данному В
- 10. Организоение за решением задачбиссектриса угла Чтобы разделить
- 11. середина отрезка Чтобы разделить данный отрезок AB
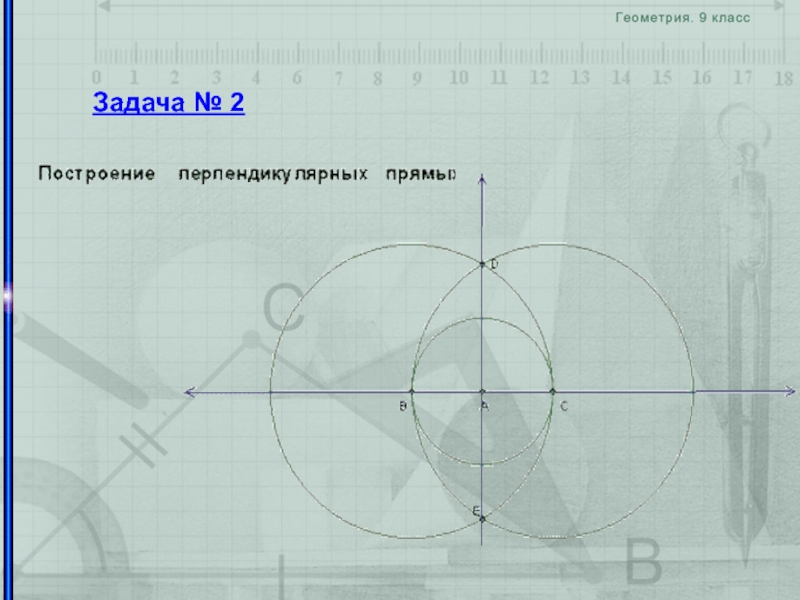
- 12. перпендикуляр к прямой
- 13. Организоение за решением задач2.Разделить данный отрезок пополам
- 14. физкульминутка ВЕТЕР ТИХО КЛЕН КАЧАЕТ,ВПРАВО, ВЛЕВО НАКЛОНЯЕТ,РАЗ – НАКЛОН,И ДВА – НАКЛОН,ЗАШУМЕЛ ЛИСТВОЮ КЛЕН.
- 15. перпендикуляр к прямой
- 16. Организоение за решением задачпрактическая работа
- 17. проверь себя
- 18. Домашнее задание Прочитать п. 23.Ответить на вопросы
- 19. Организоение за решением задачИз истории. Линейка считается
- 20. итоги урока Владеть алгоритмами решения основных задач
- 21. литература Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
- 22. спасибо, дети, за урок! БЛАГОДАРЮ ЗА ВНИМАНИЕ!!!
- 23. Автор проекта:
- 24. Задача №1
- 25. Задача № 2
- 26. Задача № 3
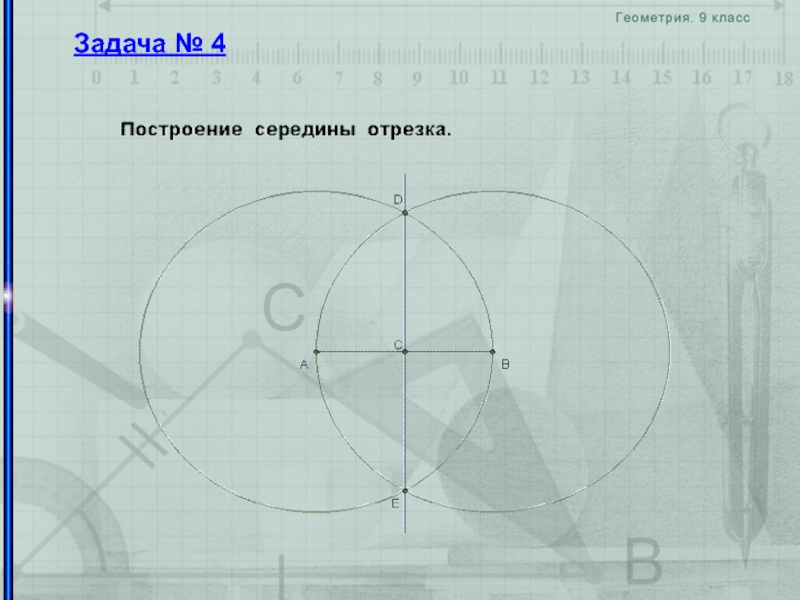
- 27. Задача № 4
- 28. 3. Построение треугольника по двум сторонам и
- 29. Слайд 29
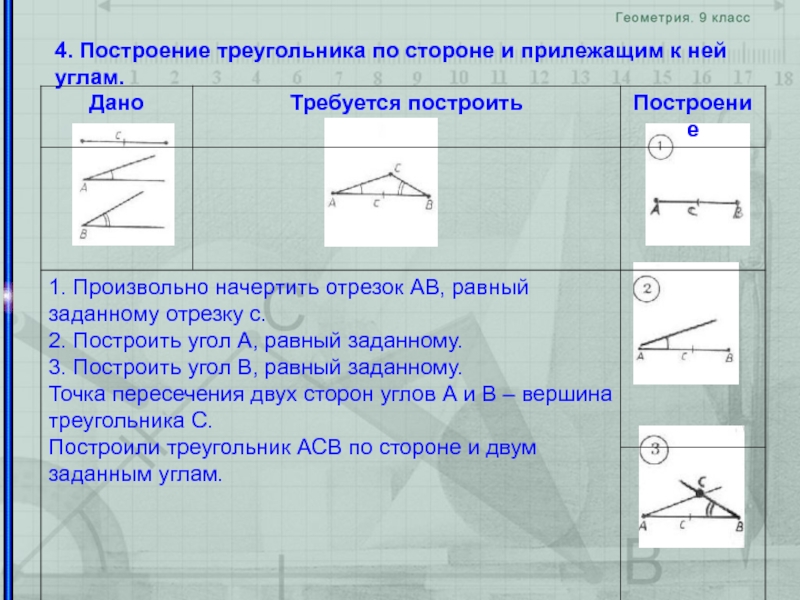
- 30. 4. Построение треугольника по стороне и прилежащим к ней углам.
- 31. Самостоятельная работа №2.Вариант 1Построить треугольник КМО, если
- 32. Построение треугольника по трем сторонам.
- 33. тест
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2содержание занятия.
Аннотация Аннотация
Цели урока
Аннотация Цели урока Задачи урокаИзучение нового материала:
Алгоритм решения задач на построение
Схема решения задач на построение
Построение: отрезка, равного данному; Построение: отрезка, равного данному; угла, равного данному; Построение: отрезка, равного данному; угла, равного данному; биссектрисы углаПостроение: отрезка, равного данному; угла, равного данному; биссектрисы угла; середины отрезкаПостроение: отрезка, равного данному; угла, равного данному; биссектрисы угла; середины отрезка; перпендикуляр к прямой.
Закрепление нового материала
Лабораторная работа
Физкультминутка
Практическая работа №1 в среде «Живая геометрия»
Практическая работа №2 в среде «Живая геометрия»
Проверь себя
Домашнее задание
Из истории.
Итог урока. Рефлексия.
Литература
Конец урока
Об авторе
Слайд 3Аннотация
Представленный проект рекомендован для учащихся 7 класса общеобразовательных школ,
лицеев, изучающих геометрию по учебнику для 7-9 классов общеобразовательных учреждений
под редакцией Л.С. Атанасяна и др.Проект разработан на основе образовательного комплекса 1С:Образование «Живая геометрия 3.1». Эффективность изучения темы достигается за счет использованию средств «Живой геометрии». Алгоритм решения задач на построение сопровождается соответствующим изменением чертежа. Учащиеся имеют возможность, изменяя длины данных отрезков и градусную меру угла, сделать вывод о возможных их значениях и убедиться в единственности существования: отрезка, равного данному; угла, равного данному; биссектрисы данного угла; перпендикуляра к прямой. Через систему пошаговых инструкций лабораторной работы реализуется принцип индивидуализации обучения. Наличие инструкций предоставляет выбор формы урока. Материал может быть изучен самостоятельно полностью или частично.
Слайд 4Цели урока:
Образовательные.
Изучение алгоритма решения задач на построение :
отрезка, равного данному; угла, равного данному; биссектрисы угла; деления отрезка
пополам; перпендикуляра к прямой.Применение этого алгоритма при решении конкретных задач с числовыми или геометрически заданными условиями.
Развивающие.
Развитие внимания, мышления (умения анализировать, делать выводы).
Формирование навыков исследовательской работы.
Формирование навыков самостоятельной работы, самоконтроля.
Воспитательные.
Воспитание интереса к предмету.
Воспитание таких качеств личности. как ответственность, аккуратность.
Слайд 5Задачи урока:
1. Организовать наблюдение за решением задач на
построение по алгоритму, включить школьников в активную работу над
построением.2. Стимулировать исследовательскую деятельность учащихся.
3. Использовать средства «Живой геометрии» для решения задач на построение.
4.Создать условия для самостоятельной работы учащихся.
Слайд 6Алгоритм решения задач на построение.
В геометрических построениях серединные перпендикуляры
приходится проводить очень часто, поэтому стоит обзавестись специальным инструментом ЖГ
для его построения. Мы предлагаем вам создать даже два таких инструмента. Первый должен рисовать серединный перпендикуляр к отрезку после указания курсором на сам отрезок (концы отрезка при этом не используются и могут быть скрыты; рис. 1). Второй, наоборот, рисует серединный перпендикуляр к отрезку AB после указания курсором концов A и B отрезка (при этом самого отрезка на картинке может и не быть; рис. 2). Постройте инструменты по-разному: первый – используя команды «Середина отрезка» и «Перпендикуляр» меню «Построение»; второй – используя только «Циркуль» и «Линейку» «Живой геометрии».
А теперь перейдите в окно ЖГ, чтобы выполнить эти задания. Там же – пример применения ваших инструментов.
Слайд 7Задачи на построение – это такие задачи, при решении которых
нужно построить геометрическую фигуру, удовлетворяющую условиям задачи, с помощью циркуля
и линейки без делений.Анализ (рисунок искомой фигуры, устанавливающий связи между данными задачи и искомыми элементами, и план построения).
Построение по намеченному плану.
Доказательство, что данная фигура удовлетворяет условиям задачи.
Исследование (при любых ли данных задача имеет решение, и если имеет, то сколько).
схема решения задач на построение
Слайд 8Организоение за решением задач
отрезок, равный данному
В кружках на рисунках
показан порядок построения. В данном задании отрезок можно построить в
три этапаПровести луч с началом в точке А1;
3. Провести часть окружности, радиус которой
равен отрезку АВ, с центром в точке А1. Точка пересечения
окружности и луча дадут точку В1.
4.Построен отрезок АВ1, равный отрезку АВ.
Слайд 9Организоение за решением задач
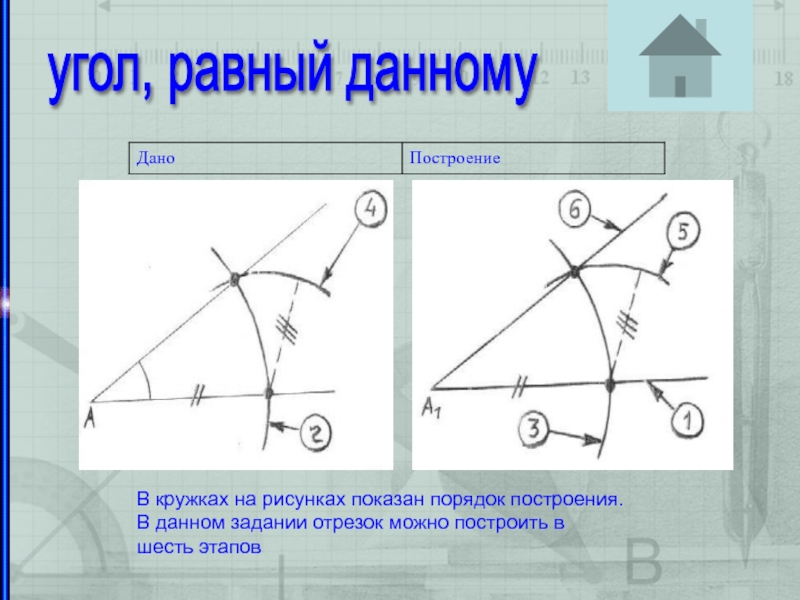
угол, равный данному
В кружках на рисунках
показан порядок построения. В данном задании отрезок можно построить в
шесть этапов
Слайд 10Организоение за решением задач
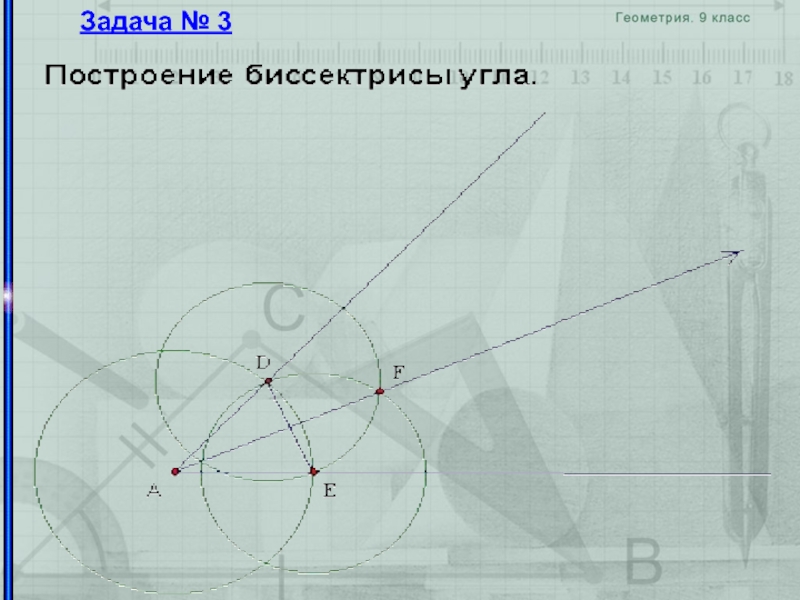
биссектриса угла
Чтобы разделить угол AOB пополам,
строим окружность w(O,r)до пересечения со сторонами в точках A' и
B', а затем строим окружности w(A',r) и w(B',r). Две последние окружности пересекаются в точках O и O', и OO' – биссектриса угла AOB.Чтобы разделить угол с вершиной O пополам, строим произвольную окружность w с центром O, а затем окружности того же радиуса с центрами в точках пересечения w со сторонами (они просто проходят через O); вторая точка их пересечения P лежит на биссектрисе. Остается провести луч OP.
Слайд 11середина отрезка
Чтобы разделить данный отрезок AB пополам, проводим пересекающиеся
окружности w(A,r), w(B,r) (одинакового радиуса) и соединяем точки их пересечения
C и C'. Точка пересечения CC' и AB – искомая точка.Чтобы разделить данный отрезок AB пополам, проводим пересекающиеся окружности w(A,r), w(B,r) и строим точку пересечения их общей хорды CD с отрезком AB – она и будет искомой серединой.
Слайд 13Организоение за решением задач
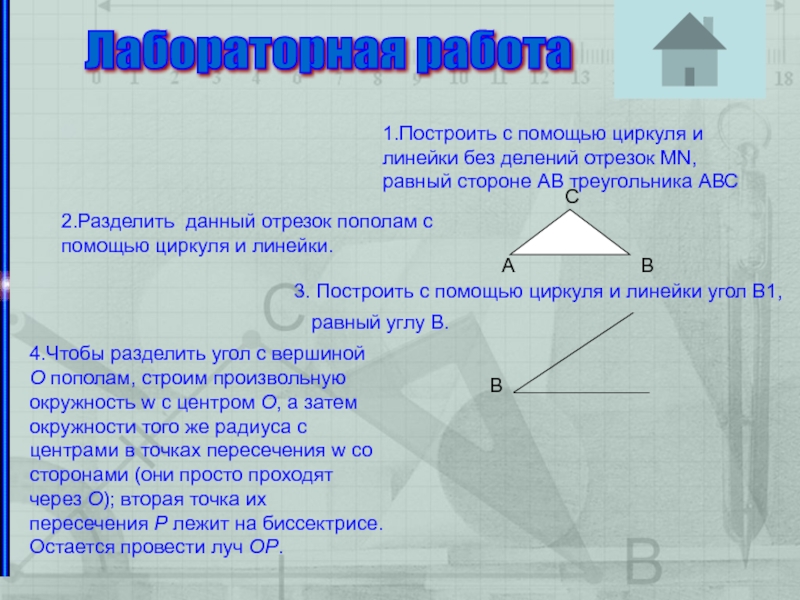
2.Разделить данный отрезок пополам с помощью циркуля
и линейки.
1.Построить с помощью циркуля и линейки без делений отрезок МN, равный стороне АВ треугольника АВС
3. Построить с помощью циркуля и линейки угол В1,
равный углу В.
В
4.Чтобы разделить угол с вершиной O пополам, строим произвольную окружность w с центром O, а затем окружности того же радиуса с центрами в точках пересечения w со сторонами (они просто проходят через O); вторая точка их пересечения P лежит на биссектрисе. Остается провести луч OP.
Лабораторная работа
А
В
С
Слайд 14физкульминутка
ВЕТЕР ТИХО КЛЕН КАЧАЕТ,
ВПРАВО, ВЛЕВО НАКЛОНЯЕТ,
РАЗ – НАКЛОН,
И ДВА
– НАКЛОН,
ЗАШУМЕЛ ЛИСТВОЮ КЛЕН.
Слайд 18Домашнее задание
Прочитать п. 23.
Ответить на вопросы 17; 18; 19;
20;21 стр. 50.
Решить задачу № 180; № 185.
Составить алгоритм построения
треугольника по двум сторонам и углу, заключенному между ними
Слайд 19Организоение за решением задач
Из истории.
Линейка считается не имеющей делений
и лишь с одним прямолинейным краем – с ее помощью, имея
на плоскости две точки, A и B, можно провести прямую AB. Никаких других построений с помощью линейки делать нельзя (скажем, нельзя приложить ее к двум окружностям и провести их общую касательную).Циркуль предназначен для единственной цели – если на плоскости заданы отрезок AB и точка O, то с помощью циркуля можно провести окружность с центром O радиуса R = AB.
Название «циркуль» позднего происхождения – оно происходит от лат. circulus – круг.
«Линейка» также происходит от лат. linea, linum – лен, льняная нить.
Задачи на построение вошли в практику задолго до того, как геометрия и вообще математика стала настоящей теоретической наукой. И в Вавилоне, и в Древнем Египте в IV–II тысячелетиях до н.э. уже существовала практическая математика (в виде правил записи чисел, т. е. системы счисления, и правил различных вычислений), и практическая геометрия – геометрия в изначальном смысле слова: измерение земли. Но и при измерениях, и при строительных работах нужны были построения.
Слайд 20итоги
урока
Владеть алгоритмами решения основных задач на построение.
РЕФЛЕКСИЯ:
1.Научился
ли ты строить угол, равный данному?
2.Сумеешь ли ты построить перпендикуляр
к прямой?3.Знаешь ли ты, как построить середину отрезка?
4.Сможешь ли ты построить биссектрису угла?
5.Сколько шагов необходимо, чтобы построить отрезок, равный данному?
6.Больше всего мне понравилось………
7.Трудности возникли при построении…….
8.Хотелось ли бы тебе узнать другую тему с помощью «Живой геометрии»
И.И.Александров: «Искусство решать задачи на построение слагается главным образом из уменья читать чертежи, из находчивости в проведении вспомогательной линии и, наконец, равным образом, из знания и уменья применять методы».
Слайд 21литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и другие. Геометрия:
учебник для 7-9 классов общеобразовательных учреждений. М: Просвещение 2002 г.
Атанасян
Л. С., Бутузов В.Ф., Глазков Ю.А. и др. Изучение геометрии в 7, 8, 9 классах: Методические рекомендации к учебнику: Кн. Для учителя. М: Просвещение 2003 г.Математика, 5- 11 классы Практикум-1С: Образование, «Живая геометрия
Слайд 23Автор проекта:
Кудоспаева Надежда Николаевна,
учитель высшей
квалификационной категории, МБОУ - Средняя общеобразовательная школа № 1
Слайд 29
Самостоятельная работа №1.
Вариант 1. Построить треугольник ВСН, если ВС = 3 см, СН = 4 см, ∟С = 35° Вариант 2. Построить треугольник СДЕ, у которого ДС = 4 см, ДЕ = 5 см, ∟Д = 110°
Подсказка. Перед построением треугольника необходимо сделать «от руки» чертеж треугольника, где показаны все заданные элементы.
Слайд 31Самостоятельная работа №2.
Вариант 1
Построить треугольник КМО, если КО = 6
см, ∟К = 130°, ∟О = 20°.
Вариант 2
Построить треугольник ВСР,
если ∟С = 15°, ∟Д = 50°, СД = 3 см.Самостоятельная работа №3.
Вариант 1. Построить треугольник ОДЕ, если ОД = 4 см, ДЕ = 2 см, ЕО = 3 см.
Вариант 2 Построить треугольник МНО, если МН = 1 см, НО = 4 см, ОМ = 3 см.
После построения любого треугольника, самостоятельно провести доказательство того, что получившийся треугольник – искомый, и по возможности провести исследование.