Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Жизнь и творчество Леонардо Эйлера
Содержание
- 1. Жизнь и творчество Леонардо Эйлера
- 2. Содержание. 1. Вступление 2. Периоды жизни. 3.
- 3. Слайд 3
- 4. Трудно даже перечислить все отрасли, в которых
- 5. 2. Периоды жизни.15 апреля 1707 года, родился
- 6. 2. Периоды жизни.30 апреля 1766 года. Эйлер
- 7. 3. Окружность Эйлера
- 8. Теорема Основания высот, основании медиан
- 9. Прежде чем приступить кдоказательству этой теоремы, обратим
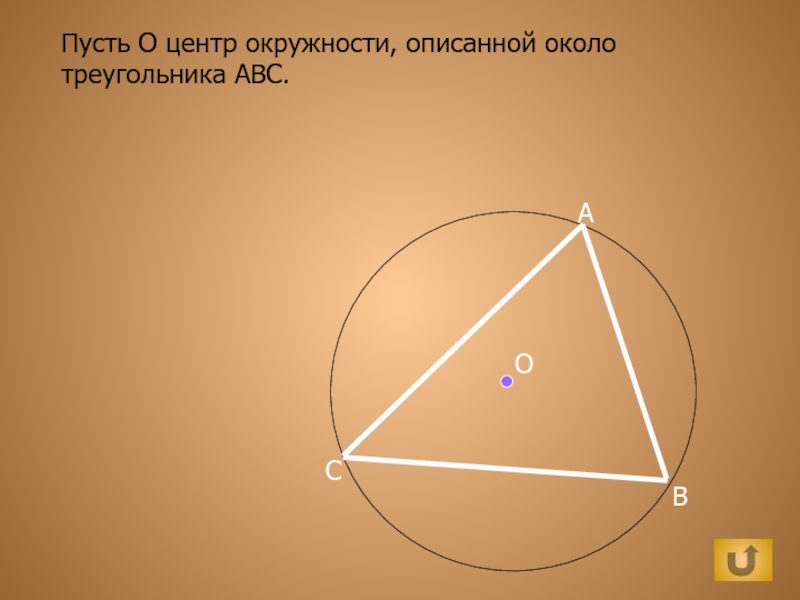
- 10. Пусть О центр окружности, описанной около треугольника ABC.ОАBC
- 11. ОМ – точка пересечения его медианМABC
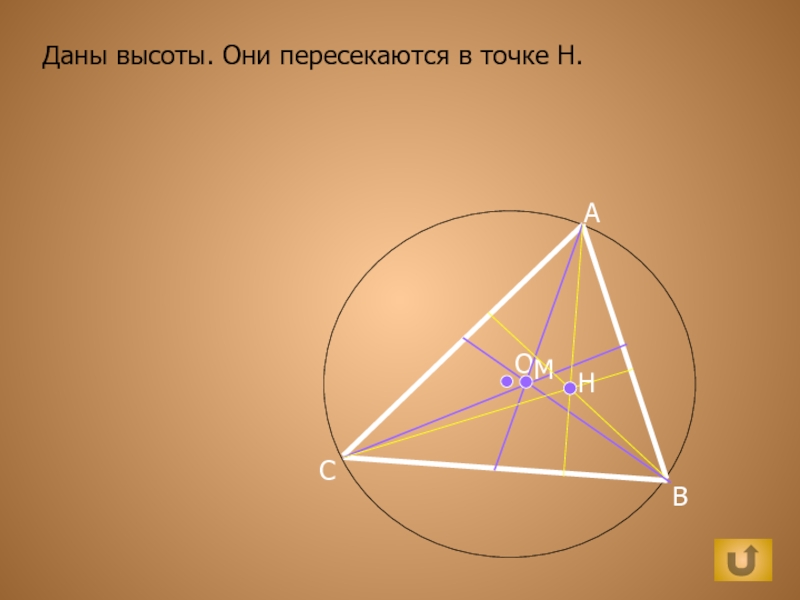
- 12. ОМABCДаны высоты. Они пересекаются в точке H.H
- 13. ОМABCH Вводится не вписанная окружность на которой находятся
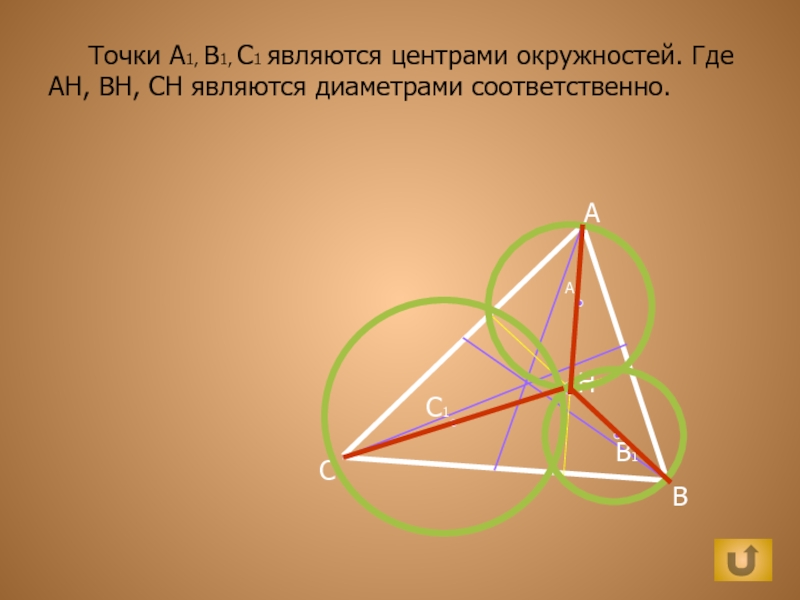
- 14. ABCHC1A1B1 Точки A1, B1, C1 являются центрами окружностей. Где АН, ВН, СН являются диаметрами соответственно.
- 15. Основания высот обозначим А2, В2, С2 соответственно.ABCHА2В2С2
- 16. Треугольники АВ2С2, А2ВС2, А2В2С подобны между собой и подобны исходному треугольнику АВС.ABCHА2В2С2
- 17. ABCHА2В2С2 Пусть А, В и С величины углов треугольника АВС.
- 18. ОМABCHC1A1B1Пусть А3, В3, С3 основания медиан.А3В3С3Расстояние от
- 19. Прямая Эйлера.Из прошлого утверждения (|A3O|=|AH|\2, |B3O|=|BH|\2, |C3O|=|CH|\2)
- 20. BCC1A1B1А3В3С3AВ2А2С2 Докажем теперь, что точки А1, В2, В3,
- 21. BCА3В3AА2С2Сначала заметим что точки В3, А3, А2,
- 22. BCC1A1B1А3В3С3AВ2А2С2С другой стороны, если мы рассмотрим четырехугольник
- 23. 5. Применение свойств окружности Эйлера и прямой
- 24. Задача 3. В треугольнике ABC проведена медиана АА1
- 25. 6. Литература1. Глейзер Г.И. История математики в
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Содержание.
1. Вступление
2. Периоды жизни.
3. Окружность Эйлера
4.
Прямая Эйлера.
5. Применение свойств окружности Эйлера и прямой Эйлера.
6. ЛитератураСлайд 3
Леонард Эйлер — математик, физик, механик и астроном. Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику по руководствам, первыми образцами которых явились классические монографии Эйлера. Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук.
1. ВСТУПЛЕНИЕ
Слайд 4 Трудно даже перечислить все отрасли, в которых трудился великий учёный.
Евклидова
геометрия
Точки Эйлера,
Прямая Эйлера,
Окружность Эйлера.
Теория графов
Решение задачи о семи
мостах Кёнигсберга
Топология
Формула Эйлера для многогранников.
Вычислительная математика
метод ломаных Эйлера, один из простейших методов приближённого решения дифференциальных уравнений, широко применявшийся до самых последних лет;
Комбинаторика
Метод производящих функций.
Математический анализ
Формула Эйлера
Эйлеровы интегралы: бета-функция и гамма-функция Эйлера.
Механика
Уравнения Эйлера, описывающими движение невязкой среды.
Углы Эйлера при описании движения тел.
Инженерное дело
Эвольвентный профиль в зубчатых передачах.
Слайд 52. Периоды жизни.
15 апреля 1707 года, родился Леонардо Эйлер.
20 октября
1720 года, Эйлер стал студентом факультета искусств Базельского университета.
4 июня
1724 года, Эйлер произнёс по латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона — и был удостоен учёной степени магистра.5 апреля 1727 года, Эйлер навсегда покидает Швейцарию, по совету братьев Бернулли его пригласили стать адъюнктом по физиологии в Санкт-Петербурге.
1733 год. 26-летний Леонард Эйлер женился на дочери живописца Екатерине Гзель, которой в это время тоже было 26 лет.
1736 год. Издано двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении».
1741 год. В соответствии с поданным Эйлером прошением, он был «отпущен от Академии» и утверждён почётным академиком. Он обещал по мере своих сил помогать Петербургской Академии — и действительно помогал весьма существенно все 25 лет, пока не вернулся обратно в Россию. В июне 1741 г. Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками прибыл в Берлин.
1757 год. Эйлер впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Однако в те годы эти формулы не могли найти практического применения.
Леонардо Эйлер
Слайд 62. Периоды жизни.
30 апреля 1766 года. Эйлер получает разрешение на
выезд из Берлина в Россию.
1771 год. Сгорела библиотека со множеством
трудов Леонардо Эйлера, но в течении некоторого времени Эйлер восстанавливает утраченные труды по памяти. В сентябре того же года в Санкт-Петербург прибыл известный немецкий окулист барон Венцель, который согласился сделать Эйлеру операцию — и удалил с левого глаза катаракту. Но вся операция заняла 3 минуты — и Эйлер снова стал видеть! Искусный окулист предписал беречь глаз от яркого света, не писать, не читать — лишь постепенно привыкать к новому состоянию. Эйлер нарушил эти наставления и на следующий день начал писать свои труды дальше, окончательно потеряв зрение.1773 год. Умерла жена Эйлера.
В сентябре 1783 г. учёный стал ощущать головные боли и слабость. 7 сентября после обеда, проведённого в кругу семьи, беседуя с А. И. Лекселем об недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести «Я умираю» — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг. «Эйлер перестал жить и вычислять». Его похоронили на Смоленском кладбище в Петербурге. Надпись на памятнике гласила: «Леонарду Эйлеру — Петербургская Академия».
Надгробие Л. Эйлера. Гранитный саркофаг. 1837 г.
Слайд 73. Окружность Эйлера
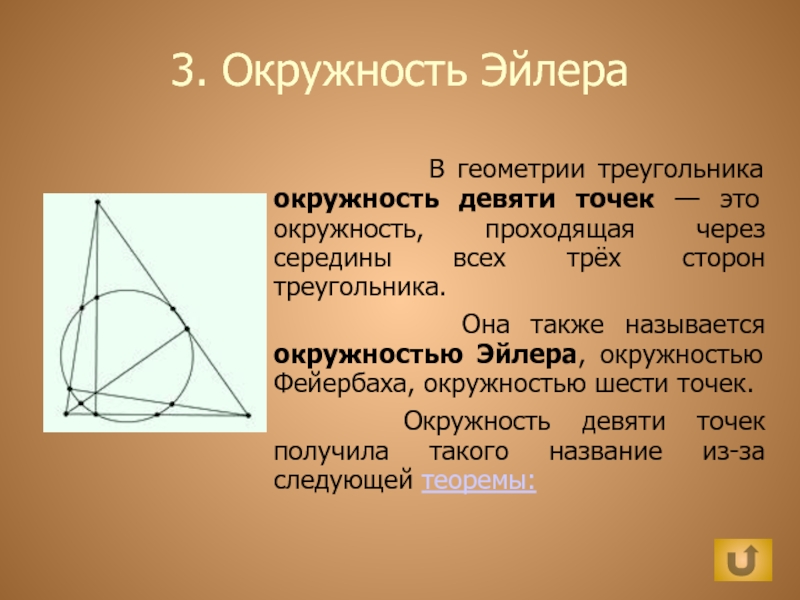
В геометрии
треугольника окружность девяти точек — это окружность, проходящая через середины
всех трёх сторон треугольника.Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек.
Окружность девяти точек получила такого название из-за следующей теоремы:
Слайд 8
Теорема
Основания высот, основании медиан и
точки, расположенные на
серединах отрезков
от ортоцентра (точка пересечения высот) до
вершин ттреугольника, лежат
на однойокружности.
Слайд 9 Прежде чем приступить к
доказательству этой теоремы, обратим внимание на несколько
простых, но полезных фактов, связанных с геометрией треугольника
Слайд 13
О
М
A
B
C
H
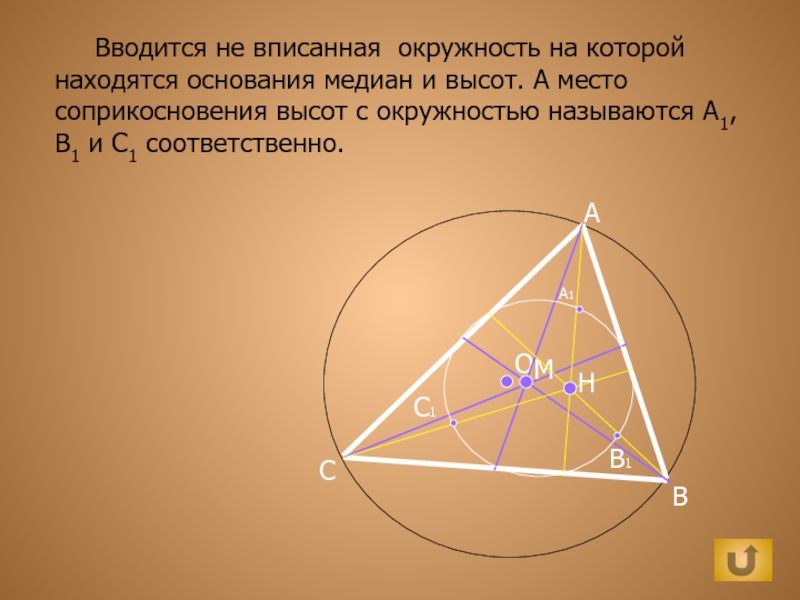
Вводится не вписанная окружность на которой находятся основания медиан и
высот. А место соприкосновения высот с окружностью называются A1, B1
и C1 соответственно.C1
A1
B1
Слайд 14
A
B
C
H
C1
A1
B1
Точки A1, B1, C1 являются центрами окружностей. Где АН, ВН,
СН являются диаметрами соответственно.
Слайд 16 Треугольники АВ2С2, А2ВС2, А2В2С подобны между собой и подобны исходному
треугольнику АВС.
A
B
C
H
А2
В2
С2
Слайд 18
О
М
A
B
C
H
C1
A1
B1
Пусть А3, В3, С3 основания медиан.
А3
В3
С3
Расстояние от точки О до
каждой стороны треугольника…
Вдвое меньше чем расстояние от противоположной вершины до
ортоцентраНа рисунке видно, что ОА3 в два раза меньше АН, следовательно |A3O|=|AH|\2, |B3O|=|BH|\2, |C3O|=|CH|\2
Слайд 19Прямая Эйлера.
Из прошлого утверждения (|A3O|=|AH|\2, |B3O|=|BH|\2, |C3O|=|CH|\2) следует, что точки
О, М, Н лежат на одной прямой.
Поскольку прямая ОН делит
медиану АА3 в том же отношении что и точка М эта прямая носит название «Прямая Эйлера»Легко видеть, что |OM|= |ОН|\2
О
М
B
C
H
C1
A1
B1
А3
В3
С3
A
Слайд 20B
C
C1
A1
B1
А3
В3
С3
A
В2
А2
С2
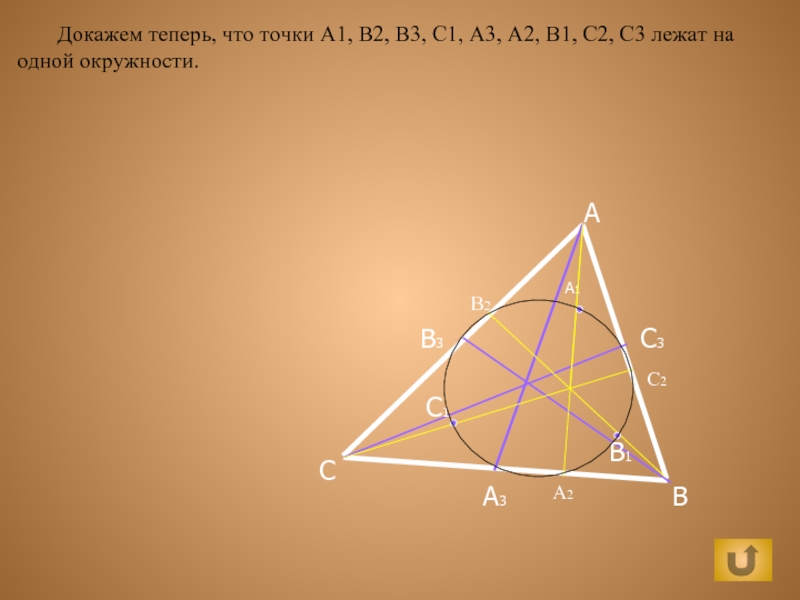
Докажем теперь, что точки А1, В2, В3, С1, А3, А2,
В1, С2, С3 лежат на одной окружности.
Слайд 21B
C
А3
В3
A
А2
С2
Сначала заметим что точки В3, А3, А2, С2 лежат на
одной окружности поскольку В3А2 и С2А2 медианы прямоугольных треугольников АА2С
и АА2В проведенных на гипотенузы, и следовательно,<В3А2С2=
С3
Таким образом шесть точек лежат на окружности А2, В2, С3, А3, В3, С2.
В2
Слайд 22B
C
C1
A1
B1
А3
В3
С3
A
В2
А2
С2
С другой стороны, если мы рассмотрим четырехугольник А1В1А3С1 и выразим
какие то два его угла через углы А, В, С
мы убедимся, что их сумма равна 180°.Отсюда следует что четырехугольник А1В1А3С1 вписанный. Таким образом, шесть точек А1, В1, С1, А3, В3, С3 также лежат на одной окружности.
Значит все девять точек А1, В1, С1, А2, В2, С2, А3, В3, С3 лежат на одной окружности.
Теорема Эйлера доказана.
Слайд 235. Применение свойств окружности Эйлера и прямой Эйлера.
Задача 1
Доказать,
что радиус окружности, проведенной через две
вершины ортоцентр непрямоугольного треугольника,
равен радиусу окружности, описанной около этого треугольника.
Решение при помощи свойств окружности Эйлера или при помощи симметрии).
Задача 2.
Точка О1 симметрична центру О описанной около
треугольника АBC окружности относительно стороны BC.
Докажите, что прямая Эйлера треугольника ABC проходит через
середину отрезка АО1.
Решение по свойству точки пересечения медиан.
Слайд 24Задача 3.
В треугольнике ABC проведена медиана АА1 и высоты ВВ2
и СС2.
Докажите, что касательная к описанной около него окружности
в точкеА и касательная к его окружности Эйлера в точке А1 и прямая В2С2
параллельны друг другу. (решение при помощи подобия и свойств
окружности Эйлера).
Ряд задач нами составлен самостоятельно.
Задача 4.
В окружность Эйлера треугольника АВС вписан треугольник,
подобный данному. Сторона ВС = a см. Найти сходственную сторону
этого вписанного треугольника.
Решение при помощи свойств окружности Эйлера и центрального подобия.
Задача 6.
Дан неравносторонний треугольник АВС и описанная вокруг него
окружность, а также треугольник А1В1С1 , вершина которого лежит в центре
описанной окружности, а ортоцентр треугольника АВС является серединой
противолежащей стороны А1В1С1. Доказать, что точки пересечения медиан этих
треугольников АВС или совпадают, или симметричны относительно центра
окружности Эйлера.
Решение при помощи свойств прямой Эйлера и свойств точки пересечения медиан.
Слайд 256. Литература
1. Глейзер Г.И. История математики в школе IX–X классы
– М.; Просвещение, 1983.
2. Замечательные ученые. Под ред. Капицы С.П.
– М.; издательство «Наука», 1980.3. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005.
4. Стройк Д.Я. Краткий очерк Истории математики. – М.; издательство «Наука», 1969.
5. Юшкевич Ф.П. История математики в России. – М.; издательство «Наука», 1968.
6. Яковлев А.Я. Леонард Эйлер. – М.; Просвещение, 1983