§ 8. ЗАКОНЫ ДВИЖЕНИЯ ПЛАНЕТ СОЛНЕЧНОЙ СИСТЕМЫ

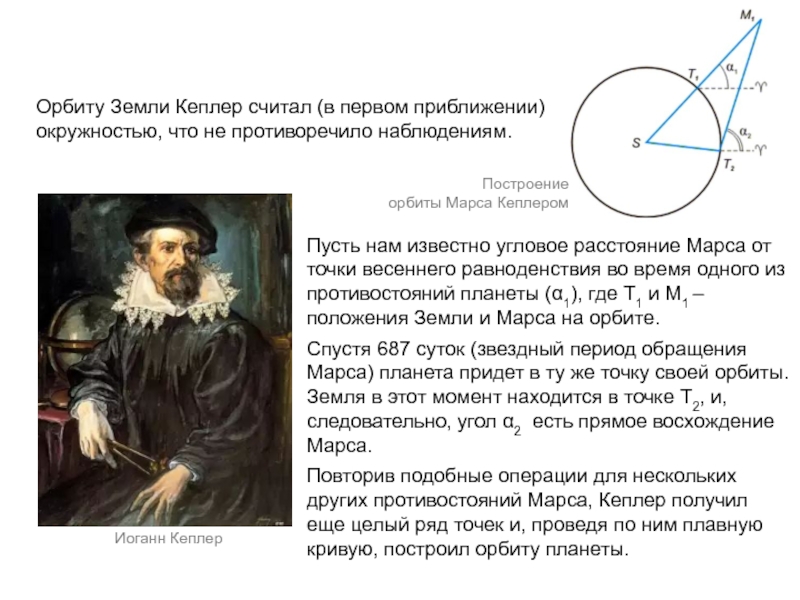
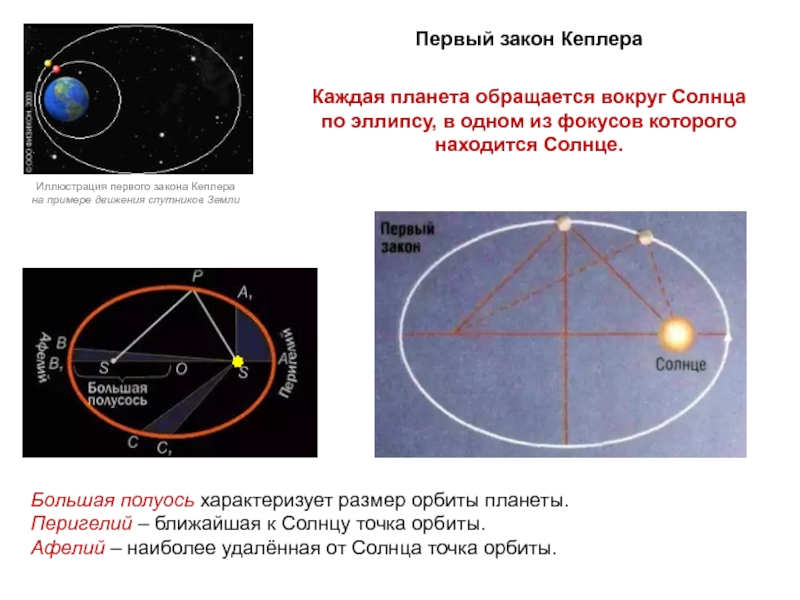
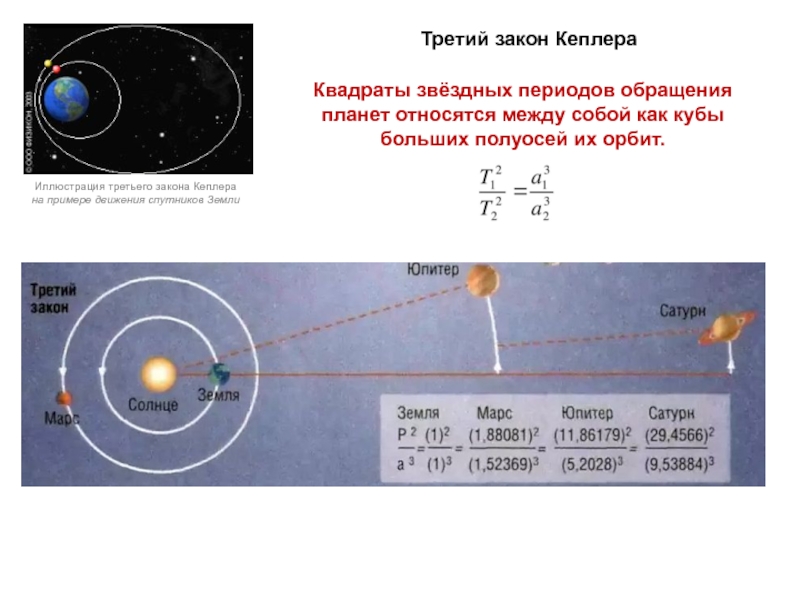
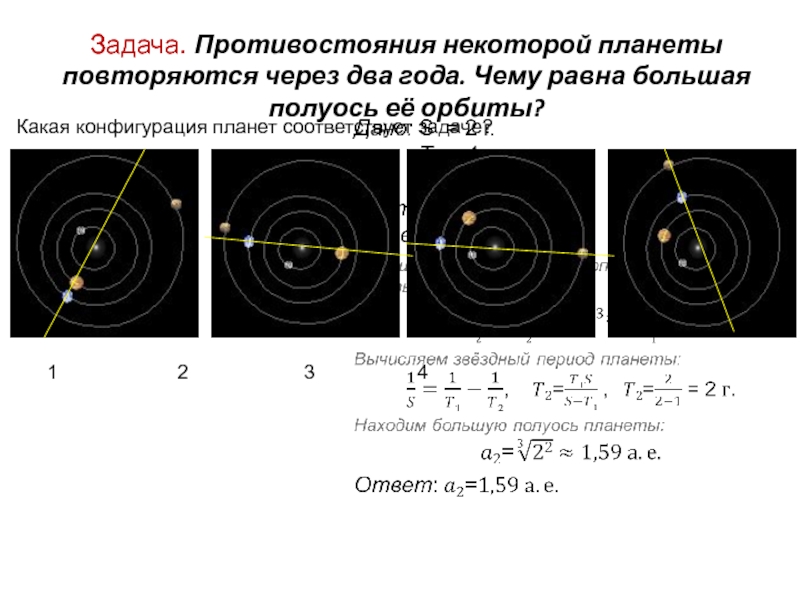
небесных тел должно быть равномерным и происходить по «самой совершенной»

кривой – окружности.

Иоганн Кеплер

Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.
В своих поисках Кеплер ис­ходил из убеждения, что «в мире правит число», высказанного еще Пифагором. Он искал соотно­шения между различными величи­нами, характеризующими движе­ние планет, — размеры орбит, период обращения, скорость.
Кеп­лер действовал фактически всле­пую, чисто эмпирически.

а также многолетними определениями координат и конфигураций Марса, проведёнными его

учителем Тихо Браге.

Иоганн Кеплер

не противоречило наблюдениям.
Построение
орбиты Марса Кеплером
Пусть нам известно угловое расстояние

Марса от точки весеннего равноденствия во время одного из противостояний планеты (α1), где Т1 и М1 –
положения Земли и Марса на орбите.
Спустя 687 суток (звездный период обращения Марса) планета придет в ту же точку своей орбиты. Земля в этот момент находится в точке Т2, и, следовательно, угол α2 есть прямое восхождение Марса.
Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил еще целый ряд точек и, проведя по ним плавную кривую, построил орбиту планеты.

не противоречило наблюдениям.
В ходе построения орбиты планеты Марс Кеплер был

поставлен перед необходимостью сделать выбор одного из двух возмож­ных решений:
считать, что орбита Марса представляет со­бой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с на­блюдениями (из-за ошибок наблюдений) на 8';
считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью.
Будучи уверенным в точности наблюдений Ти­хо Браге, Кеплер выбрал второе решение.

называется эллипсом, при этом Солнце не располагается в центре эллипса.
Эллипс

– кривая, у которой сумма расстояний от любой точки до его фокусов есть величина постоянная.

Иоганн Кеплер

планета обращается вокруг Солнца
по эллипсу, в одном из фокусов

которого находится Солнце.

Первый закон Кеплера

Большая полуось характеризует размер орбиты планеты.
Перигелий – ближайшая к Солнцу точка орбиты.
Афелий – наиболее удалённая от Солнца точка орбиты.

площади.
Иллюстрация второго закона Кеплера
на примере движения спутников Земли
По

мере приближения планеты к Солнцу возрастает ее скорость – увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.

Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии.

звёздных периодов обращения планет относятся между собой как кубы больших

полуосей их орбит.

Третий закон Кеплера

наконец найдено, и это открытие превзошло все мои самые

смелые ожидания...»
Иоганн Кеплер

Третий закон позволяет вычислить относительные расстояния планет от Солнца, используя при этом уже известные периоды их обращения вокруг Солнца.
Не нужно определять расстояние от Солнца каждой из них, достаточно измерить расстояние от Солнца хотя бы одной планеты.
Величина большой полуоси земной орбиты – астрономическая единица (а.е.) – стала основой для вычисления всех остальных расстояний в Солнечной системе.

большая полуось её орбиты?
1 2

3 4

Какая конфигурация планет соответствует задаче?