1. Электрохимическая кинетика. Электрохимические системы в неравновесном

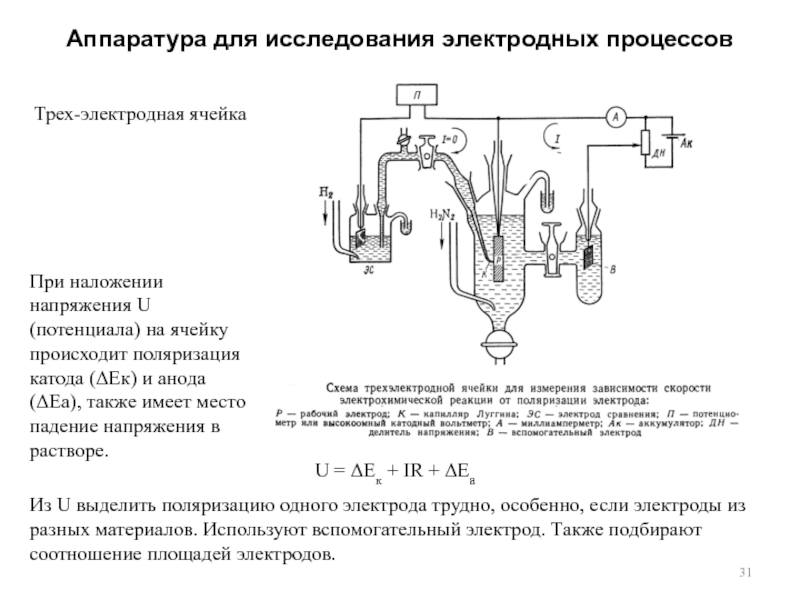
процессов. Собственно электродная реакция или стадия разряда-ионизации. Процессы, сопутствующие электродной

реакции. Процессы, осложняющие электродную реакцию.
2. Кинетика электродных процессов. Факторы, оказывающие влияние на кинетику электродных процессов.
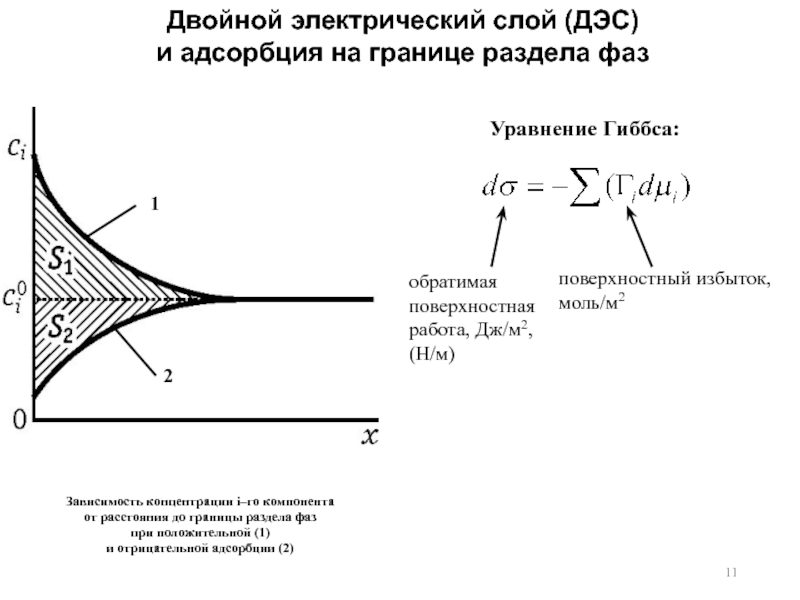
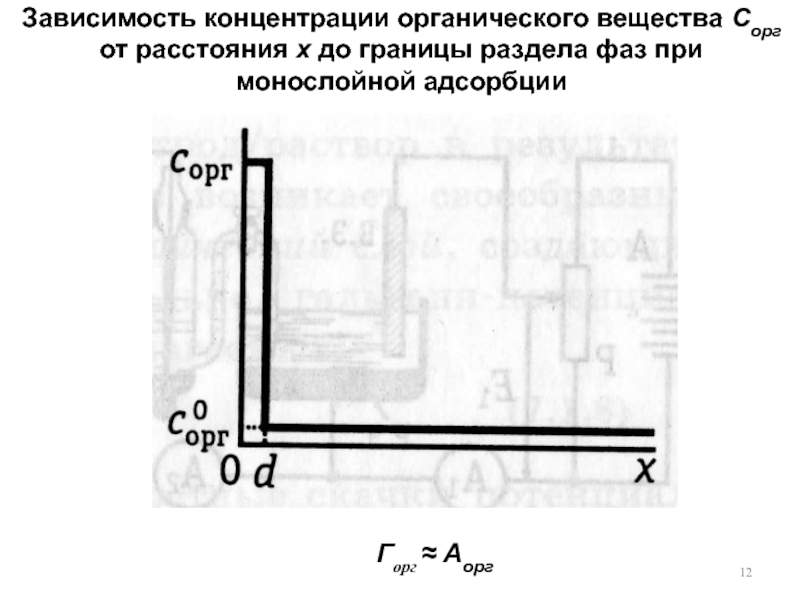
3. Двойной электрический слой (ДЭС). Причина возникновения. Примеры проявления. Потенциал нулевого заряда. Методы изучения ДЭС. Емкость ДЭС.
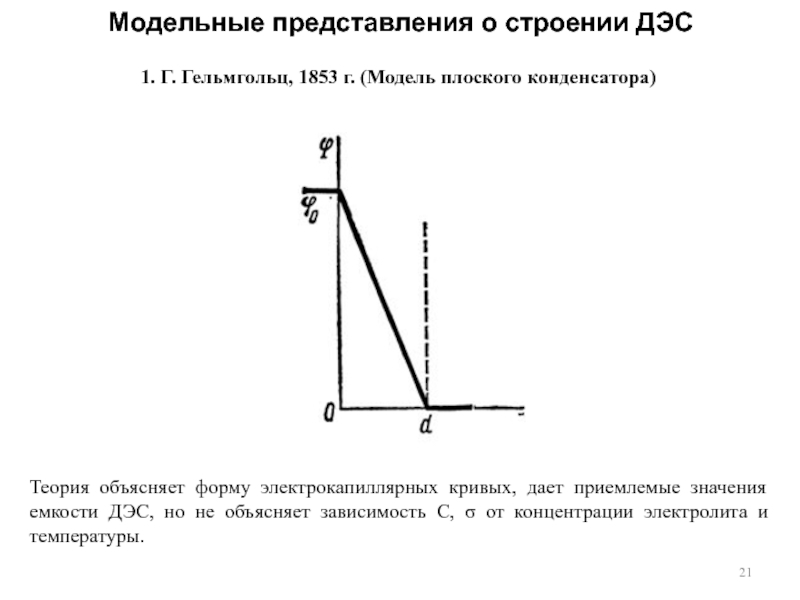
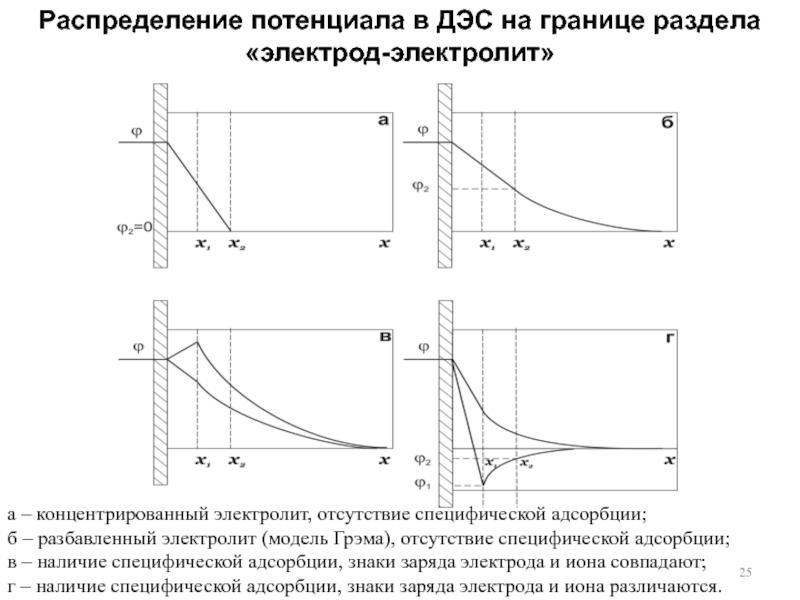
4. Структура ДЭС. Модель Гельмгольца. Модель Гуи-Чапмена. Модель Штерна. Модель Грэма.
5. Кинетические закономерности стадии разряда-ионизации. Катодные процессы, анодные процессы. Фарадеевские токи и токи заряжения. Поляризация и перенапряжение. Система знаков.

процесса
Массоперенос продукта

гетерогенного переноса электрона. Элементарный акт взаимодействия ē с окисленной формой

или переход ē от восстановленной формы на электрод.
Процессы, сопутствующие гетерогенному переносу электрона. Стадии массопереноса.
- Доставка реагентов в реакционную зону.
- Отвод продуктов из реакционной зоны.
Диффузия, миграция и конвекция.
Процессы, осложняющие электродную реакцию
Предшествующая или последующая химическая реакция в объеме раствора.
+n ē
A → O → R → B
Образование новой фазы.
Адсорбция на поверхности электрода.
Влияние структуры границы раздела между электродом и раствором на скорость процессов (строение ДЭС).

Стадии электродного процесса

происходит выделение водорода на катоде и кислорода на аноде. Площади

электродов равны 1 см2.
Минимальная разность потенциалов, необходимая для такого процесса равна 1,23 В. Об этом говорит термодинамика равновесных процессов. Но она не говорит о скорости его выделения.
На ртути при таком потенциале с 1 см2 выделится при 25С 1 мл водорода только через 4·105 лет.
При увеличении разности потенциалов до 3,5 В, выделение водорода происходит с видимой скоростью 7 см3/мин. Но КПД=1,23*100/3,5=35%
Используя специальным образом подготовленный платиновый электрод скорость удается повысить в 109 раз!
Александр Наумович Фрумкин: «Теории двойного слоя, массопереноса и элементарного акта – это те «три кита», на которых базируется здание кинетики электродных процессов.»

1 рода.

Ртуть в растворе поверхностно-неактивного электролита, например, NaF. Идеально поляризуемый

электрод.

Ртуть (идеально поляризуемый электрод) в растворе поверхностно-активного электролита, например, KI.

Ртуть (идеально поляризуемый электрод) в водном растворе в присутствии поверхностно-активных полярных молекул органического вещества, например, н-бутилового спирта при потенциале нулевого заряда.

Зависимость концентрации i–го компонента
от расстояния до границы раздела фаз

при положительной (1)
и отрицательной адсорбции (2)

1

2

Уравнение Гиббса:

обратимая поверхностная работа, Дж/м2, (Н/м)

поверхностный избыток, моль/м2

раздела фаз при монослойной адсорбции
Горг  Аорг

электрод. Весь подводимый заряд затрачивается только на изменение свободного заряда

электрода, компенсируемого адсорбцией ионов.

E< Eq=0 → Г+ > 0 и Г- < 0

E>Eq=0 → Г+ < 0 и Г- > 0

Условие электронейтральности:

q = -FГ+ + FГ-

q – заряд электрода, приходящийся на единицу поверхности;
F- постоянная Фарадея.



емкость ДЭС

ПНЗ Eq=0 = 0 Г+ = Г- = 0

Адсорбция приводит к пространственному разделению зарядов. На границе электрод/раствор в результате электростатической адсорбции ионов возникает своеобразный микроконденсатор – двойной электрический слой, создающий разность потенциалов Δφ.

KI. Специфическая адсорбция.

ПНЗ Eq=0 = 0 z+Г+ = z-Г-  0
Распределение

катионов (1) и анионов (2) у поверхности незаряженного электрода при специфической адсорбции.

IV. Ртуть (идеально поляризуемый электрод) в водном растворе в присутствии поверхностно-активных полярных молекул органического вещества, например, н-бутилового спирта при п.н.з.

Бутиловый спирт адсорбируется на незаряженной поверхности так, что к поверхности ртути направлен радикал C4H9 а в раствор – гидроксильная группа.

+ -
HgC4H9OH

тока i (А/м2)
Поверхность (площадь электрода) S (м2) (скорость электродного процесса)

Напряжение U

(В) Потенциал электрода E (В)

Заряд q (Кл) Удельный заряд, или плотность заряда
q (Кл/м2)

Емкость С (Ф/м2)

Поверхностное (пограничное) натяжение  (Н/м)

Поверхностный избыток Г (моль/м2)

Адсорбционный метод
Электрокапиллярный метод
Вольтамперометрические и кулонометрические методы

образовании ДЭС. φ0=1В, Сconst=0,2 Ф/м2
1. Адсорбционный метод

постоянном составе раствора
Электрокапиллярный метод позволяет опре­делить заряд поверхности электрода, потенциал

нулевого заряда, поверхност­ные избытки катионов и анионов, а также нейтральных органи­ческих молекул — Горг. Путем двукратного дифференцирования электрокапиллярной кривой можно определить дифференциальную емкость двойного элек­трического слоя:

при специфической адсорбции

электрохимическая реакция. Все подводимое электричество расходуется на заряжение двойного слоя.
снижение

C при снижении концентрации раствора

Кривые емкости ДЭС висмутового электрода в 0,1 М водных растворах галогенидов калия

Зависимость емкости ДЭС ртутного электрода от приведенного потенциала 0

приемлемые значения емкости ДЭС, но не объясняет зависимость C, 

от концентрации электролита и температуры.

1. Г. Гельмгольц, 1853 г. (Модель плоского конденсатора)

Ионы – это точечные заряды.
Недостатки: аномально высокие значения емкости ДЭС,

не объясняет явления специфической адсорбции ионов.

внешней плоскостях Гельмгольца, их емкости складываются по принципу соединения двух

последовательно соединенных конденсаторов , 2) считал, что емкость ДЭС не зависит от заряда поверхности и концентрации электролита.

электролит (модель Грэма), отсутствие специфической адсорбции;
в – наличие специфической

адсорбции, знаки заряда электрода и иона совпадают;
г – наличие специфической адсорбции, знаки заряда электрода и иона различаются.

Распределение потенциала в ДЭС на границе раздела «электрод-электролит»

этому ионистор можно быстро зарядить и использовать, тогда, как на

заряд аккумуляторных батарей уходит значительное время;
Количество циклов заряд/разряд – более 100000;
Не требуют обслуживания;
Небольшой вес и габариты;
Для заряда не требуется сложных зарядных устройств;Работает в широком диапазоне температур (-40…+700C). При температуре больше +700С ионистор, как правило, разрушается;
Длительный срок службы.

Высокая стоимость;
Малое напряжение на одном элементе ионистора;
Удельная энергия симметричных ионисторов меньше, чем у аккумуляторов (5–12 Вт·ч/кг при 200 Вт·ч/кг для литий-ионных аккумуляторов);
Значительно больший, по сравнению с аккумуляторами, саморазряд: порядка 1 мкА у ионистора 2 Ф × 2,5 В.

состоит из нескольких стадий:
Собственно электродная реакция: Oxz+ + ne =

Redz-n
Массоперенос (доставка вещества в зону реакции и отвод продуктов в объем раствора или электрода)
Адсорбция реагентов и продуктов на поверхности электрода.
Перемещение реагентов по поверхности электрода
Предшествующая или последующая (относительно электродной реакции) химическая реакция в объеме раствора или на поверхности электрода
И некоторые другие возможные стадии.
При последовательном протекании реакций лимитирующей стадией является та, у которой наименьшая скорость. При параллельном протекании реакций – та, у которой скорость наибольшая.
В нашем курсе будем рассматривать закономерности протекания каждой отдельной из возможных стадий и их некоторое сочетание.

E(i)).


Часто для электродных процессов Ер неизвестно, тогда используют расчетное значение.

Система знаков:
Катодные процессы – перенос электрона из электрода в раствор. Считаем катодные токи положительными. При этом катодные перенапряжения отрицательными.
Анодные процессы - перенос электрона из раствора на электрод. Считаем анодные токи отрицательными. При этом анодные перенапряжения положительными.

+ Eа
Из U выделить поляризацию одного электрода трудно, особенно, если

электроды из разных материалов. Используют вспомогательный электрод. Также подбирают соотношение площадей электродов.

При наложении напряжения U (потенциала) на ячейку происходит поляризация катода (Eк) и анода (Eа), также имеет место падение напряжения в растворе.

+ nē  Redz-n
Частица Ox может быть нейтральной молекулой или

ионом. Изменение заряда происходит в одной элементарной стадии, а не путем последовательного переноса n электронов.
Скорость химической реакции 1-го порядка подчиняется ур-ю Аррениуса
V = kCexp(-GaRT)
где k- константа реакции, C- концентрация реагента, Ga- энергия активации.
В электродных реакциях появляется дополнительный параметр – потенциал электрода. Дальнейшее рассмотрение также основано на том, что энергия активации линейным образом зависит от потенциала электрода: Ga= nF
Обозначим скорость катодного процесса выраженную в электрических единицах (А/см2), через , а абсолютную скорость анодного процесса через .
При указанных допущениях для катодного процесса можно записать:

плотность тока обмена, важная кинетическая характеристика стадии переноса электрона, указывающая

на степень обратимости электрохимической реакции. Чем больше i0, тем более обратимой является данная реакция.

- константы скорости прямого и обратного процесса; α и  - коэффициенты, отражающие линейную зависимость энергии активации катодного и анодного процессов от от ∆φ (коэффициенты переноса).

выполняется условие  

в линейную зависимость тока от перенапряжения:

При больших перенапряжениях, где выполняется условие  >> RT/F 25мВ (практически >100 мВ) второй экспонентой в уравнении можно пренебречь: