Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Optimization of Nonlinear, Coupled Fluid-Thermal Systems
Содержание
- 1. Optimization of Nonlinear, Coupled Fluid-Thermal Systems
- 2. Presentation OutlineOverviewProject GoalsMicrogravity ResearchMGFLOOptimization TheoryPrevious Work Code Details Overview Validation Applications Conclusions Recommendations
- 3. Project Goals To Design and Implement an optimization algorithm for a fluid-thermal simulatorMGFLOBoundary Condition Manipulation
- 4. Microgravity Fluid ResearchSurface TensionSmallest Surface Area PossibleDominated
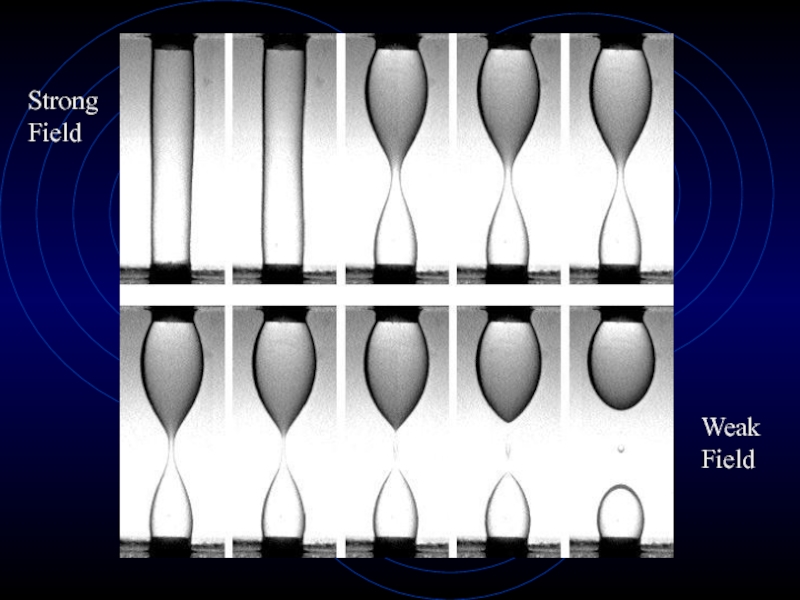
- 5. StrongFieldWeak Field
- 6. Microgravity Test FacilitiesDrop TowersEvacuated tubes used to
- 7. Test FacilitiesNASA’s KC-135 “Vomit Comet”Parabolic flight pattern
- 8. Test FacilitiesSounding RocketsAlso flown in a parabolic
- 9. Microgravity SimulationComputational Fluid Dynamics (CFD) allows cost-effective
- 10. Incompressible Navier-Stokes Equations:Energy Equation:Governing Equations
- 11. MGFLODeveloped Under NASA-Grand Challenge SupportParallel, Finite Element
- 12. Optimization TheoryAttempt to find “best value” of
- 13. Nelder and Mead’s MethodEfficient search method for
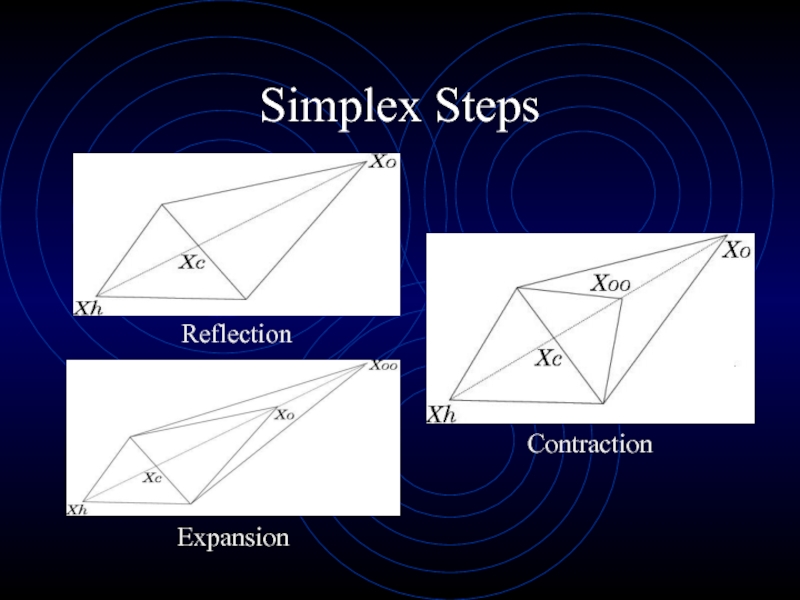
- 14. Simplex StepsReflectionExpansionContraction
- 15. Previous WorkInvestigated Operation of the MGFLO CodeDesigned
- 16. Code OverviewDeveloped Matlab Routines to Analyze MGFLO
- 17. Code FunctionsInitializes the solutionCalls MGFLO for each
- 18. Слайд 18
- 19. Debugging & ValidationAttempt to find answer to
- 20. Слайд 20
- 21. Слайд 21
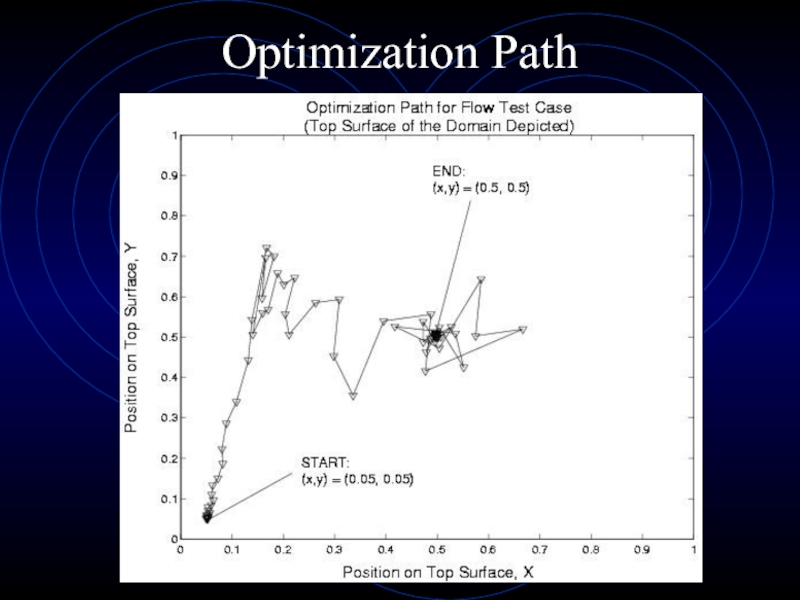
- 22. Optimization Path
- 23. LimitationsMerit function dependence for pathological problemsNot successful
- 24. ApplicationsSolve more complicated problem whose answer is
- 25. Слайд 25
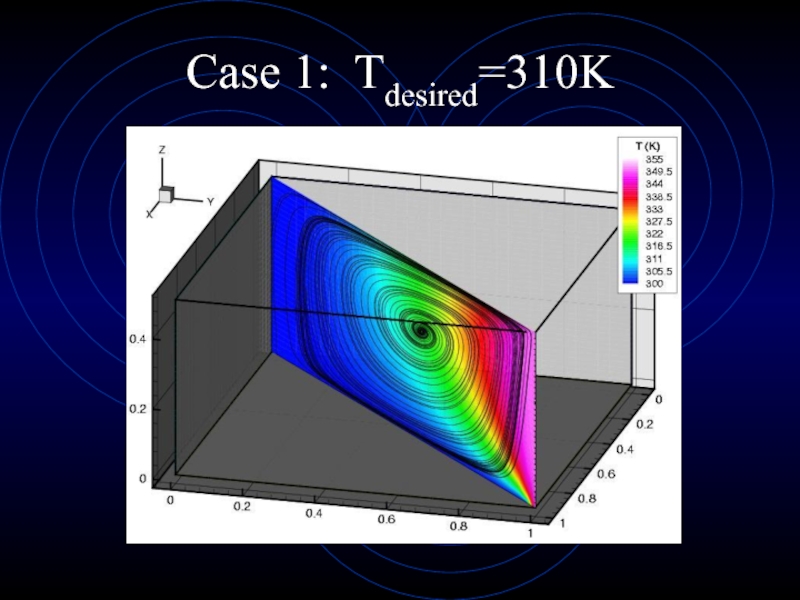
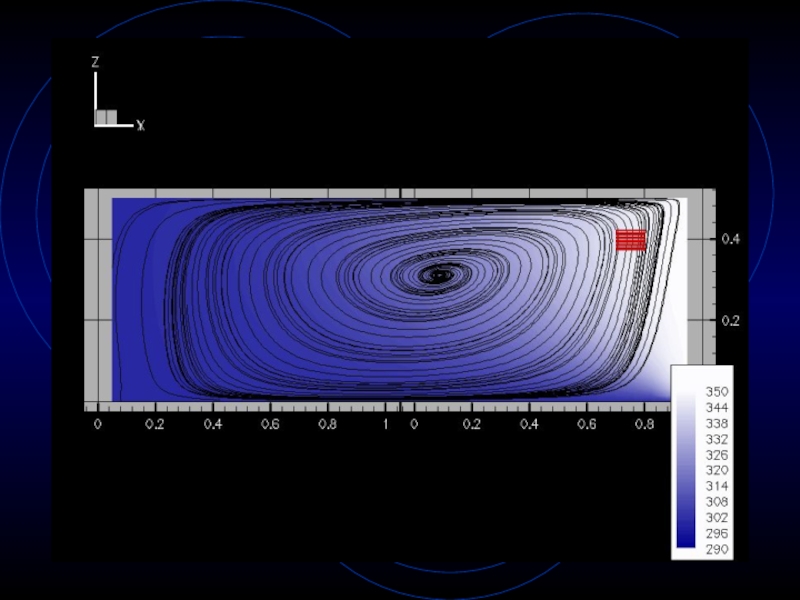
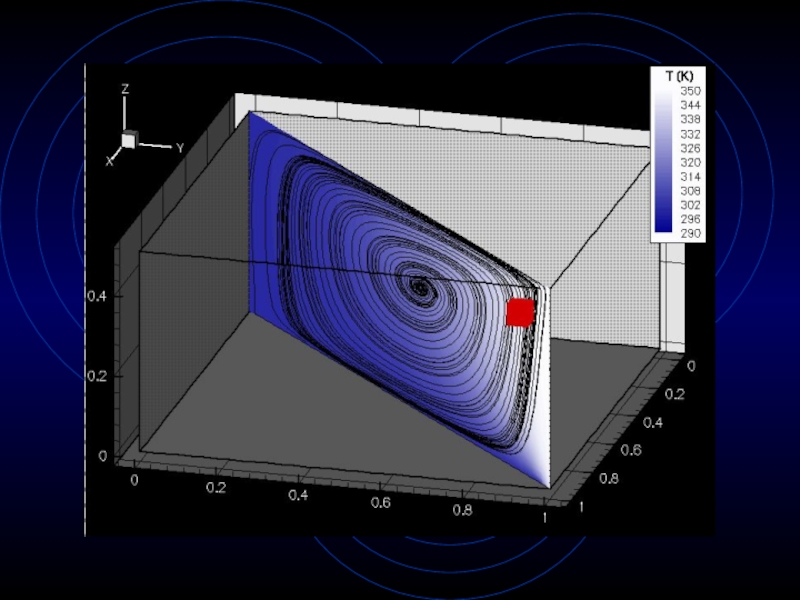
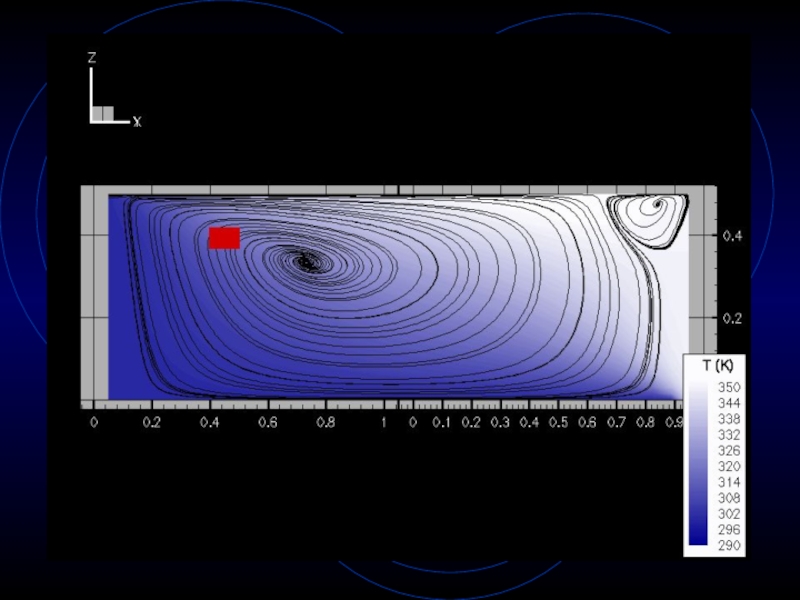
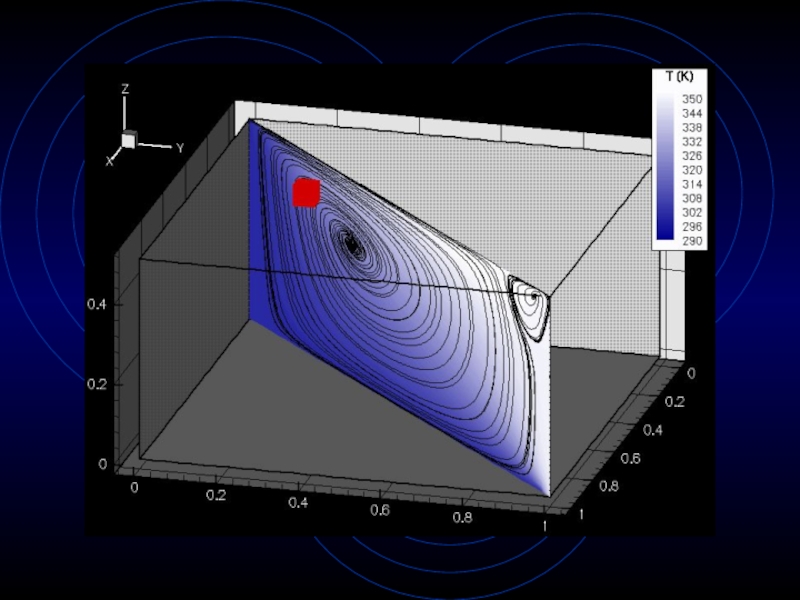
- 26. Case 1: Tdesired=310K
- 27. Particle Tracing AlgorithmHeun predictor-corrector methodSecond-order accurate in time Allows visualization/quantification of mixing
- 28. Слайд 28
- 29. Слайд 29
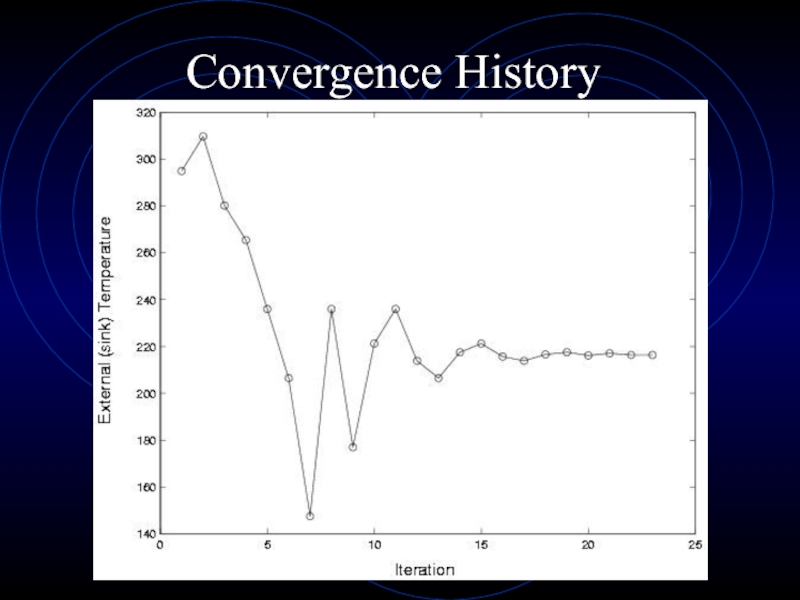
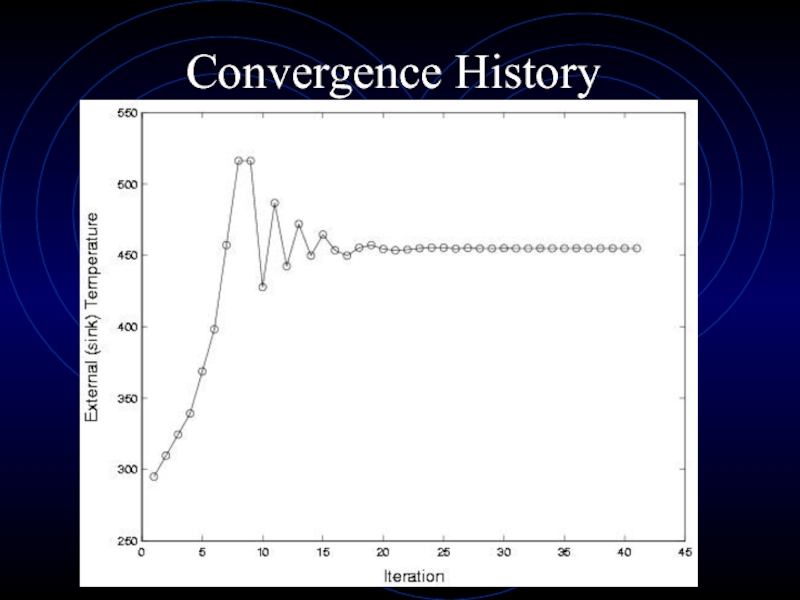
- 30. Convergence History
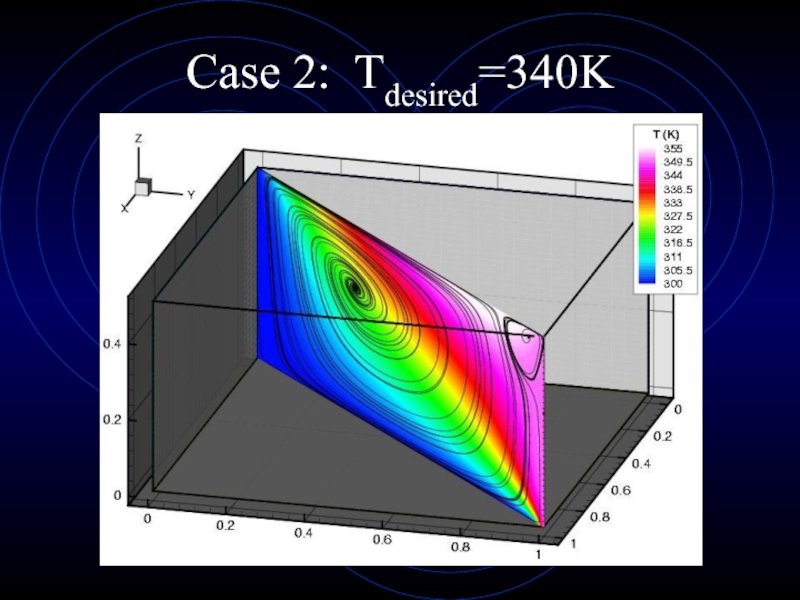
- 31. Case 2: Tdesired=340K
- 32. Слайд 32
- 33. Слайд 33
- 34. Convergence History
- 35. ConclusionsWe became familiar with the CFDLab and
- 36. RecommendationsUse particle tracing algorithm to optimize system
- 37. Questions?
- 38. Скачать презентанцию
Presentation OutlineOverviewProject GoalsMicrogravity ResearchMGFLOOptimization TheoryPrevious Work Code Details Overview Validation Applications Conclusions Recommendations
Слайды и текст этой презентации
Слайд 2Presentation Outline
Overview
Project Goals
Microgravity Research
MGFLO
Optimization Theory
Previous Work
Code Details
Overview
Validation
Applications
Conclusions
Recommendations
Слайд 3Project Goals
To Design and Implement an optimization algorithm for a
fluid-thermal simulator
MGFLO
Boundary Condition Manipulation
Слайд 4Microgravity Fluid Research
Surface Tension
Smallest Surface Area Possible
Dominated on Earth by
Gravity, which Makes Surfaces Flat
Liquid Bridges
ALEX: A Liquid Electrohydrodynamics eXperiment
Surface
Tension Dominates with Decreased Electric FieldIn a microgravity environment, surface tension and
thermocapillary effects can be dominant.
Слайд 6Microgravity Test Facilities
Drop Towers
Evacuated tubes used to expose experiments to
several seconds of microgravity
Only short durations of microgravity are achieved
Слайд 7Test Facilities
NASA’s KC-135 “Vomit Comet”
Parabolic flight pattern can produce up
to 30 seconds of microgravity
Several periods of microgravity in one
flightСлайд 8Test Facilities
Sounding Rockets
Also flown in a parabolic flight path to
produce microgravity
Can provide 6-7 minutes of microgravity
Слайд 9Microgravity Simulation
Computational Fluid Dynamics (CFD) allows cost-effective microgravity simulation
Advances in
parallel supercomputing allow large problems to be solved
Слайд 11MGFLO
Developed Under NASA-Grand Challenge Support
Parallel, Finite Element Formulation of Navier-Stokes
and Energy Equations
Allows for Coupled and Uncoupled Solution
Systems Optimized Through
Matlab Using Existing AlgorithmsСлайд 12Optimization Theory
Attempt to find “best value” of a merit function
within defined constraints
Gradient versus non-gradient methods
Gradient methods can be complex
and require several merit function evaluationsNon-gradient methods optimize based on a sample set of merit function values
Nelder-Mead Simplex Search Algorithm
Слайд 13Nelder and Mead’s Method
Efficient search method for minimizing a merit
function of up to six variables
Optimization points are nodes of
a polygon Optimal solution is determined by:
Reflection
Expansion
Contraction
Слайд 15Previous Work
Investigated Operation of the MGFLO Code
Designed Simple Optimization Routine
in Matlab
Established Algorithms to Optimize Complex Fluid-Thermal Systems
Слайд 16Code Overview
Developed Matlab Routines to Analyze MGFLO Output.
Matlab Can Compute
Quantities of Interest:
Vorticity, Divergence
Gradient, Laplacian
0th, 1st, 2nd Order
Derivatives Normal to Walls Average Quantities in Large Datasets
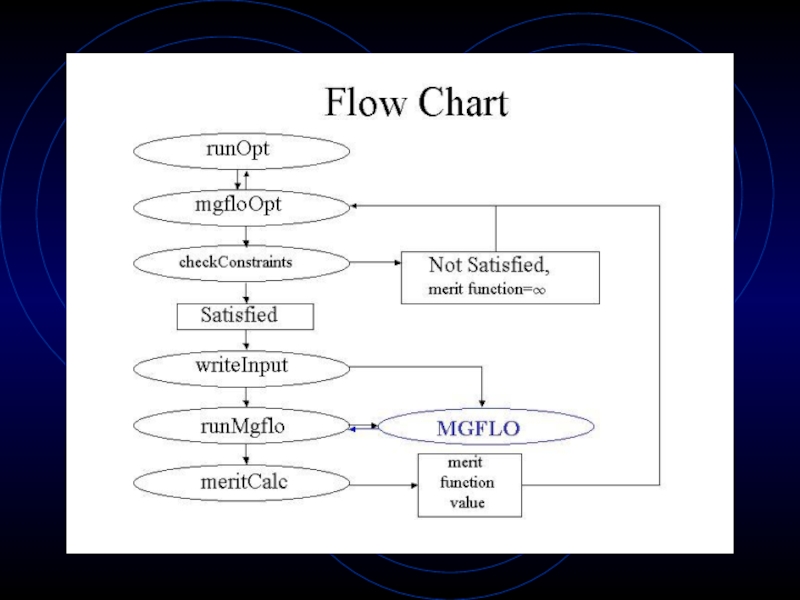
Слайд 17Code Functions
Initializes the solution
Calls MGFLO for each simplex step
Checks that
user-specified constraints are satisfied
Calculates the user-specified merit function
Allows user to
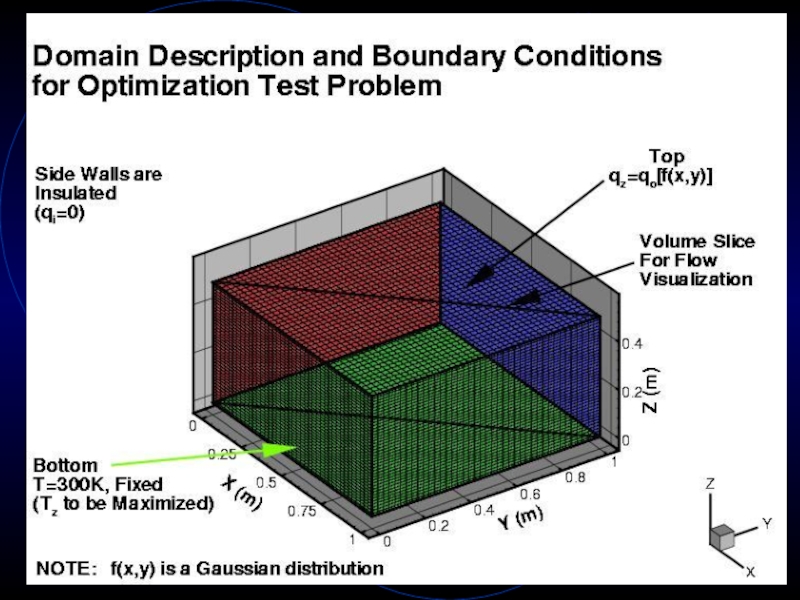
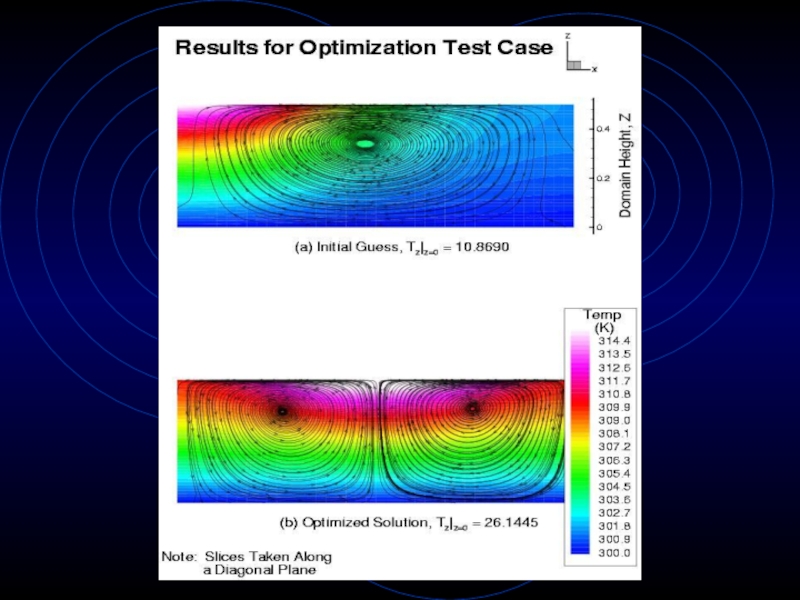
monitor solution progressionСлайд 19Debugging & Validation
Attempt to find answer to a known problem
Position
heat source on top surface to maximize heat flux out
of the bottomRun on the 16-node Beowulf cluster in the CFDLab
Слайд 23Limitations
Merit function dependence for pathological problems
Not successful at maximizing vorticity
in previous case
Non-smooth merit functions (too many local maxima)
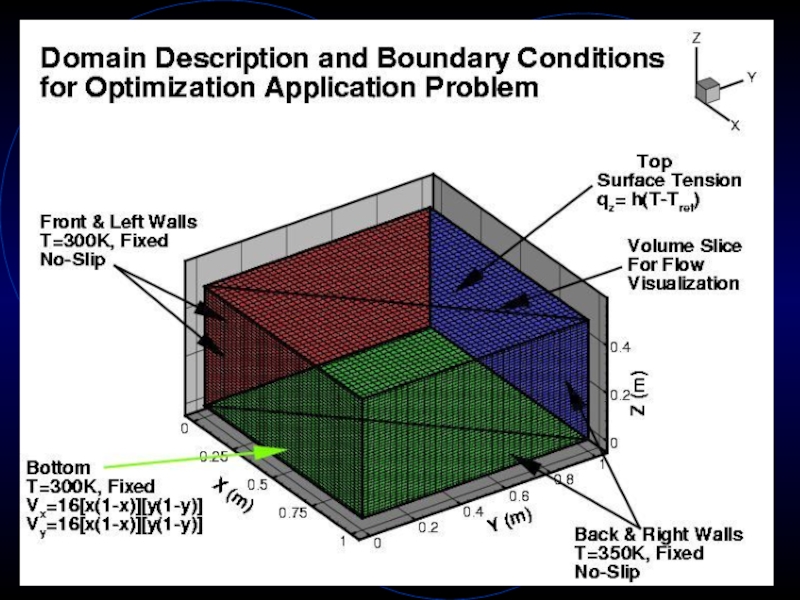
Слайд 24Applications
Solve more complicated problem whose answer is not known a-priori
System
exposed to external environment via Newton’s law of cooling (mixed
boundary condition)Use particle tracing as a visualization technique
Слайд 27Particle Tracing Algorithm
Heun predictor-corrector method
Second-order accurate in time
Allows visualization/quantification
of mixing
Слайд 35Conclusions
We became familiar with the CFDLab and the MGFLO code
Successfully
developed a method to optimize nonlinear fluid-thermal systems
Implemented a particle
tracing algorithm in Matlab to visualize fluid mixingСлайд 36Recommendations
Use particle tracing algorithm to optimize system mixing (currently takes
a long time!)
Implement feedback control for time-varying systems
Calculate merit function
interior to MGFLO Faster
More accurate
Support unstructured grids