TheSlide.ru

13. ДИСПЕРСИЯ И ЕЕ СВОЙСТВА Дисперсия - это мера рассеяния значений случайной

Содержание

1. 13. ДИСПЕРСИЯ И ЕЕ СВОЙСТВА Дисперсия - это мера рассеяния значений случайной
2. Найдем математическое ожидание и дисперсию этой случайной величины. Например, пусть случайная величина Х задана рядом распределения:
3. Для вычисления дисперсии часто используют другую формулу:
4. Доказательство:Используем свойства математического ожидания:
5. СВОЙСТВА ДИСПЕРСИИДисперсия от постоянной величины равна нулю: D[C]=0, C=const1
6. Доказательство:Используем второе выражение для дисперсии. Так как M[C]=C, M[C2]=C2тоD[C]=M[C2]-(M[C])2=C2-C2=0
7. Дисперсия суммы случайной величины Х и постоянной величины С равна дисперсии величины Х : D[X+С]=D[X]2
8. Доказательство:По свойству математического ожидания:М[X+С]=M[X]+СПоэтому на основании определения дисперсии:
9. Постоянная величина выносится за знак дисперсии в квадрате: D[k X]=k2 D[X]3
10. Доказательство:По свойству математического ожидания:Используем определение дисперсии:
11. 4Дисперсия всегда неотрицательна:
12. 5Дисперсия суммы двух случайных величин находится по формуле:
13. Величина KXY называется корреляционным моментом случайных величин X и Y:
14. Математическое ожидание суммы равно сумме математических ожиданий:Распишем дисперсию суммы случайных величин по определению дисперсии:Доказательство:
15. Перегруппируем слагаемые:Снова используем свойства математического ожидания:Под знаком математического ожидания раскрываем квадрат суммы:
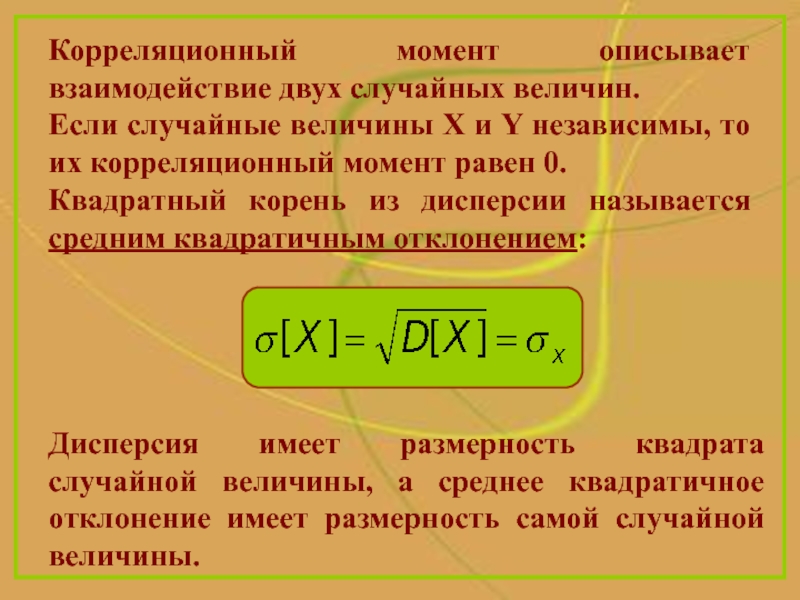
16. Корреляционный момент описывает взаимодействие двух случайных величин.
17. Скачать презентанцию

Найдем математическое ожидание и дисперсию этой случайной величины. Например, пусть случайная величина Х задана рядом распределения:

Главная
Разное
13. ДИСПЕРСИЯ И ЕЕ СВОЙСТВА Дисперсия - это мера рассеяния значений случайной

Слайды и текст этой презентации

Слайд 113. ДИСПЕРСИЯ И ЕЕ СВОЙСТВА
Дисперсия - это мера рассеяния
значений

случайной величины
около ее математического
ожидания:

13. ДИСПЕРСИЯ И ЕЕ СВОЙСТВАДисперсия - это мера рассеяния значений случайной величины около ее математического ожидания:

Слайд 2Найдем математическое ожидание и дисперсию этой случайной величины.
Например, пусть

случайная величина Х задана рядом распределения:

Найдем математическое ожидание и дисперсию этой случайной величины. Например, пусть случайная величина Х задана рядом распределения:

Слайд 3Для вычисления дисперсии часто используют другую формулу:

Для вычисления дисперсии часто используют другую формулу:

Слайд 4Доказательство:
Используем свойства математического ожидания:

Доказательство:Используем свойства математического ожидания:

Слайд 5СВОЙСТВА ДИСПЕРСИИ
Дисперсия от постоянной
величины
равна нулю: D[C]=0, C=const
1

СВОЙСТВА ДИСПЕРСИИДисперсия от постоянной величины равна нулю: D[C]=0, C=const1

Слайд 6Доказательство:
Используем второе выражение для дисперсии. Так как
M[C]=C, M[C2]=C2
то
D[C]=M[C2]-(M[C])2=C2-C2=0

Доказательство:Используем второе выражение для дисперсии. Так как M[C]=C, M[C2]=C2тоD[C]=M[C2]-(M[C])2=C2-C2=0

Слайд 7Дисперсия суммы случайной
величины Х и постоянной
величины С равна

дисперсии
величины Х : D[X+С]=D[X]
2

Дисперсия суммы случайной величины Х и постоянной величины С равна дисперсии величины Х : D[X+С]=D[X]2

Слайд 8Доказательство:
По свойству математического ожидания:
М[X+С]=M[X]+С
Поэтому на основании определения дисперсии:

Доказательство:По свойству математического ожидания:М[X+С]=M[X]+СПоэтому на основании определения дисперсии:

Слайд 9Постоянная величина
выносится за знак дисперсии
в квадрате: D[k X]=k2

D[X]
3

Постоянная величина выносится за знак дисперсии в квадрате: D[k X]=k2 D[X]3

Слайд 10Доказательство:
По свойству математического ожидания:
Используем определение дисперсии:

Доказательство:По свойству математического ожидания:Используем определение дисперсии:

Слайд 114
Дисперсия всегда неотрицательна:

4Дисперсия всегда неотрицательна:

Слайд 125
Дисперсия суммы двух случайных
величин находится по формуле:

5Дисперсия суммы двух случайных величин находится по формуле:

Слайд 13Величина KXY называется
корреляционным моментом
случайных величин X и Y:

Величина KXY называется корреляционным моментом случайных величин X и Y:

Слайд 14Математическое ожидание суммы равно сумме математических ожиданий:
Распишем дисперсию суммы случайных

величин по определению дисперсии:
Доказательство:

Математическое ожидание суммы равно сумме математических ожиданий:Распишем дисперсию суммы случайных величин по определению дисперсии:Доказательство:

Слайд 15Перегруппируем слагаемые:
Снова используем свойства математического ожидания:
Под знаком математического ожидания раскрываем

квадрат суммы:

Перегруппируем слагаемые:Снова используем свойства математического ожидания:Под знаком математического ожидания раскрываем квадрат суммы:

Слайд 16Корреляционный момент описывает взаимодействие двух случайных величин.
Если случайные величины

X и Y независимы, то их корреляционный момент равен 0.
Квадратный

корень из дисперсии называется средним квадратичным отклонением:

Дисперсия имеет размерность квадрата случайной величины, а среднее квадратичное отклонение имеет размерность самой случайной величины.

Корреляционный момент описывает взаимодействие двух случайных величин. Если случайные величины X и Y независимы, то их корреляционный

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей