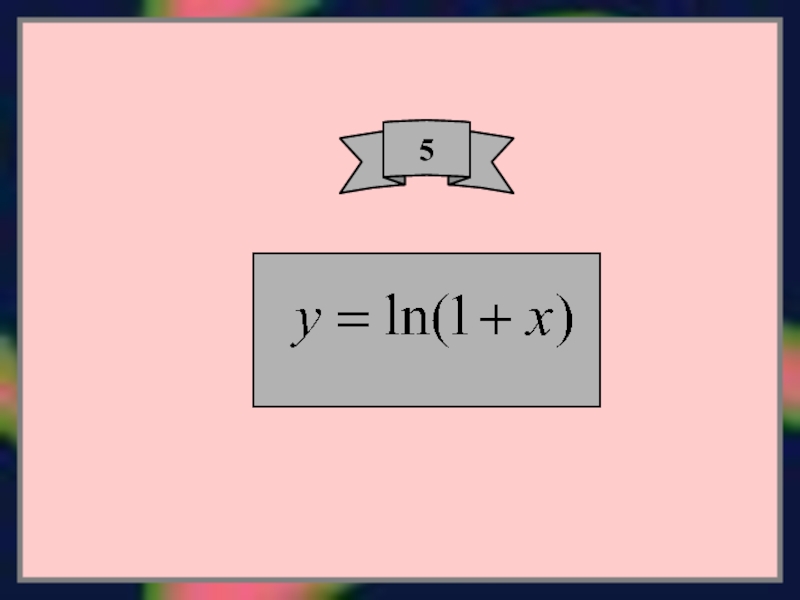Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
14.4. РАЗЛОЖЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В РЯД МАКЛОРЕНА 1
Содержание
- 1. 14.4. РАЗЛОЖЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В РЯД МАКЛОРЕНА 1
- 2. Подставляем найденные величины в ряд Маклорена:
- 3. Область сходимости ряда
- 4. 2
- 5. Слайд 5
- 6. Производные четного порядка все равны нулю:Производные нечетного порядка равны:гдеПодставляем найденные величины в ряд Маклорена:
- 7. Область сходимости ряда
- 8. 3
- 9. Слайд 9
- 10. Производные нечетного порядка все равны нулю:Производные четного порядка равны:гдеПодставляем найденные величины в ряд Маклорена:
- 11. Область сходимости ряда
- 12. 4
- 13. Следовательно:
- 14. Подставляем найденные величины в ряд Маклорена:
- 15. Интервал сходимости ряда
- 16. Этот ряд называется биномиальным.Если число m –
- 17. 5
- 18. Слайд 18
- 19. Область сходимости ряда
- 20. ПРИМЕР.Разложить в ряд функцию
- 21. РЕШЕНИЕ.
- 22. Скачать презентанцию
Подставляем найденные величины в ряд Маклорена:
Слайды и текст этой презентации
Слайд 6Производные четного порядка все равны нулю:
Производные нечетного порядка равны:
где
Подставляем найденные
величины в ряд Маклорена:
Слайд 10Производные нечетного порядка все равны нулю:
Производные четного порядка равны:
где
Подставляем найденные
величины в ряд Маклорена:
Слайд 16Этот ряд называется биномиальным.
Если число m – целое и положительное,
то биномиальный ряд представляет собой формулу бинома Ньютона, т.к. при
n=m+1
m-n+1=0
следовательно n-ый и все последующие члены ряда будут равны нулю, т.е. ряд обрывается и вместо бесконечного разложения получается конечная сумма.