lection4.ppt

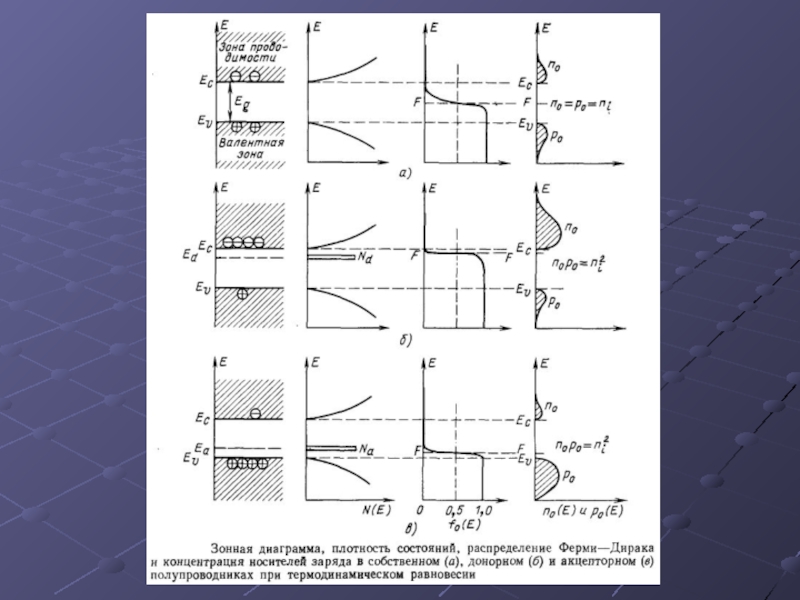
акцепторной примесей, nd, pa – концентрации электронов и дырок в

Концентрация положительно и отрицательно заряженных ионов в донорном и акцепторном п/п, соответственно, вычисляется:
pd=Nd-nd и na=Na-pa .

ДОНОРНЫЙ ПОЛУПРОВОДНИК:

АКЦЕПТОРНЫЙ ПОЛУПРОВОДНИК:

Интеграл Ферми-Дирака с индексом ½.
- Эффективная плотность состояний в зоне

зоны.
С учетом безразмерных величин:
- Интеграл Ферми-Дирака для валентной зоны.
- Эффективная

Донорный полупроводник. Введем обозначение:

Концентрация электронов на уровне донорной примеси:

Количество положительных ионов:

Акцепторный полупроводник. Введем обозначение:

Концентрация дырок на уровне акцепторной примеси:

Количество отрицательных ионов:

электронов и дырок:
2. Сильно вырожденный полупроводник:
3. Переход от невырожденного к

в зоне проводимости с энергией E=>Ec некоторыми компонентами в функции

Интеграл Ферми-Дирака запишется в виде:

Равновесные концентрации электронов и дырок:

концентрации свободных электронов и дырок равны:
Собственная концентрация:
Тогда:
Отсюда следует:

атомах и ионах примеси;
Рассеяние на вакансиях, дислокациях и т.д.
Количество рассеянных

Эффективное сечение рассеяния:

Вероятность столкновения (рассеяния):

Время и длину свободного пробега можно выразить через эффективное сечение:

Вероятность рассеяния на единичном интервале пути

Полная вероятность рассеяния:

Полная длина свободного пробега:

которая в общем случае зависит от энергии частиц:
Во внешнем электрическом

В равновесии:

соударений электронов с дефектами решетки:
Если отклонение распределения носителей заряда

Тогда :

косинусами:
Время релаксации при рассеянии на ионах:
Длина свободного пробега:

нейтральных атомах примеси:
Время релаксации при рассеянии на дислокациях кристаллической решетки: