Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция_3_Статистическое_изучение_взаимосвязи.ppt
Содержание
- 1. Лекция_3_Статистическое_изучение_взаимосвязи.ppt
- 2. 2Корреляционный и регрессионный анализОсновная задача статистики –
- 3. 3Корреляционный и регрессионный анализПредмет корреляционно-регрессионного анализа составляет исследова-ние статистических зависимостей между явлениями.Корреляционный анализРегрессионный анализ
- 4. 4Корреляционный анализ Диаграмма рассеянияПростейшим приемом при исследовании
- 5. 5Корреляционный анализ Линейный коэффициент корреляции ПирсонаНаиболее часто
- 6. Корреляционный анализ Линейный коэффициент корреляции ПирсонаОсновные свойства коэффициента корреляции:Нет линейной связи
- 7. 7Корреляционный анализ Линейный коэффициент корреляции ПирсонаПример 2.
- 8. 8Корреляционный анализ Линейный коэффициент корреляции ПирсонаПример 3.
- 9. 9Корреляционный анализ Линейный коэффициент корреляции ПирсонаПример 4.
- 10. 10Корреляционный анализ Проверка значимости коэффициента корреляцииЛинейный коэффициент корреляции для генеральной совокупности:
- 11. 11Корреляционный анализ Проверка значимости коэффициента корреляцииОценка значимости
- 12. 12Корреляционный анализ Проверка значимости коэффициента корреляцииПример 5. Исследовать значимость коэффициента корреляции, рассчитан-ного в примере 2.
- 13. 13Корреляционный анализ Проверка значимости коэффициента корреляцииВывод: прямая
- 14. 14Регрессионный анализДиаграмма рассеянияНаиболее распространенным способом построения уравнения
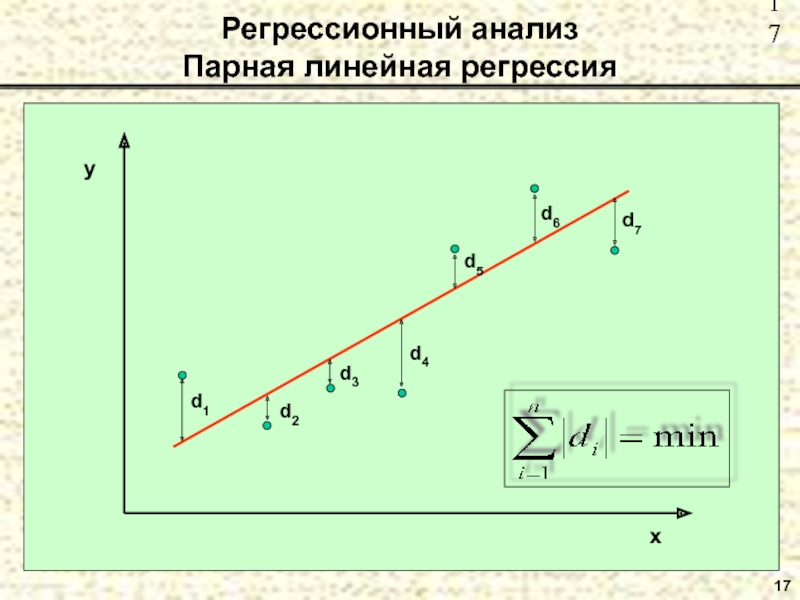
- 15. Регрессионный анализ Парная линейная регрессия
- 16. 16Регрессионный анализ Парная линейная регрессия
- 17. 17Регрессионный анализ Парная линейная регрессия
- 18. 18Пример 6. Построить уравнение линейной регрессии для
- 19. 19Пример 7. Построить уравнение линейной регрессии для
- 20. 20Пример 8. Построить уравнение линейной регрессии для данных, при-веденных в примере 4.Регрессионный анализ Парная линейная регрессия
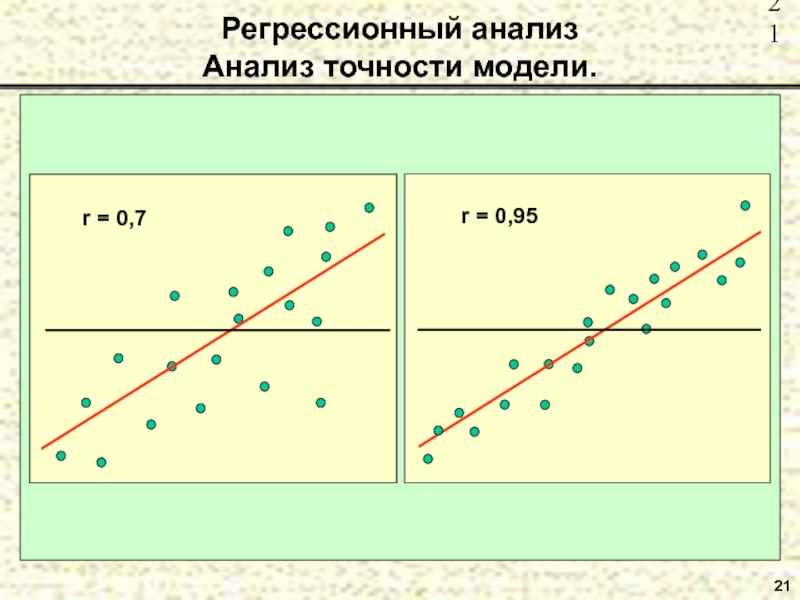
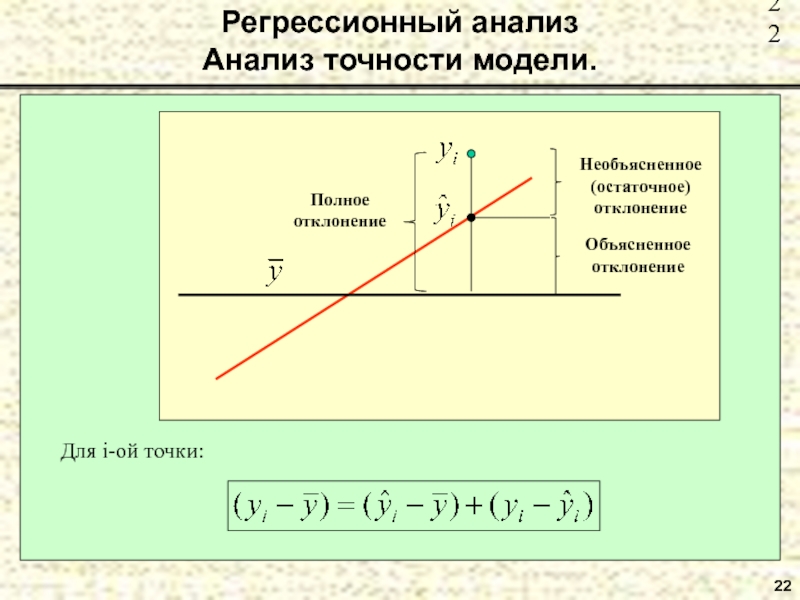
- 21. 21Регрессионный анализ Анализ точности модели.
- 22. 22Регрессионный анализ Анализ точности модели.Для i-ой точки:
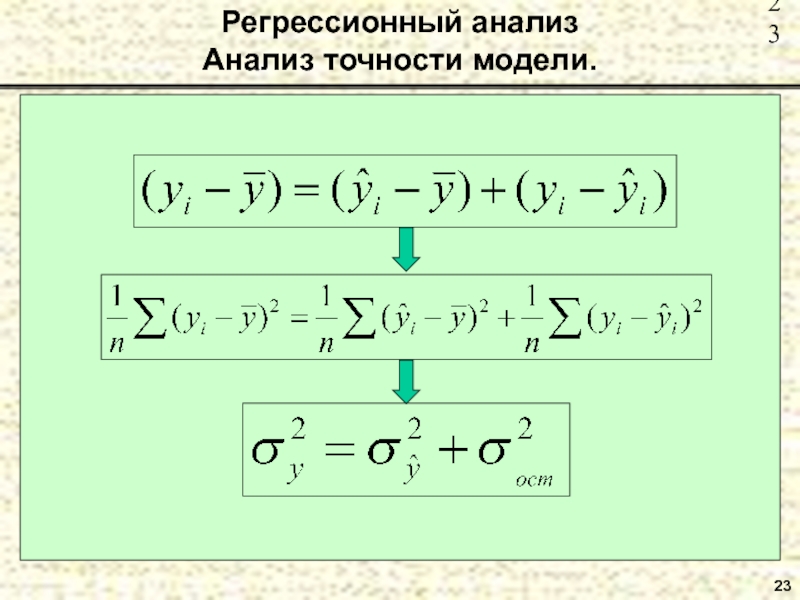
- 23. 23Регрессионный анализ Анализ точности модели.
- 24. 24Регрессионный анализ Анализ точности модели.Коэффициент детерминации:Коэффициент детерминации
- 25. 25Регрессионный анализ Стандартные ошибки.Помимо коэффициента детерминации, качество
- 26. 26Регрессионный анализ Схема проверки гипотез о значимости
- 27. 2727Регрессионный анализ Схема проверки гипотез о значимости
- 28. 2828Регрессионный анализ Проверка гипотезы о значимости модели.Для
- 29. 2929Регрессионный анализ Проверка гипотезы о значимости модели.Способы
- 30. 30Регрессионный анализ Проверка гипотезы о значимости модели2) С помощью стандартной функции Excel FРАСПОБР.FРАСПОБР(p;k1;k2)
- 31. 31Регрессионный анализ Нелинейная парная регрессияПример 10. В
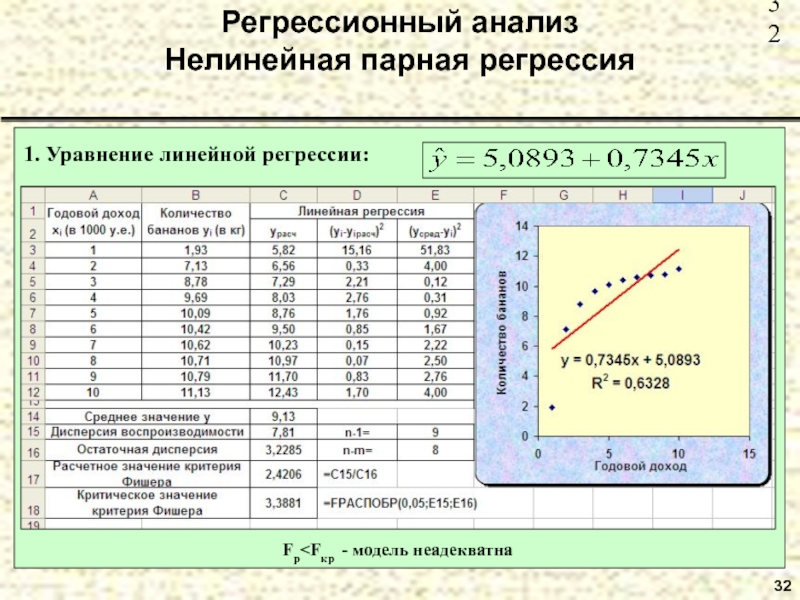
- 32. 32Регрессионный анализ Нелинейная парная регрессия1. Уравнение линейной регрессии:Fp
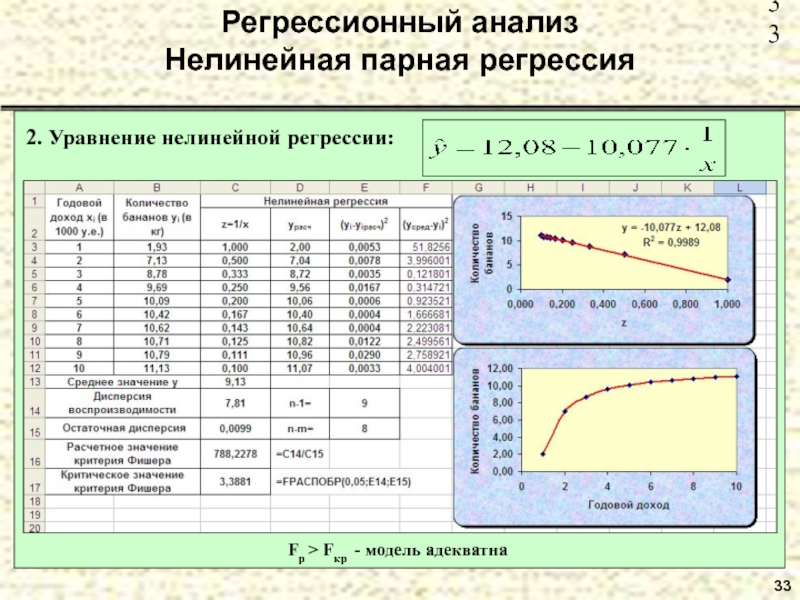
- 33. 33Регрессионный анализ Нелинейная парная регрессия2. Уравнение нелинейной регрессии:Fp > Fкр - модель адекватна
- 34. 34Регрессионный анализ Нелинейная парная регрессияНелинейные модели парной регрессии и преобразование переменных.a1
- 35. Скачать презентанцию
2Корреляционный и регрессионный анализОсновная задача статистики – обнаружить связь между явлениями, её вид и дать количественную характеристику этой связи.Вид связи между явлениями
Слайды и текст этой презентации
Слайд 1Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
СТАТИСТИКА
Лекция 3. Статистическое изучение взаимосвязи социально-экономических явлений.
Слайд 22
Корреляционный и регрессионный анализ
Основная задача статистики – обнаружить связь между
явлениями, её вид и дать количественную характеристику этой связи.
Вид связи
между явлениями
Слайд 33
Корреляционный и регрессионный анализ
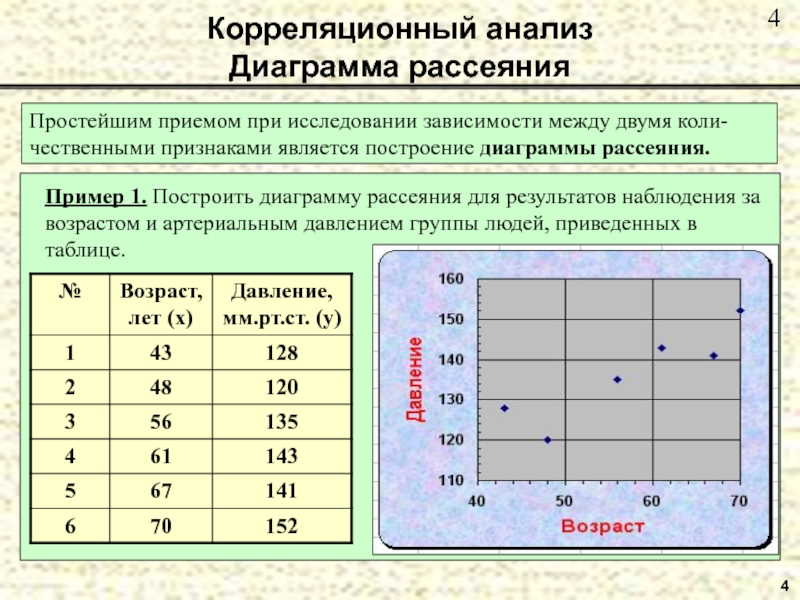
Предмет корреляционно-регрессионного анализа составляет исследова-ние статистических зависимостей
между явлениями.
Корреляционный анализ
Регрессионный анализ
Слайд 44
Корреляционный анализ
Диаграмма рассеяния
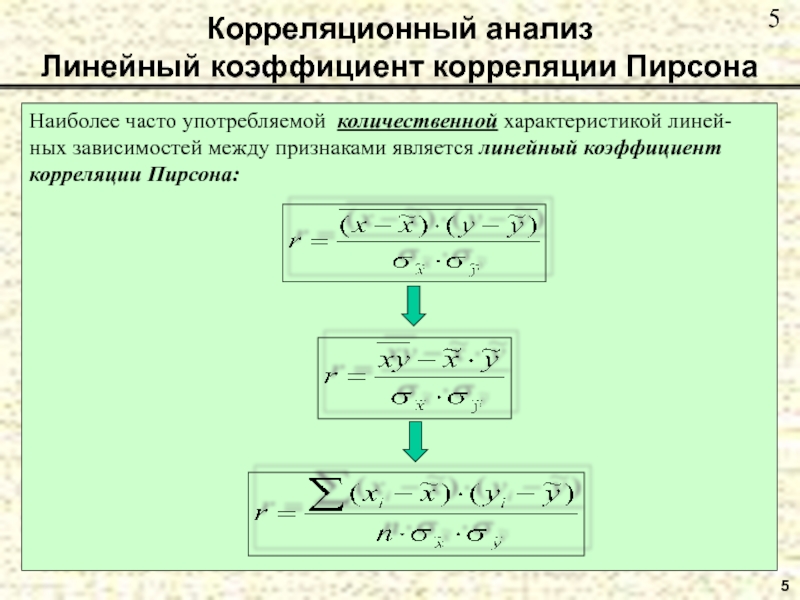
Простейшим приемом при исследовании зависимости между двумя коли-чественными
признаками является построение диаграммы рассеяния.
Пример 1. Построить диаграмму рассеяния для
результатов наблюдения за возрастом и артериальным давлением группы людей, приведенных в таблице.
Слайд 55
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
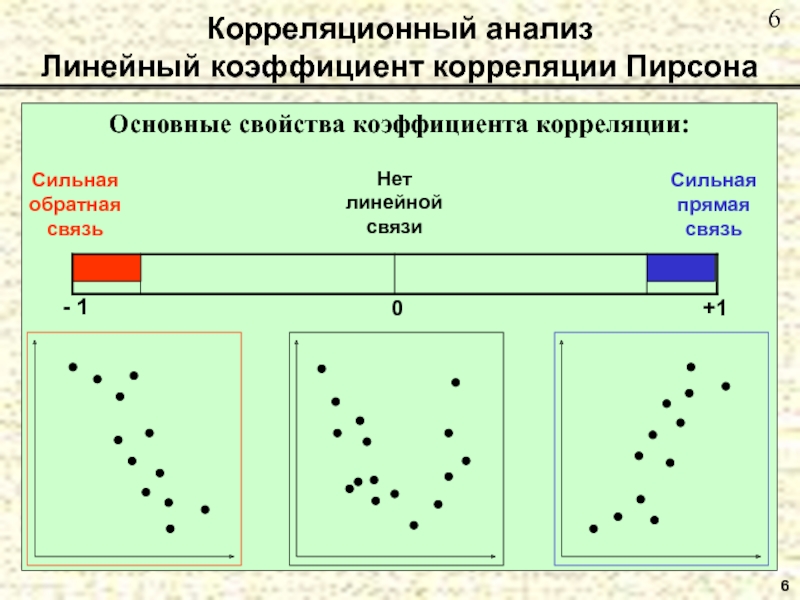
Наиболее часто употребляемой количественной характеристикой линей-ных
зависимостей между признаками является линейный коэффициент корреляции Пирсона:
Слайд 6Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Основные свойства коэффициента корреляции:
Нет линейной связи
Слайд 77
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
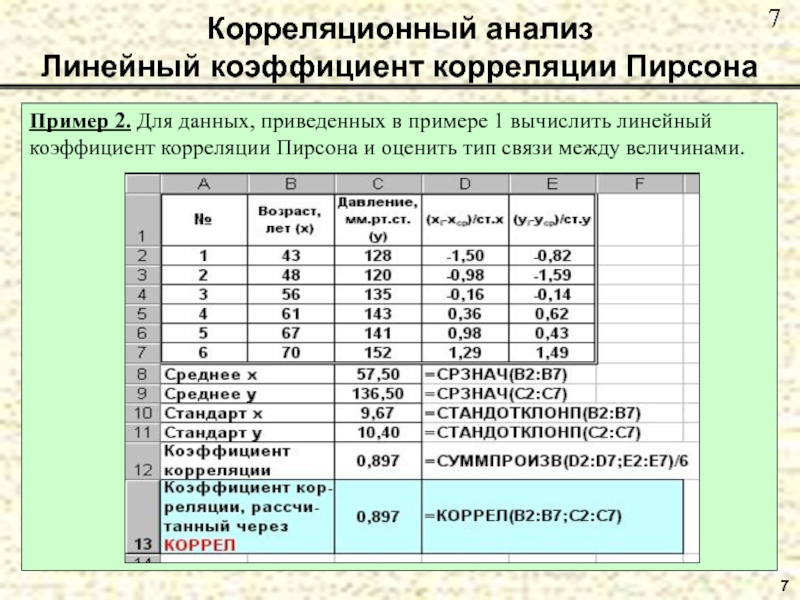
Пример 2. Для данных, приведенных в
примере 1 вычислить линейный коэффициент корреляции Пирсона и оценить тип
связи между величинами.
Слайд 88
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Пример 3. Для данных, приведенных в
таблице построить диаграмму рассеяния и вычислить коэффициент корреляции для группы
студентов (7 человек).
Слайд 99
Корреляционный анализ
Линейный коэффициент корреляции Пирсона
Пример 4. В таблице приведены данные
для группы курящих людей. По-строить диаграмму рассеяния и вычислить коэффициент
корреляции.
Слайд 1010
Корреляционный анализ
Проверка значимости коэффициента корреляции
Линейный коэффициент корреляции для генеральной совокупности:
Слайд 1111
Корреляционный анализ
Проверка значимости коэффициента корреляции
Оценка значимости коэффициента корреляции проводится с
помощью аппа-рата проверки гипотез.
Относительно генерального коэффициента корреляции можно выдвинуть две
гипотезы:генеральный коэффициент корреляции равен 0 (основная гипотеза);
генеральный коэффициент корреляции отличен от 0.
Сформировав выборку и рассчитав её коэффициент корреляции r, необходимо решить – является ли его значение настолько большим, чтобы вероятность (по различным выборкам) выпадения такого зна-чения при нулевом генеральном коэффициенте корреляции ρ была бы мала (меньше уровня значимости). Если является, то в этом слу-чае основная гипотеза отвергается, а коэффициент корреляции и ус-тановленная зависимость между величинами полагаются значимы-ми.
Слайд 1212
Корреляционный анализ
Проверка значимости коэффициента корреляции
Пример 5. Исследовать значимость коэффициента корреляции,
рассчитан-ного в примере 2.
Слайд 1313
Корреляционный анализ
Проверка значимости коэффициента корреляции
Вывод: прямая зависимость между возрастом человека
и артериальным давлением является значимой и её можно распространить на
всю сово-купность пациентов.
Слайд 1414
Регрессионный анализ
Диаграмма рассеяния
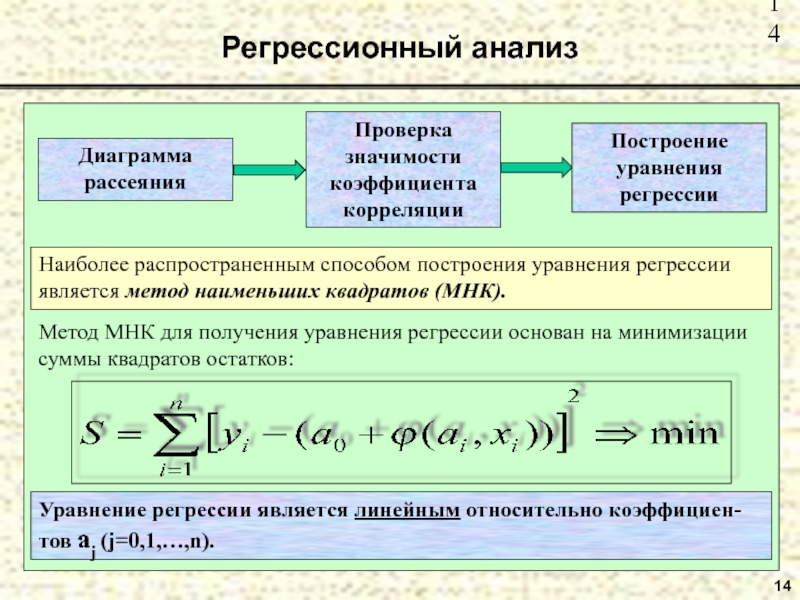
Наиболее распространенным способом построения уравнения регрессии является метод
наименьших квадратов (МНК).
Метод МНК для получения уравнения регрессии основан на
минимизации суммы квадратов остатков: Уравнение регрессии является линейным относительно коэффициен-тов aj (j=0,1,…,n).
Слайд 1818
Пример 6. Построить уравнение линейной регрессии для зависимости величин возраста
и давления, приведенных в примере 1.
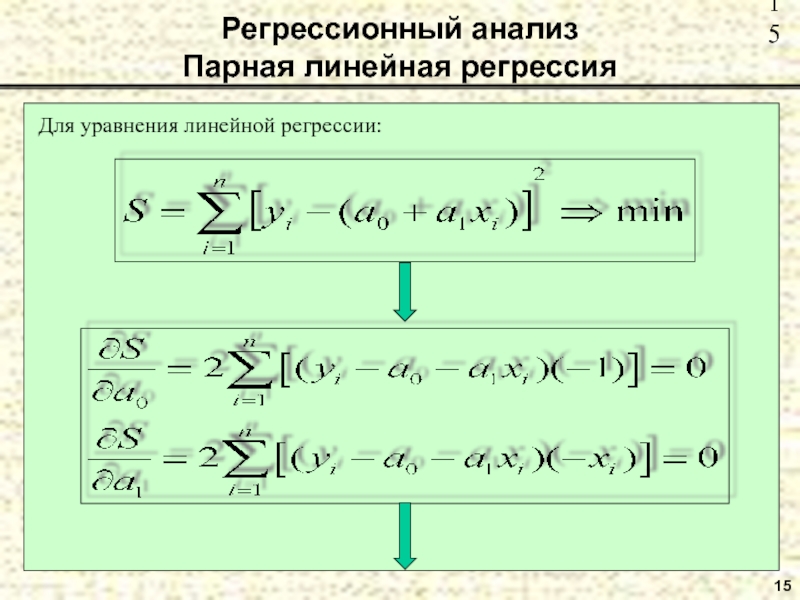
Регрессионный анализ
Парная линейная регрессия
Слайд 1919
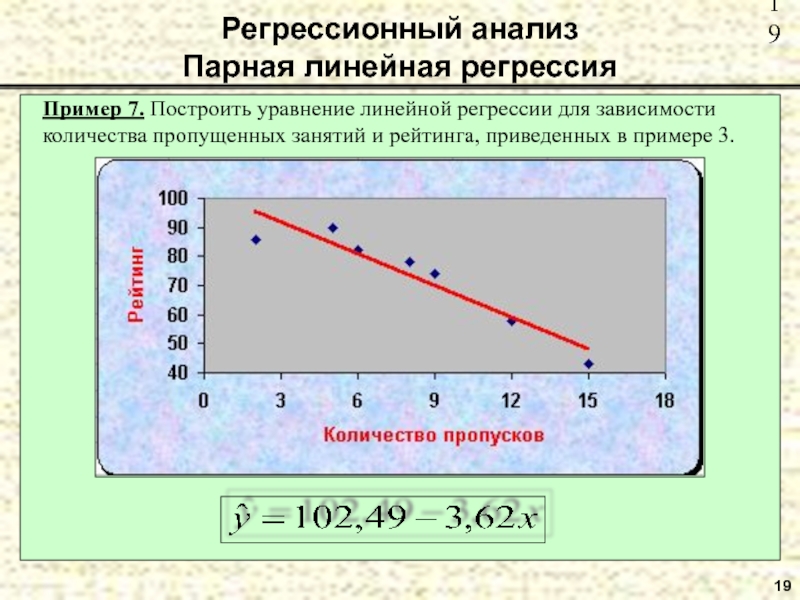
Пример 7. Построить уравнение линейной регрессии для зависимости количества пропущенных
занятий и рейтинга, приведенных в примере 3.
Регрессионный анализ
Парная линейная регрессия
Слайд 2020
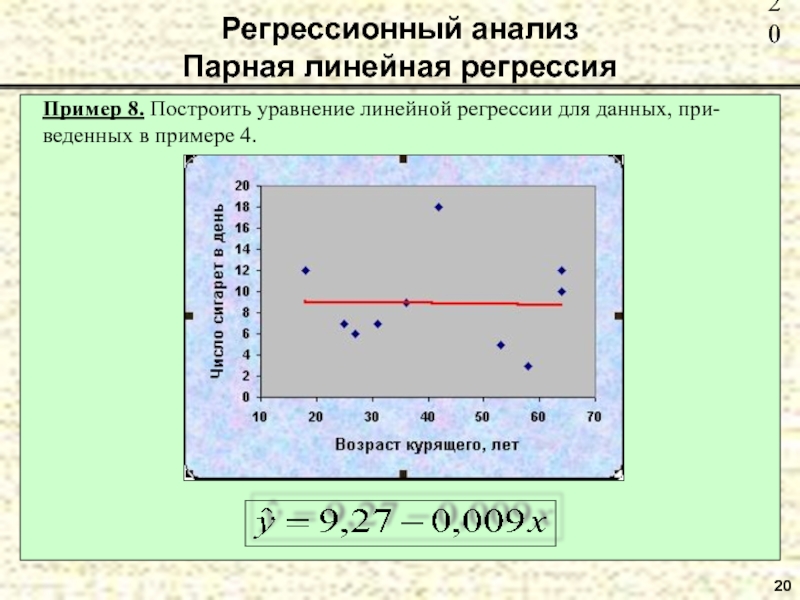
Пример 8. Построить уравнение линейной регрессии для данных, при-веденных в
примере 4.
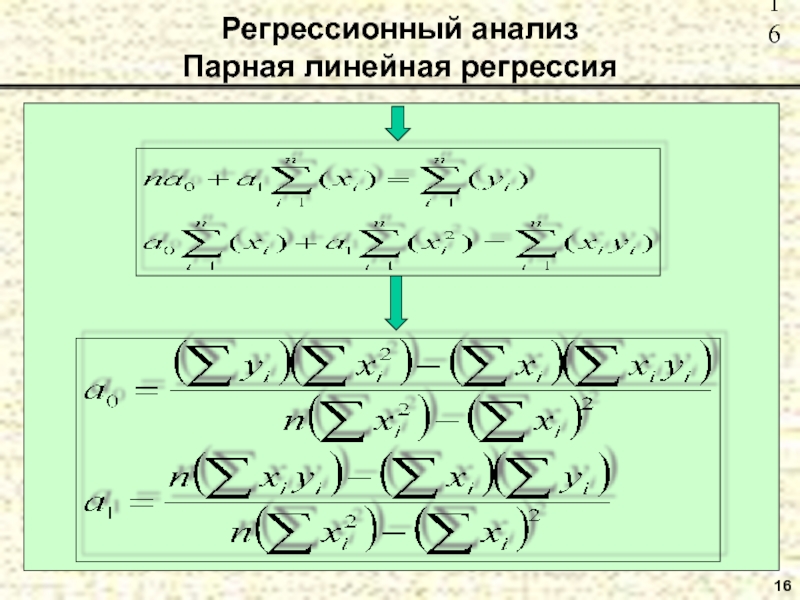
Регрессионный анализ
Парная линейная регрессия
Слайд 2424
Регрессионный анализ
Анализ точности модели.
Коэффициент детерминации:
Коэффициент детерминации является основной характеристикой регрессионной
модели и показывает, какую долю вариации (измен-чивости) результативного признака можно
объяснить изменением факторного признака.Одним из практических применений коэффициента детерминации является оценка качества и сравнение между собой различных мо-делей (линейной и нелинейных) парной регрессии.
Слайд 2525
Регрессионный анализ
Стандартные ошибки.
Помимо коэффициента детерминации, качество регрессионной моде-ли характеризуют стандартные
ошибки коэффициентов:
и стандартная ошибка модели:
где:
дисперсия независимой величины х
Слайд 2626
Регрессионный анализ
Схема проверки гипотез о значимости коэффициентов.
При уровне значимости
5% проверить гипотезы о значимости коэффициентов.
Пример 9. На основании данных
наблюдений в США за 25 – летний период (1959 – 1983 годы) построена зависимость суммарных расходов на питание (y) от располагаемых доходов (х):
Слайд 2727
27
Регрессионный анализ
Схема проверки гипотез о значимости коэффициентов.
1) Гипотезы для обоих
коэффициентов формулируются одинаково:
Н0: a0=0; H1: a0≠0.
Н0: a1=0; H1: a1≠0.
Слайд 2828
28
Регрессионный анализ
Проверка гипотезы о значимости модели.
Для решения вопроса действительно ли
полученное при оценке регрес-сии значение r2 отражает истинную зависимость или
оно получено слу-чайно, применяется процедура проверки гипотез, основанная на анали-зе F-критерия (критерия Фишера):
Слайд 2929
29
Регрессионный анализ
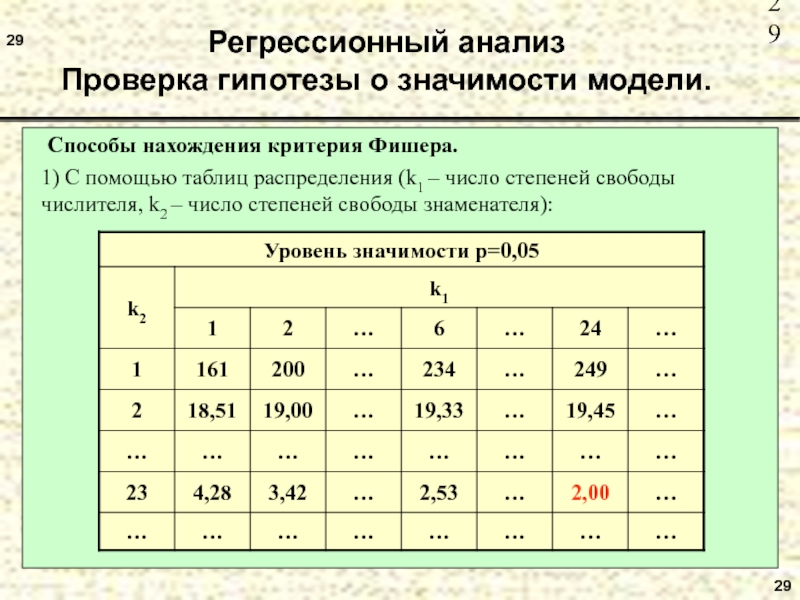
Проверка гипотезы о значимости модели.
Способы нахождения критерия Фишера.
1) С
помощью таблиц распределения (k1 – число степеней свободы числителя, k2
– число степеней свободы знаменателя):
Слайд 3030
Регрессионный анализ
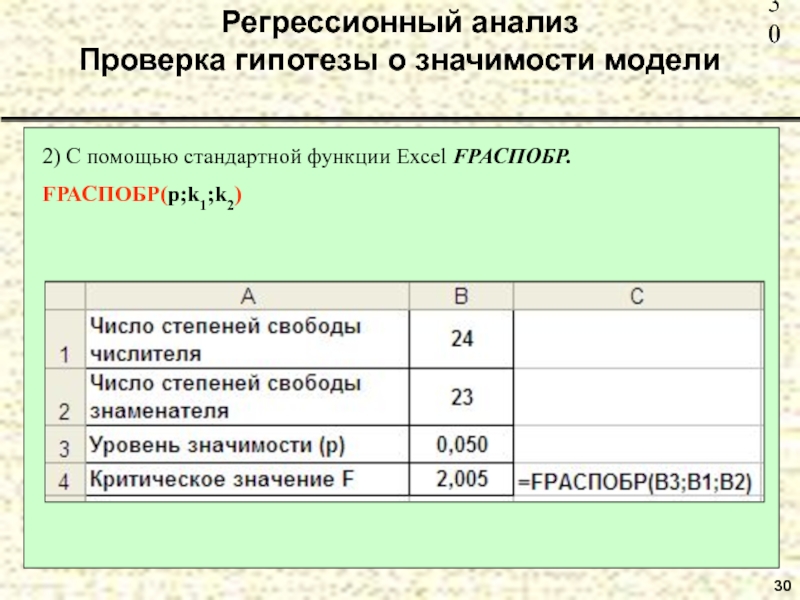
Проверка гипотезы о значимости модели
2) С помощью стандартной функции
Excel FРАСПОБР.
FРАСПОБР(p;k1;k2)
Слайд 3131
Регрессионный анализ
Нелинейная парная регрессия
Пример 10. В таблице приведены данные количества
покупаемых бананов в месяц (кг) от годового дохода (в тыс.
условных единиц) для десяти семей.Построить уравнения линейной и нелинейной регрессии и оценить качество полученных моделей.
Слайд 3333
Регрессионный анализ
Нелинейная парная регрессия
2. Уравнение нелинейной регрессии:
Fp > Fкр -
модель адекватна
Слайд 3434
Регрессионный анализ
Нелинейная парная регрессия
Нелинейные модели парной регрессии и преобразование переменных.
a1
