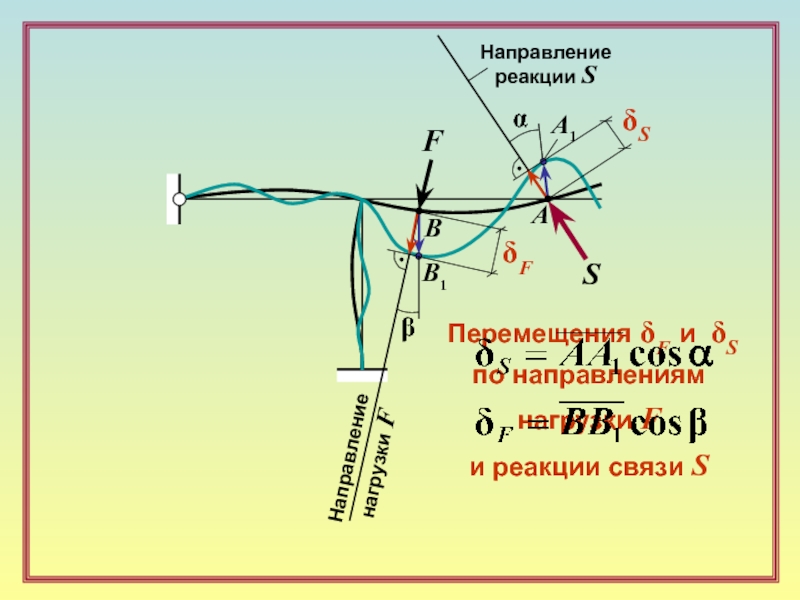
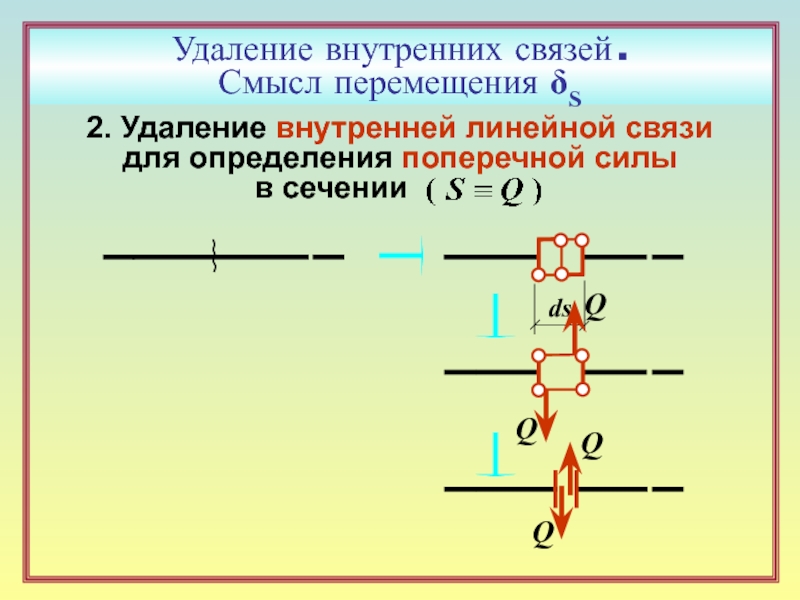
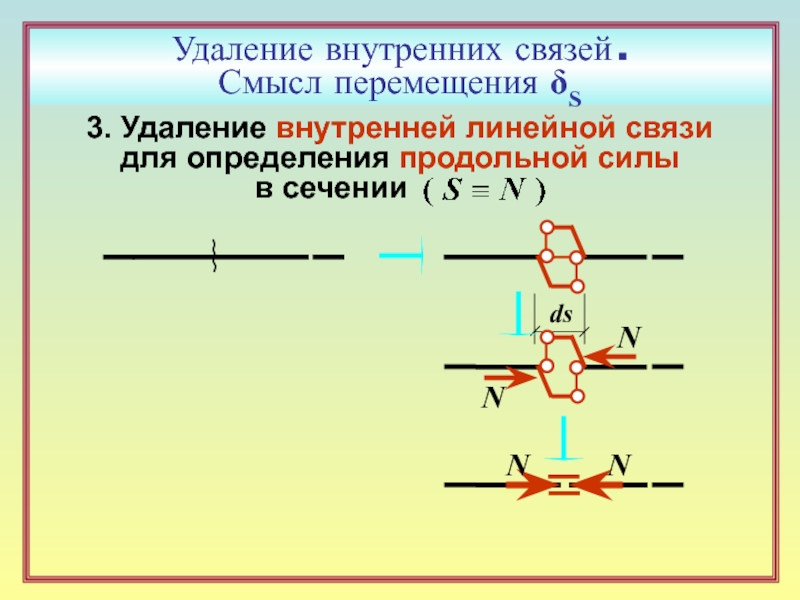
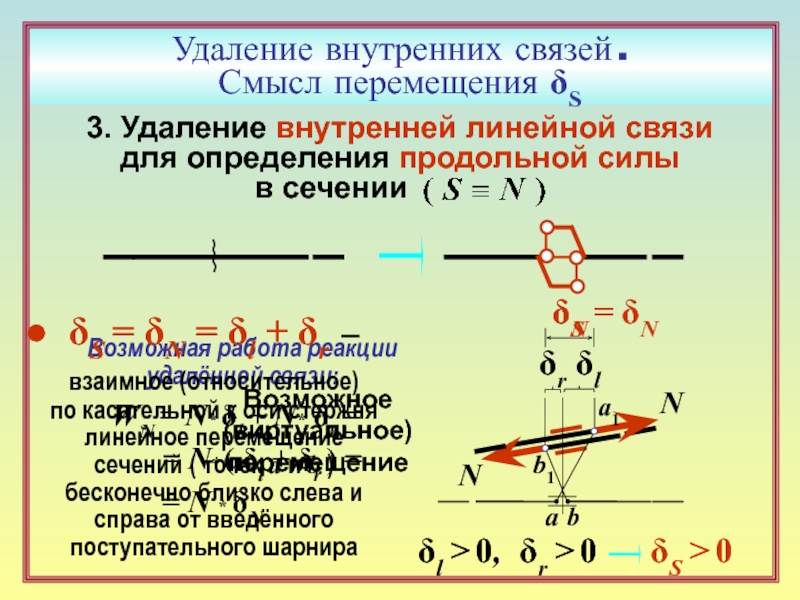
между дисками
в сечениях элементов
(внутренние
силовые факторы)Методы определения
силовых факторов
статический
кинематический
энергетический
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
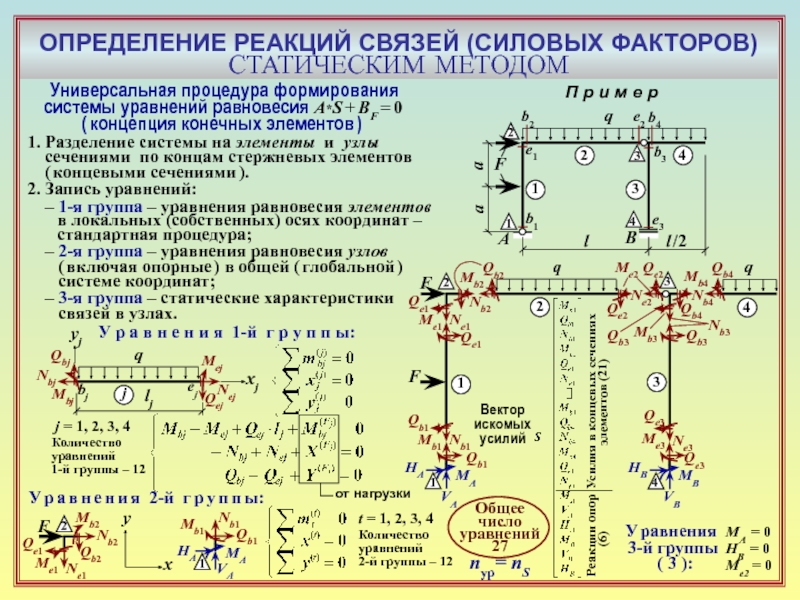
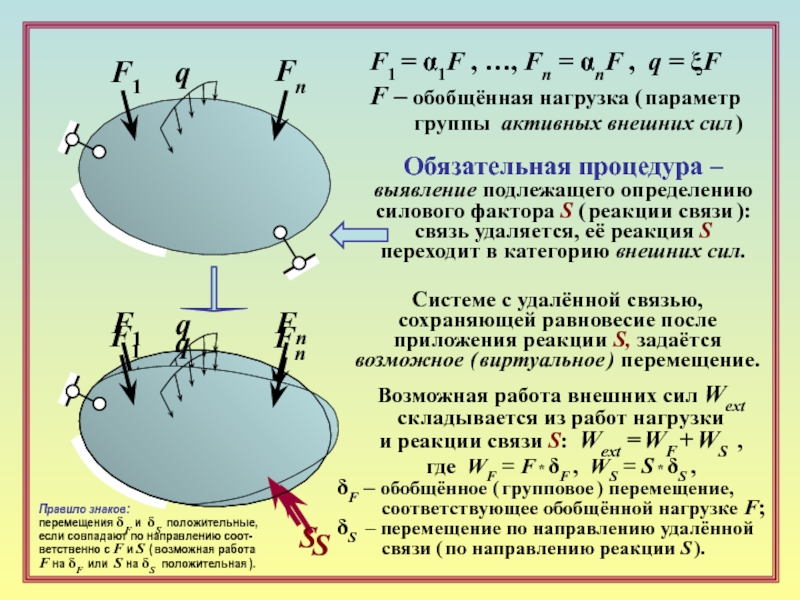
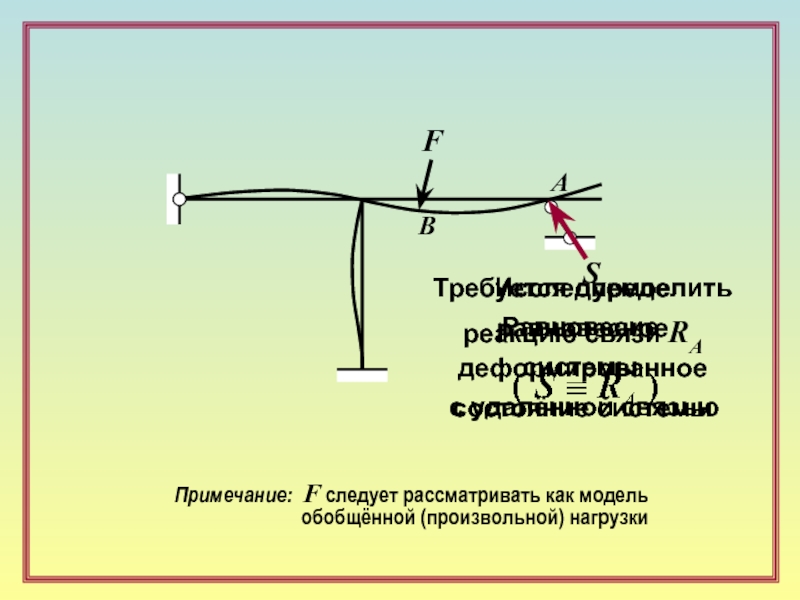
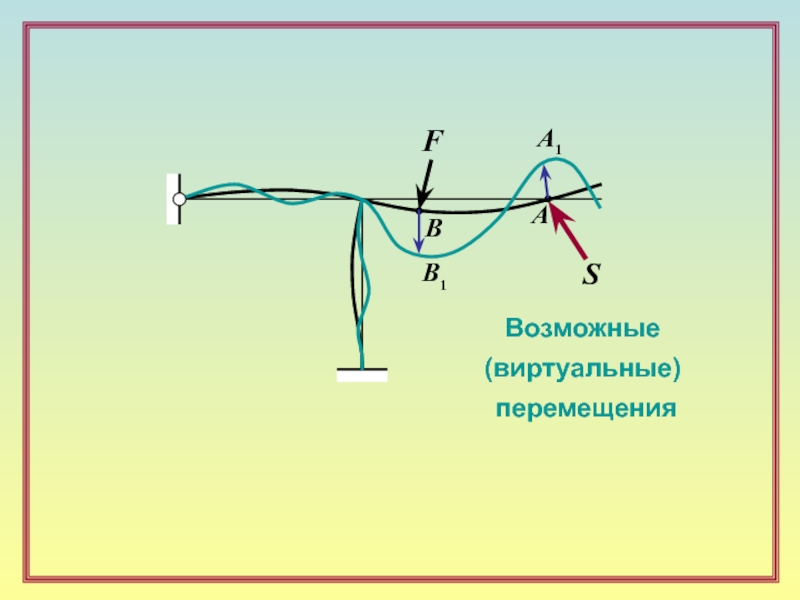
Сущность статического метода – непосредственное использование уравнений равновесия системы в целом и/или её частей.
Уравнения равновесия в случае линейно деформируемой системы:
A*S + BF = 0
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Для системы в целом:
– число искомых усилий nS = nc ;
– количество уравнений nyp= nΔ .
В случае статически определимой
cистемы (W = 0) nΔ=nc nyp= nS
F1
F2
q
M
h
l
l/2
l/2
F1
q
F2
q
A
A
B
B
C
C
C
HA
VA
MA
VC
VC
HC
VB
nΔ= 3*2 = 6 = nyp ;
nc = nS = 6
Вектор искомых
реакций связей:
M
h
l
l/2
l/2