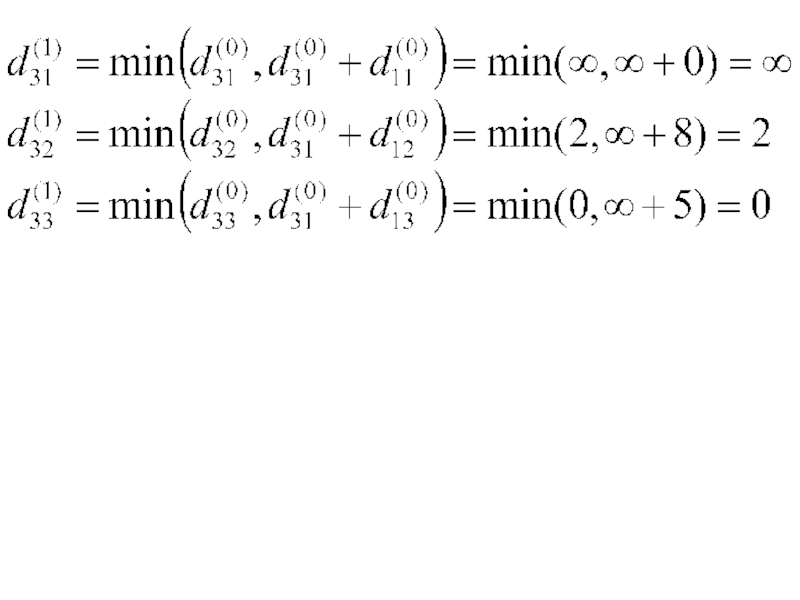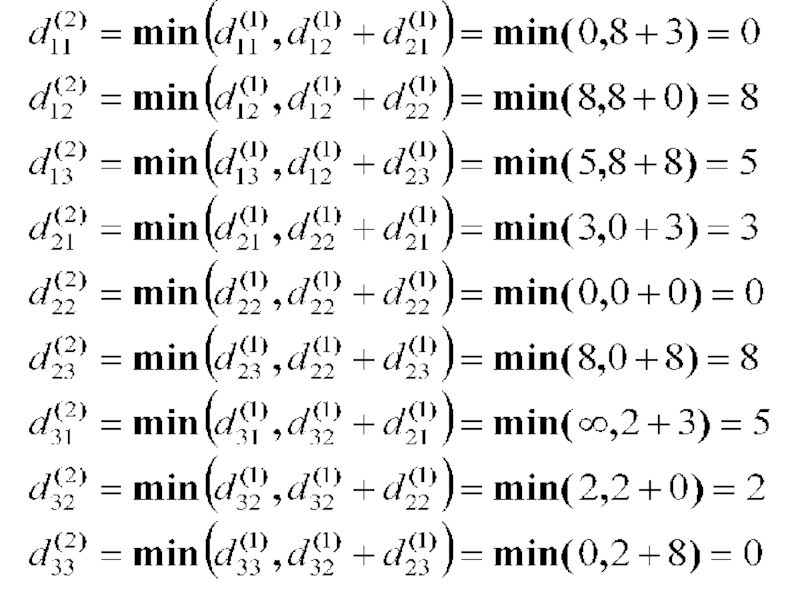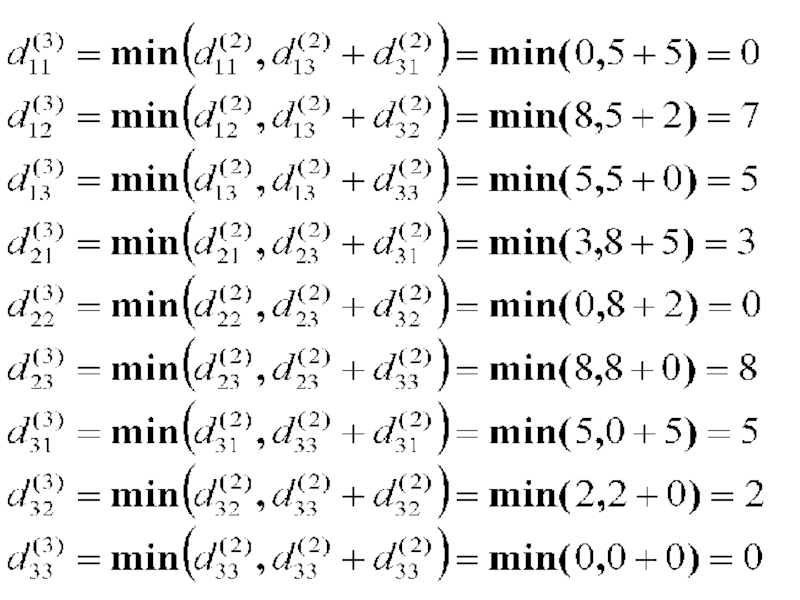Графы.ppt

Содержание

1. Графы.ppt
2. Обозначим через
3. 2)3) Длина кратчайшего пути из вершины vi
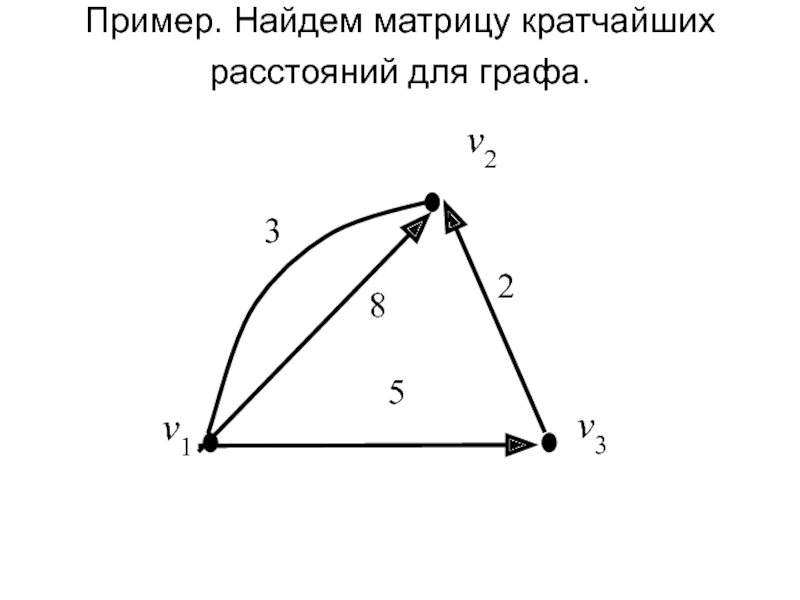
4. Пример. Найдем матрицу кратчайших расстояний для графа. v15
5. v1 v2 v3
6. Элементы матрицы D(1) находим по правилу:
7. Слайд 7
8. Элементы матрицы D(2) находим по правилу:
9. Слайд 9
10. Элементы матрицы D(3) находим по правилу:
11. Слайд 11
12. Слайд 12
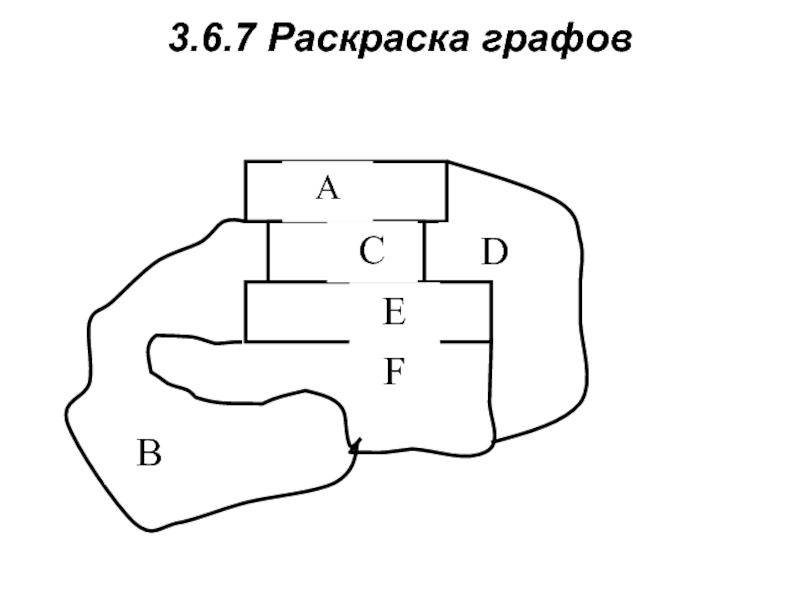
13. 3.6.7 Раскраска графов
14. Слайд 14
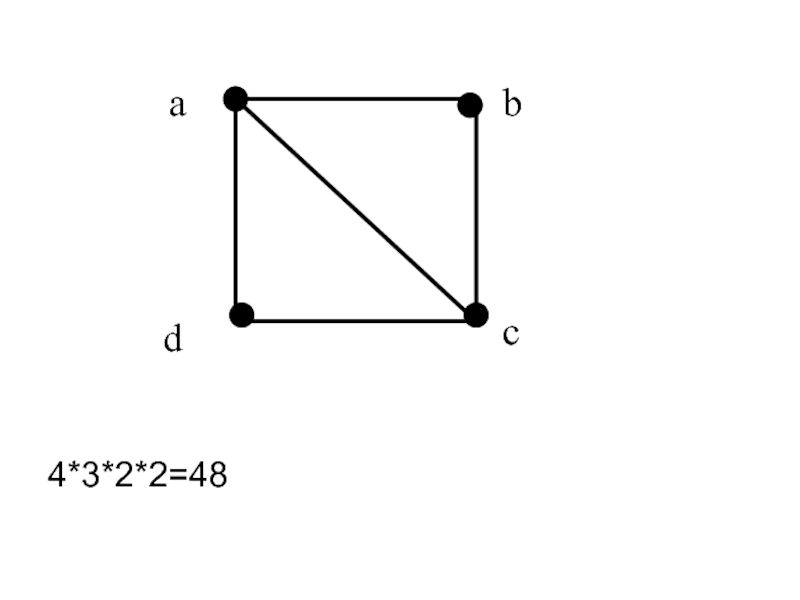
15. 4*3*2*2=48
16. Раскраской графа G называетсяокрашивание вершин графа G,
17. Само λ при этом называется хроматическим числом.
18. Скачать презентанцию

Обозначим через длину кратчайшего пути из vi в vj с промежуточными вершинами во множестве {v1,…,vm}. Алгоритм использует три правила:1)

Слайды и текст этой презентации

Слайд 1Алгоритм Флойда-Уоршалла
Находит кратчайшие расстояния между всеми парами вершин графа
Идея:

Строится специальная матрица D, элементы которой – кратчайшие пути между

всевозможными парами вершин графа G. При определении кратчайшего пути выбирается минимум из «прямого» расстояния между смежными вершинами vi и vj и суммарного расстояния при проходе через дополнительную вершину. Затем – более длинные пути и т.д.

Алгоритм Флойда-Уоршалла Находит кратчайшие расстояния между всеми парами вершин графаИдея: Строится специальная матрица D, элементы которой –

Слайд 2Обозначим через

длину кратчайшего

пути из vi в vj с промежуточными вершинами

во множестве {v1,…,vm}.
Алгоритм использует три правила:
1)
- вес дуги, соединяющей вершины vi и vj (т.е. первоначально матрица D – это исходная матрица весов).

Обозначим через длину кратчайшего пути из vi в vj

Слайд 32)

3) Длина кратчайшего пути из вершины vi в вершину vj:

Алгоритм строит матрицу за n шагов, т.е. строится матрица D(1)

, …, D(n) =D.

2)3) Длина кратчайшего пути из вершины vi в вершину vj: Алгоритм строит матрицу за n шагов, т.е.

Слайд 4Пример. Найдем матрицу кратчайших расстояний для графа.

v1
5

Слайд 5 v1

v2 v3

Слайд 6Элементы матрицы D(1) находим по правилу:

Слайд 7

Слайд 8

Элементы матрицы D(2) находим по правилу:

Слайд 9

Слайд 10

Элементы матрицы D(3) находим по правилу:

Слайд 11

Слайд 12

Слайд 133.6.7 Раскраска графов

Слайд 14

Слайд 15

432*2=48

Слайд 16Раскраской графа G называется
окрашивание вершин графа G, такое, что
никакие две

смежные вершины не окрашены
в один цвет.
Пусть СG(λ) обозначает количество

способов
раскраски графа G с использованием λ
цветов, так, что никакие две соседние
вершины не окрашены в разные цвета. Для
фиксированного графа G это
полиномиальная функция от λ.