Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1_14.ppt
Содержание
- 1. 1_14.ppt
- 2. Периодические граничные условияВ большинстве случаев рассматриваемые конечные
- 3. Решетка БравэПонизить размерность фоковского базиса системы можно,
- 4. Задача ШредингераЗадача Шредингера на периодической решетке:Оператор трансляции
- 5. Задача ШредингераВекторы b называются базисными векторами обратной
- 6. Задача ШредингераСобственную волновую функцию гамильтониана в условиях
- 7. Пример. Одномерная цепочкаОдномерная цепочка из четырех узлов
- 8. Базис оператора трансляцийСобственные функции оператора трансляций могут
- 9. Базис оператора трансляцийМатричные элементы внутри блока, отвечающего
- 10. Спектральный анализРазбиение гамильтоновой матрицы по трансляциям позволяет
- 11. Скачать презентанцию
Периодические граничные условияВ большинстве случаев рассматриваемые конечные системы, кластеры, выбираются с периодическими граничными условиями для того, чтобы все узлы системы были эквивалентнымиДля конкретных случаев может быть выбрана и другая, необязательно периодическая,
Слайды и текст этой презентации
Слайд 1Периодические граничные условия. Решетка Бравэ. Задача Шредингера. Оператор трансляций.
Спектральный анализ
1.14.
Конечные кластеры и трансляционная инвариантность
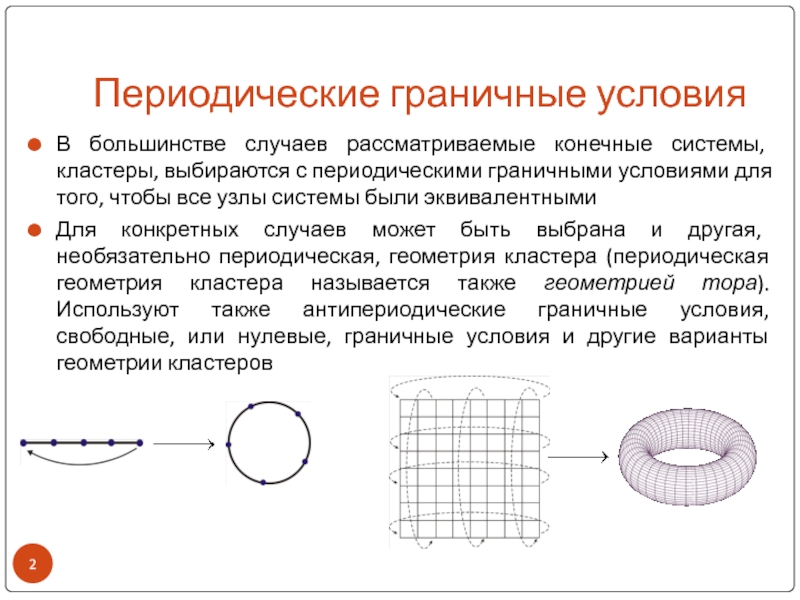
Слайд 2Периодические граничные условия
В большинстве случаев рассматриваемые конечные системы, кластеры, выбираются
с периодическими граничными условиями для того, чтобы все узлы системы
были эквивалентнымиДля конкретных случаев может быть выбрана и другая, необязательно периодическая, геометрия кластера (периодическая геометрия кластера называется также геометрией тора). Используют также антипериодические граничные условия, свободные, или нулевые, граничные условия и другие варианты геометрии кластеров
Слайд 3Решетка Бравэ
Понизить размерность фоковского базиса системы можно, если учесть симметрию
кластера
Вектор трансляции на пространственной периодической структуре:
Периодическая структура с определенным на
ней вектором трансляции называется решеткой БравэВекторы трансляции полностью определяют пространственную решетку Бравэ
Оператор трансляции:
Свойство оператора трансляции:
Слайд 4Задача Шредингера
Задача Шредингера на периодической решетке:
Оператор трансляции коммутирует с гамильтонианом:
Существует
общая система собственных функций для гамильтониана и оператора трансляций:
В общем
случае для каждого базисного вектора решетки:Для вектора трансляции имеем:
Вектор k определен с точностью до вектора g:
Множество таких векторов можно представить в виде разложения
Слайд 5Задача Шредингера
Векторы b называются базисными векторами обратной решетки и обычно
выбираются в виде:
Для простой кубической решетки:
Базисные вектора обратной решетки ортогональны
базисным векторам прямой решетки:Оператор трансляций может быть записан в виде:
Оператор трансляции унитарен:
Слайд 6Задача Шредингера
Собственную волновую функцию гамильтониана в условиях периодического потенциала можно
представить как произведение экспоненциального множителя на периодическую функцию (теорема Блоха):
Граничные
условия Борна – Кармана:Разрешенные значения блоховского волнового вектора k действительны:
Для простой кубической решетки:
Решение задачи Шредингера, которое удовлетворяет трансляционной инвариантности, следует искать в виде блоховской волновой функции, при этом вектор k является одним из разрешенных векторов обратной решетки
Слайд 7Пример. Одномерная цепочка
Одномерная цепочка из четырех узлов с тремя частицами,
описываемая моделью Бозе – Хаббарда. Узельный базис состоит из 20
функций:Сортировка базисных функций на классы; в каждом классе узельные функции порождаются производящей функцией:
Имеем пять классов по четыре функции:
Слайд 8Базис оператора трансляций
Собственные функции оператора трансляций могут быть записаны в
виде комбинаций периодической функции и экспоненциального множителя:
Коэффициенты определяются из условия
ортонормированности:Новый базис представляет собой блочную структуру, пронумерованную по разрешенным векторам обратной решетки (или секторам импульса). Гамильтонова матрица в новом базисе будет блочно-диагональной:
Слайд 9Базис оператора трансляций
Матричные элементы внутри блока, отвечающего сектору m:
С учетом
трансляционной симметрии гамильтониана и узельных функций:
Матричные элементы от диагональной части
гамильтониана:Все матричные элементы недиагональной части гамильтониана внутри блока в общем случае являются ненулевыми, в том числе и элементы на главной диагонали:
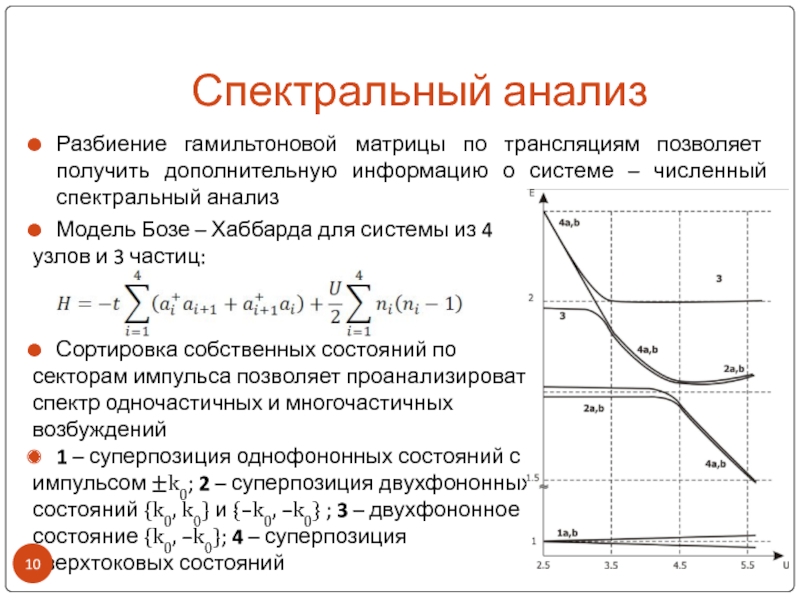
Слайд 10Спектральный анализ
Разбиение гамильтоновой матрицы по трансляциям позволяет получить дополнительную информацию
о системе – численный спектральный анализ
Модель Бозе – Хаббарда для
системы из 4узлов и 3 частиц:
Сортировка собственных состояний по
секторам импульса позволяет проанализировать
спектр одночастичных и многочастичных
возбуждений
1 – суперпозиция однофононных состояний с
импульсом ±k0; 2 – суперпозиция двухфононных
состояний {k0, k0} и {–k0, –k0} ; 3 – двухфононное
состояние {k0, –k0}; 4 – суперпозиция
сверхтоковых состояний