Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Lektsia_2.ppt
Содержание
- 1. Lektsia_2.ppt
- 2. План лекции
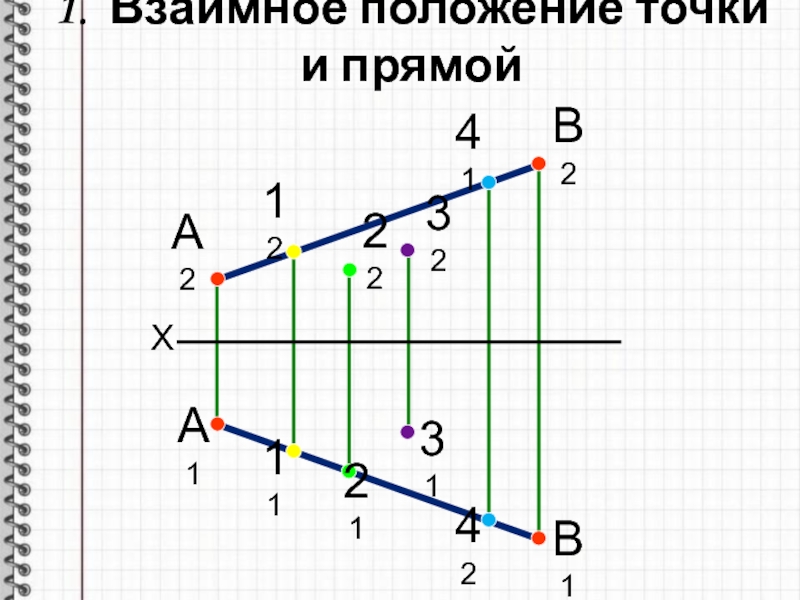
- 3. 1. Взаимное положение точки и прямойXА2В2А1В11211222132314241
- 4. Если точка принадлежит прямой, то проекции точки
- 5. 2.
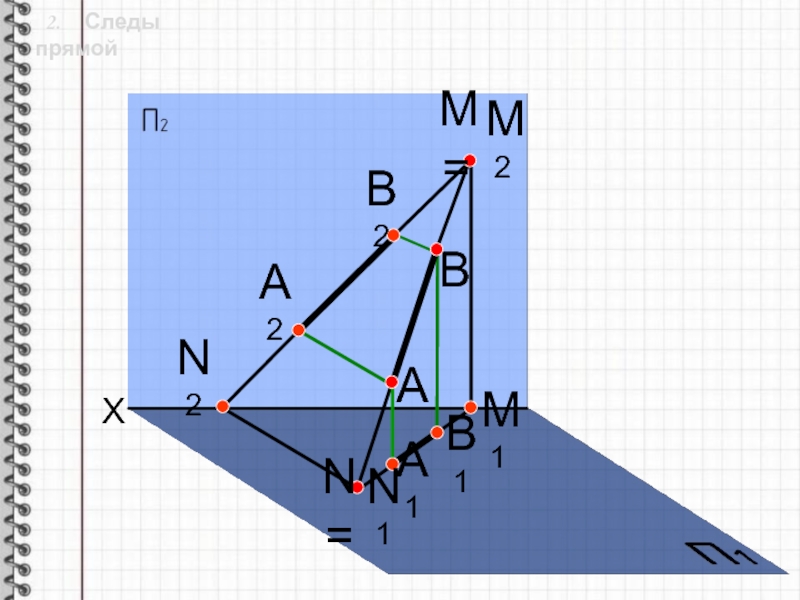
- 6. 2. Следы прямойXА1ВАВ1А2В2N=N1N2M2M=M1
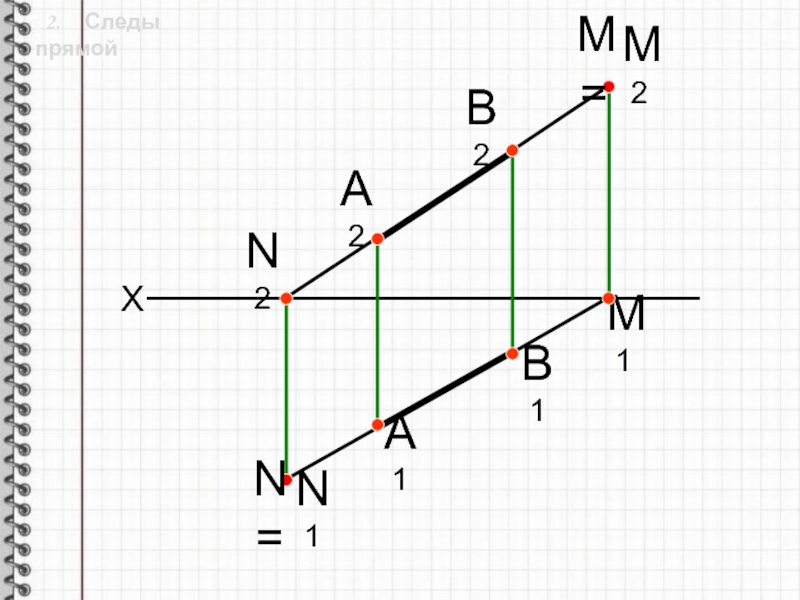
- 7. 2. Следы прямойА1В1А2N=N1N2M2M1B2XM=
- 8. 3. Способ замены плоскостей проекцийСпособ замены
- 9. 3. Способ замены плоскостей
- 10. 3. Способ замены плоскостей проекцийXП2П1А1АА2П4Х1А4ΔΖΔΖΔΖ
- 11. 3. Способ замены плоскостей проекцийXП2П1П4Х1
- 12. 3. Способ замены плоскостей проекцийXП2П1Х1П4
- 13. 3. Способ замены плоскостей проекцийXП2П1Х1П4
- 14. 3. Способ замены плоскостей проекцийXП2Х1П1П4А1А2ZАZАА4
- 15. 3. Способ замены плоскостей проекцийXП2Х1П1П4А1А2ZАZАА4
- 16. 4. Преобразование чертежа прямойПрямая общего положения может быть преобразована в:1. Прямую уровня2. Проецирующую прямую
- 17. 4. Преобразование чертежа прямойПреобразование прямой общего положения в прямую уровняXП2Х1П1П4А1А2ZАZАВ4В1В2А4П1ZВZВН.В.
- 18. 4. Преобразование чертежа прямойПреобразование прямой уровня в проецирующую прямуюXП2Х1П1П4А1А2А4=В4В1В2П1ZА=ZВZА=ZВН.В.
- 19. 4. Преобразование чертежа прямойПреобразование прямой общего положения в проецирующую прямуюXП2Х1П1П4C1С2ZCZCD4D1D2C4П1ZDZDН.В.Х2П5C5=D5П4YC=YDYC=YD
- 20. 5. Взаимное положение двух прямыхПрямые в пространстве могут быть: пересекающимися; скрещивающимися; параллельными(в частности совпадать).
- 21. 5. Взаимное положение двух
- 22. 5. Взаимное положение двух
- 23. 5. Взаимное положение двух
- 24. 5. Взаимное положение двух
- 25. 5. Взаимное положение двух прямыхXПараллельны ли данные прямые?ZYB1B2A1D1C1D2C2A2A3B3C3D3Прямые AB и CD не параллельны.
- 26. 6.
- 27. 6. Проекции плоских углов.«Прямой
- 28. 6. Проекции плоских углов.Теорема о прямом углеП1D1DК1Дано:Доказать:Доказательство:QЕКЕ1
- 29. доценты кафедры «Начертательная геометрия, инженерная и компьютерная
- 30. Скачать презентанцию
Слайды и текст этой презентации
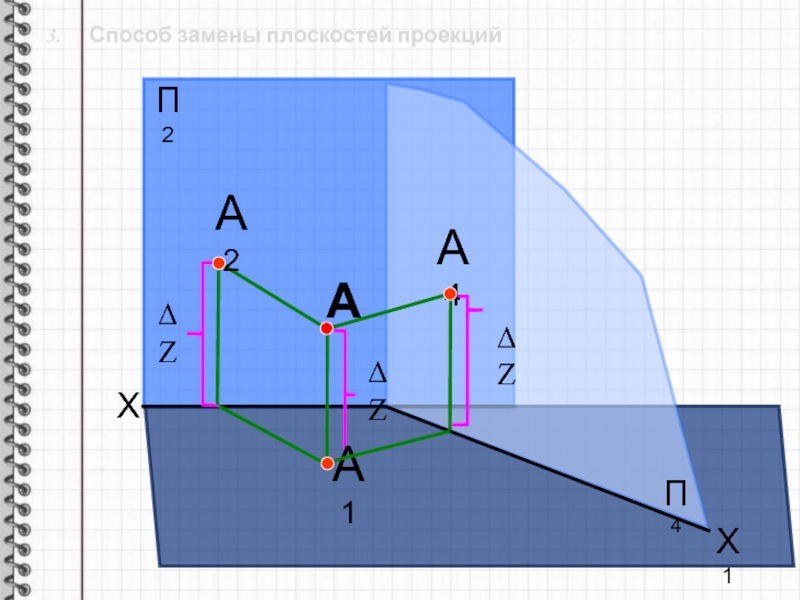
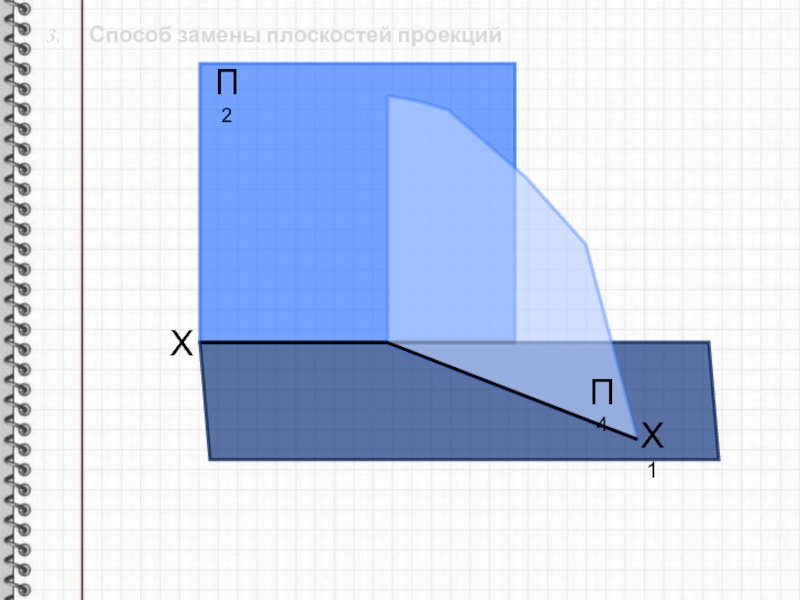
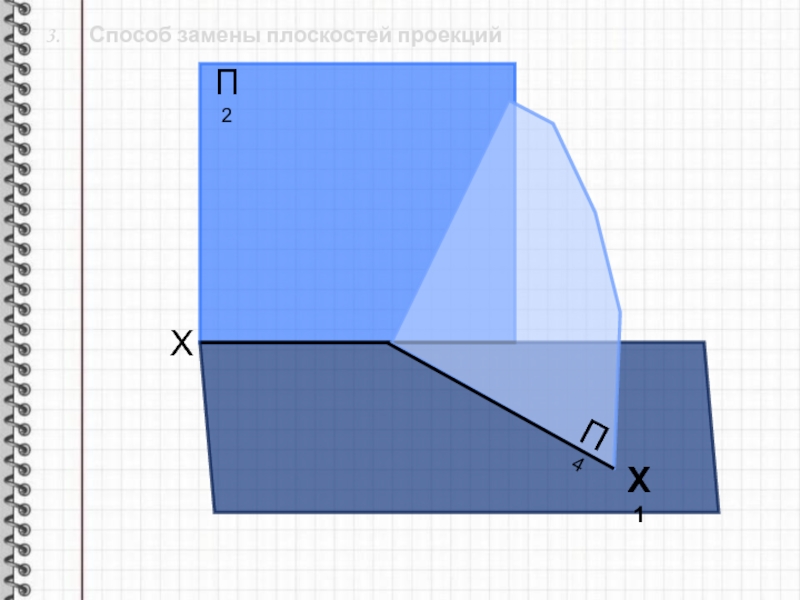
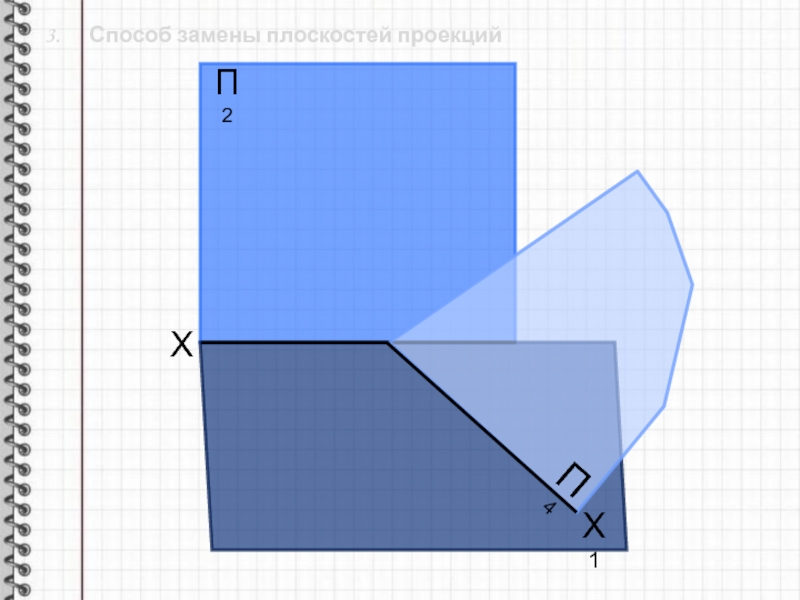
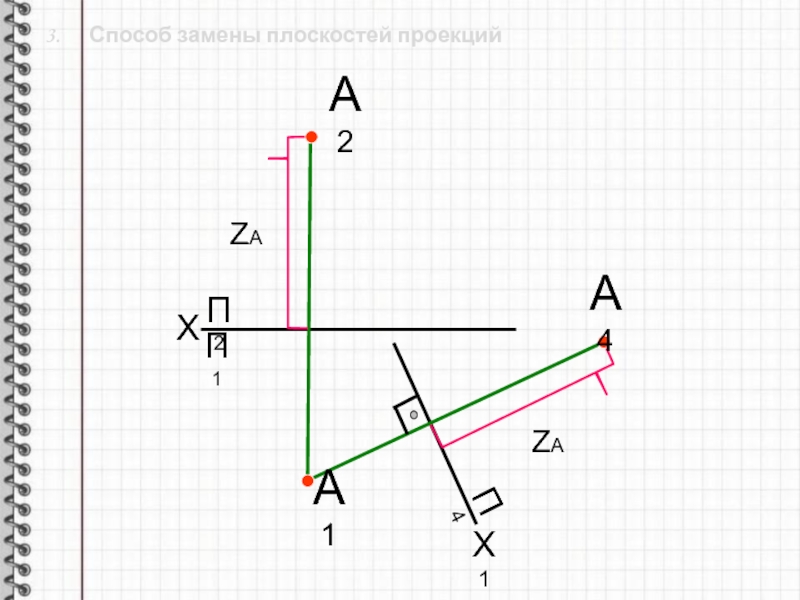
Слайд 83. Способ замены плоскостей проекций
Способ замены плоскостей проекций заключается
в последовательной замене одной из плоскостей проекций на другую.
Геометрическая фигура
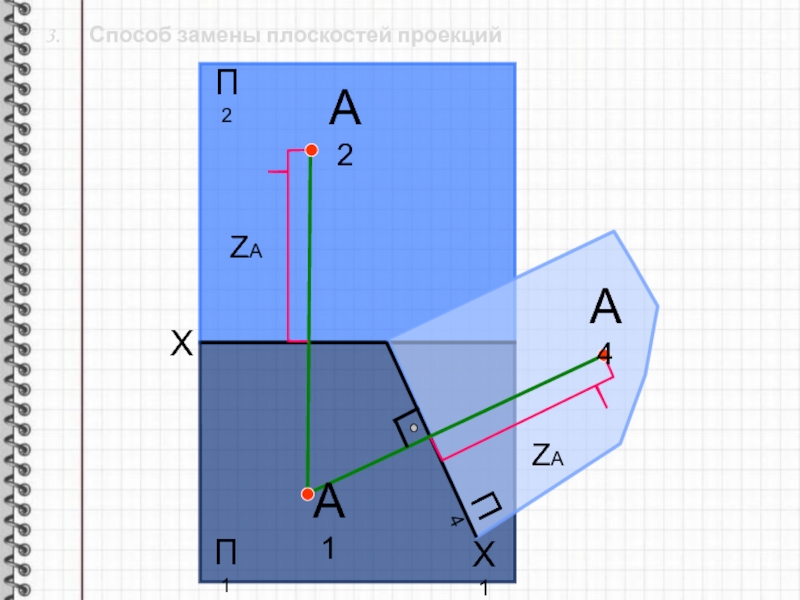
своего положения не меняет. Слайд 9 3. Способ замены плоскостей проекций
При этом должны
быть выдержаны следующие условия:
1. Новая плоскость должна быть перпендикулярна не
заменяемой плоскости проекций;2. На новую плоскость проекций геометрическая фигура проецируется ортогонально.
Слайд 164. Преобразование чертежа прямой
Прямая общего положения может быть
преобразована в:
1. Прямую уровня
2. Проецирующую прямую
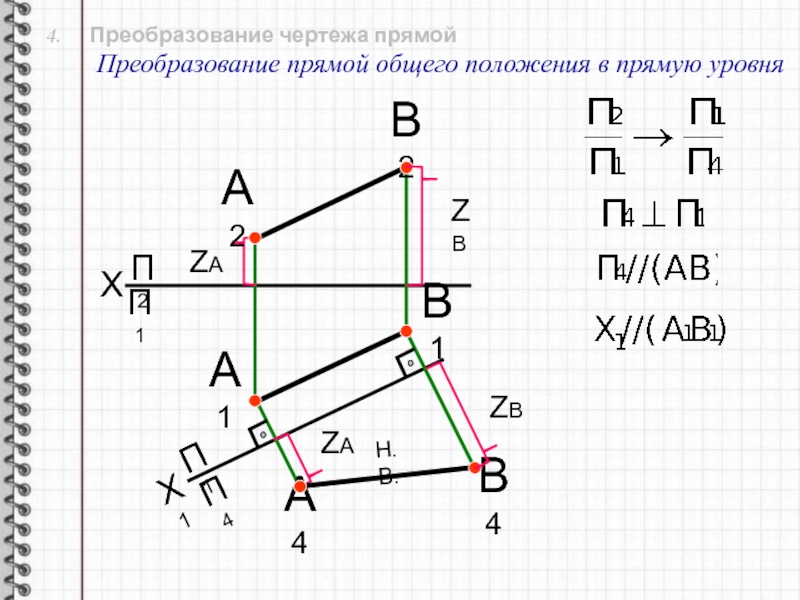
Слайд 17 4. Преобразование чертежа прямой
Преобразование прямой общего положения
в прямую уровня
X
П2
Х1
П1
П4
А1
А2
ZА
ZА
В4
В1
В2
А4
П1
ZВ
ZВ
Н.В.
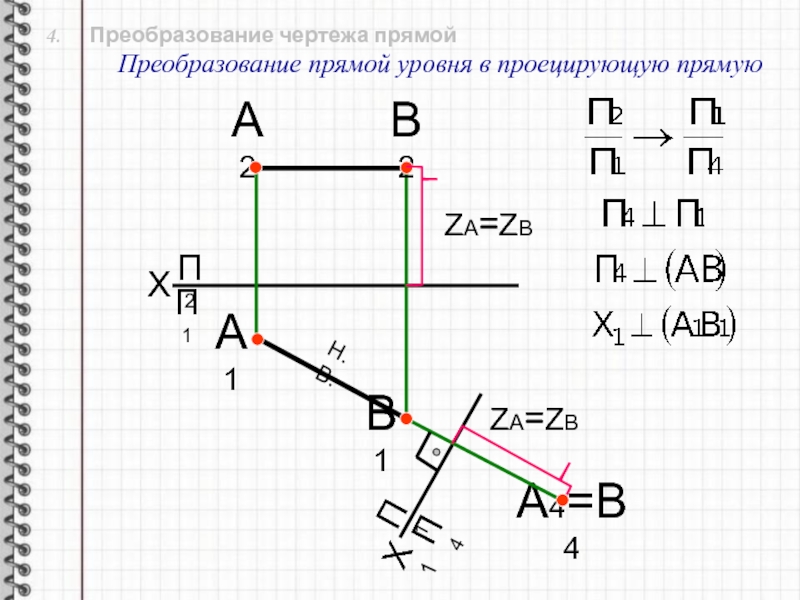
Слайд 18 4. Преобразование чертежа прямой
Преобразование прямой уровня в
проецирующую прямую
X
П2
Х1
П1
П4
А1
А2
А4=В4
В1
В2
П1
ZА=ZВ
ZА=ZВ
Н.В.
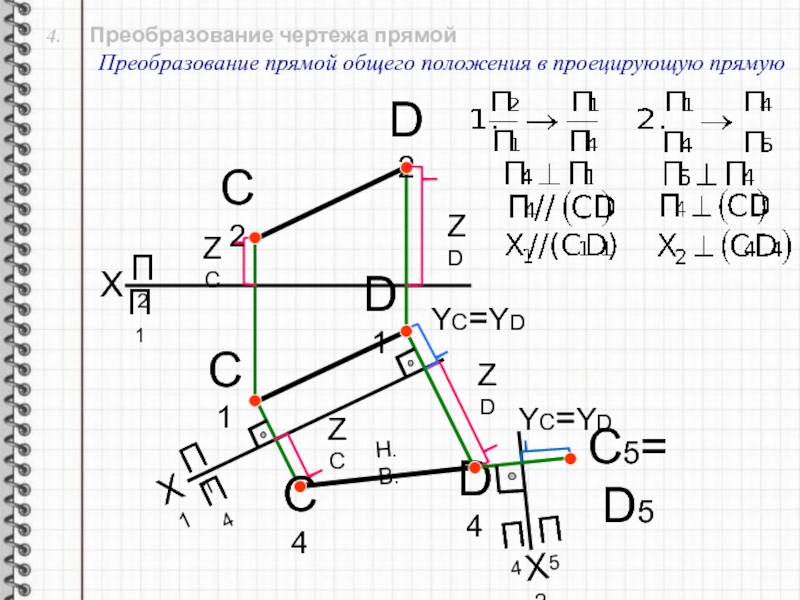
Слайд 19 4. Преобразование чертежа прямой
Преобразование прямой общего положения
в проецирующую прямую
X
П2
Х1
П1
П4
C1
С2
ZC
ZC
D4
D1
D2
C4
П1
ZD
ZD
Н.В.
Х2
П5
C5=D5
П4
YC=YD
YC=YD
Слайд 205. Взаимное положение двух прямых
Прямые в пространстве могут быть:
пересекающимися;
скрещивающимися;
параллельными
(в частности совпадать).
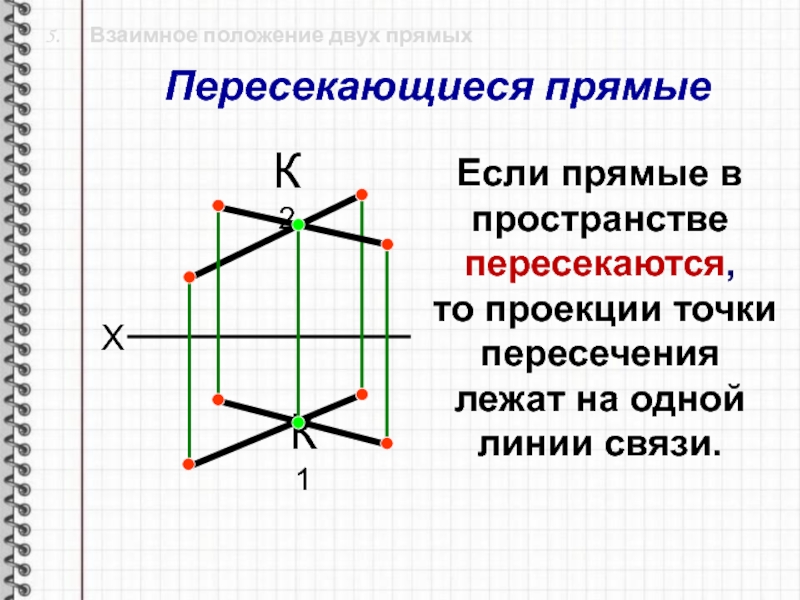
Слайд 21 5. Взаимное положение двух прямых
К1
К2
X
Если прямые в
пространстве
пересекаются,
то проекции точки пересечения лежат на одной линии
связи.Пересекающиеся прямые
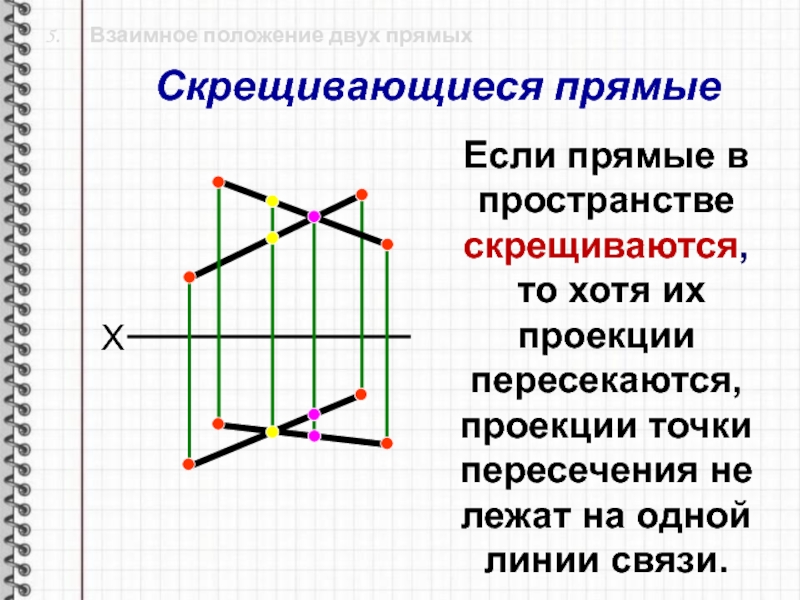
Слайд 22 5. Взаимное положение двух прямых
X
Если прямые в
пространстве
скрещиваются,
то хотя их проекции пересекаются, проекции точки пересечения
не лежат на одной линии связи.Скрещивающиеся прямые
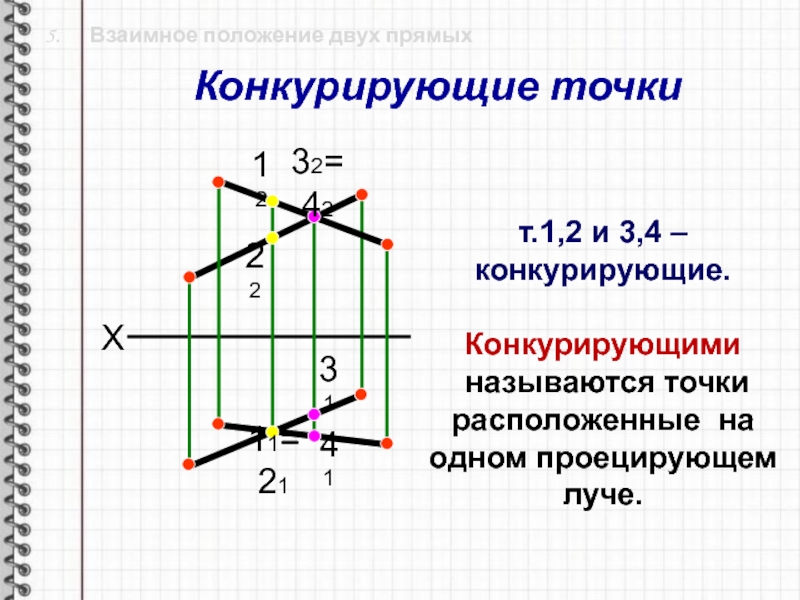
Слайд 23 5. Взаимное положение двух прямых
X
т.1,2 и 3,4
– конкурирующие.
Конкурирующими
называются точки расположенные на одном проецирующем
луче.Конкурирующие точки
12
11=21
41
31
22
32=42
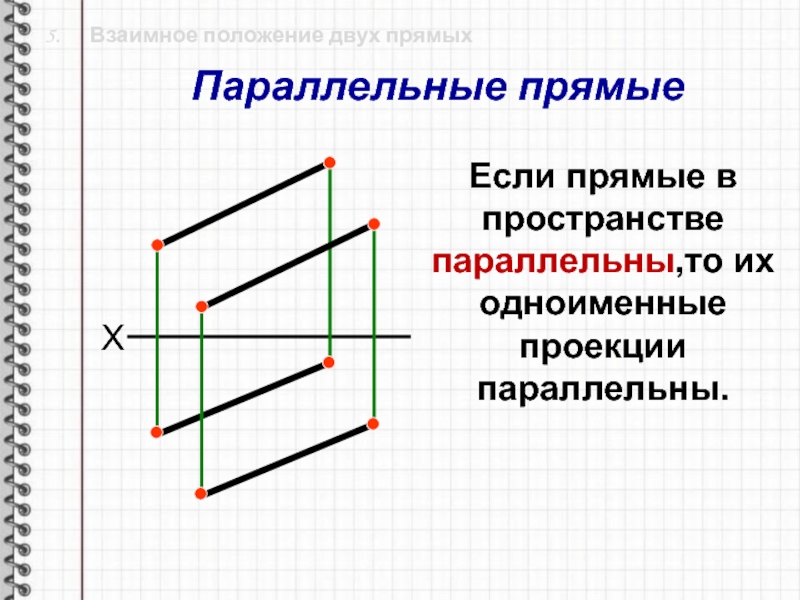
Слайд 24 5. Взаимное положение двух прямых
X
Если прямые в
пространстве параллельны,то их одноименные проекции параллельны.
Параллельные прямые
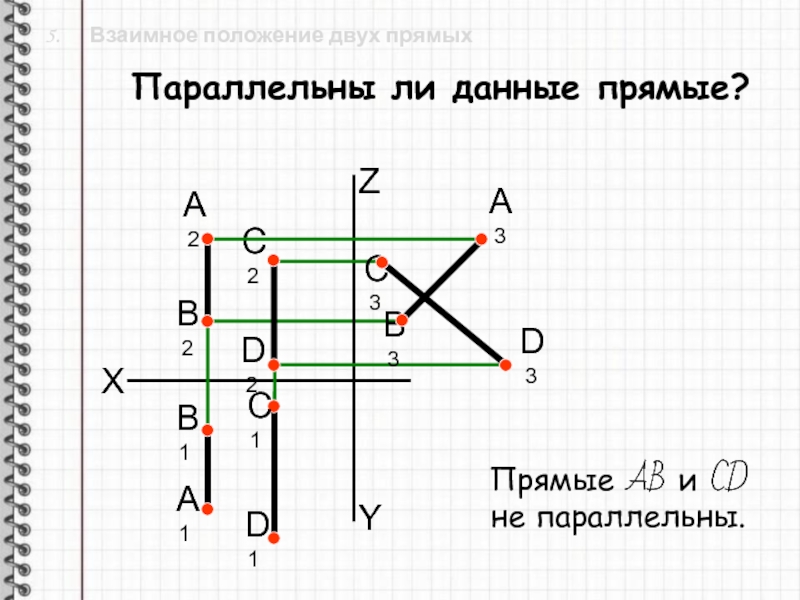
Слайд 25 5. Взаимное положение двух прямых
X
Параллельны ли данные
прямые?
Z
Y
B1
B2
A1
D1
C1
D2
C2
A2
A3
B3
C3
D3
Прямые AB и CD не параллельны.
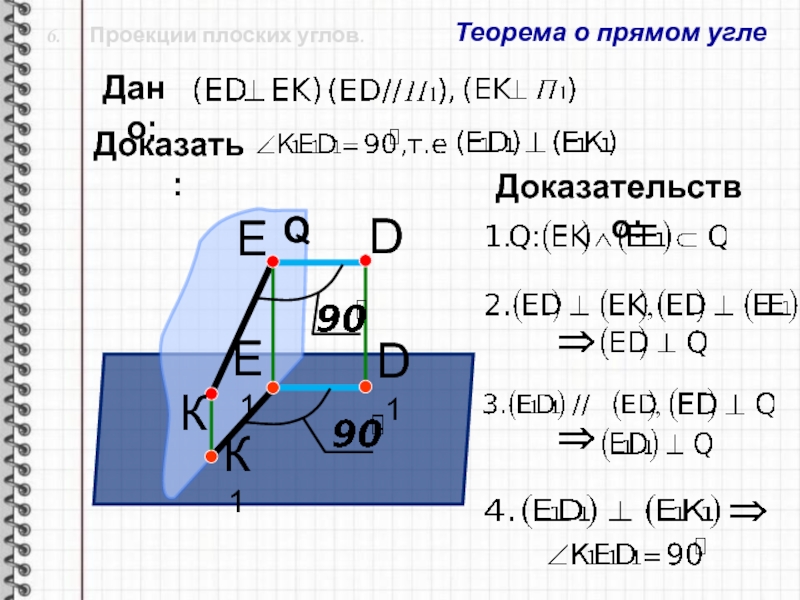
Слайд 266. Проекции плоских углов
В
зависимости от положения сторон плоского угла по отношению к плоскости
проекций он может проецироваться в угол от 0º до 180º.Если стороны угла параллельны плоскости, то на эту плоскость угол проецируется в натуральную величину.
Слайд 27
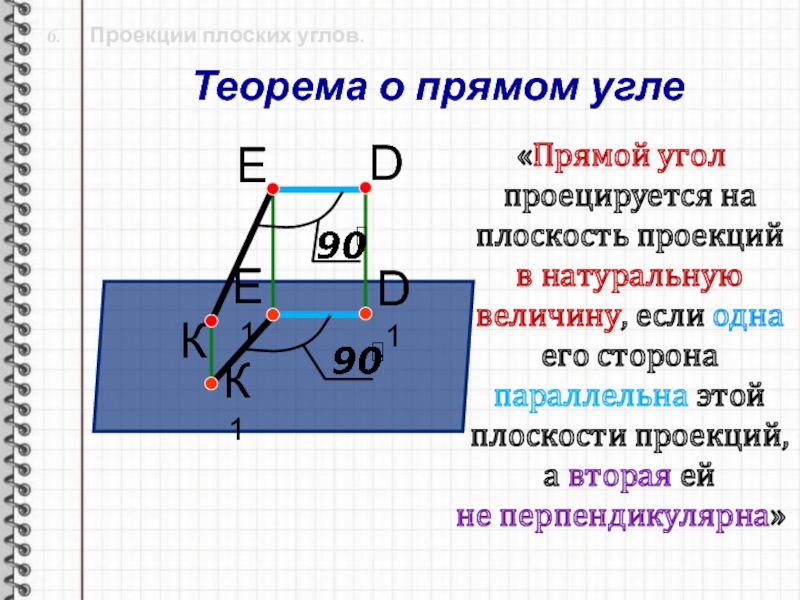
6. Проекции плоских углов.
«Прямой угол проецируется на
плоскость проекций в натуральную величину, если одна его сторона параллельна
этой плоскости проекций, а вторая ейне перпендикулярна»
Теорема о прямом угле
К1
П1
D1
Е1
К
D
Е
Слайд 29доценты кафедры «Начертательная геометрия, инженерная и компьютерная графика» Омского Государственного
технического университета:
Бондарев Олег Александрович, к.т.н.,
Кайгородцева Наталья Викторовна, к.пед.н.
Авторы: