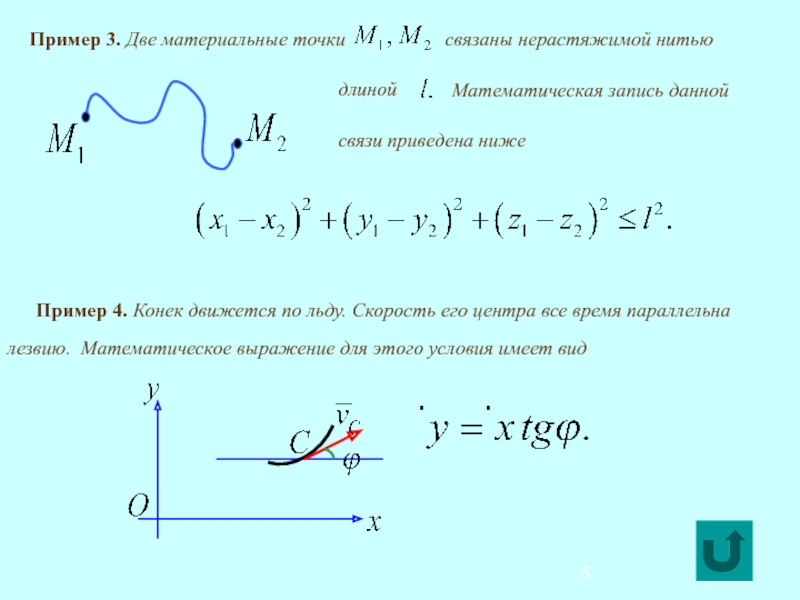
Классификация связей.
2. ОГРАНИЧЕНИЯ, НАЛАГАЕМЫЕ СВЯЗЯМИ
2.1. Возможные положения, скорости и
ускорения. 2.2. Возможные и действительные перемещения.
2.3. Виртуальные перемещения.
2.4. Варьирование по Журдену и Гауссу.