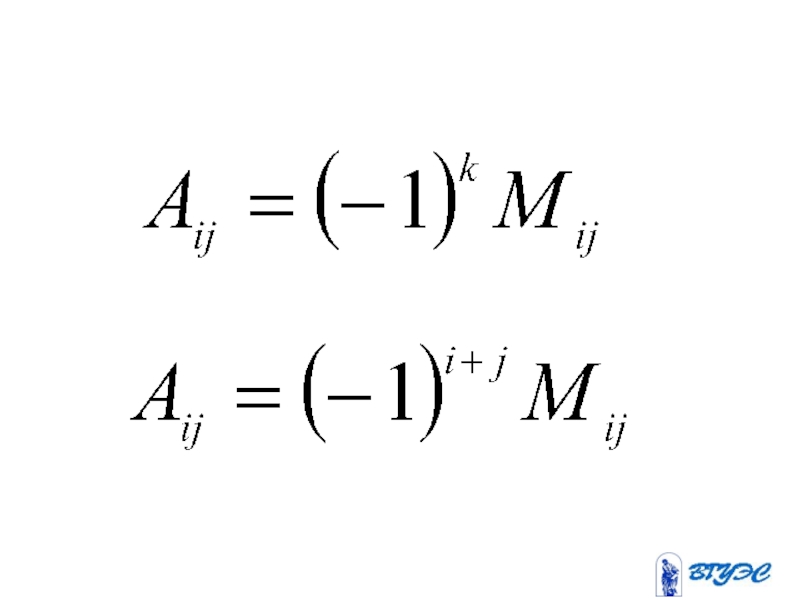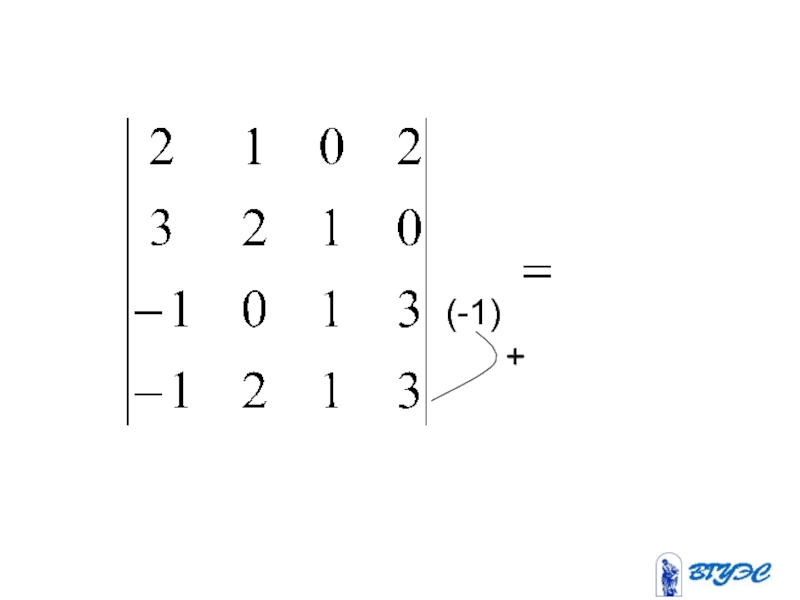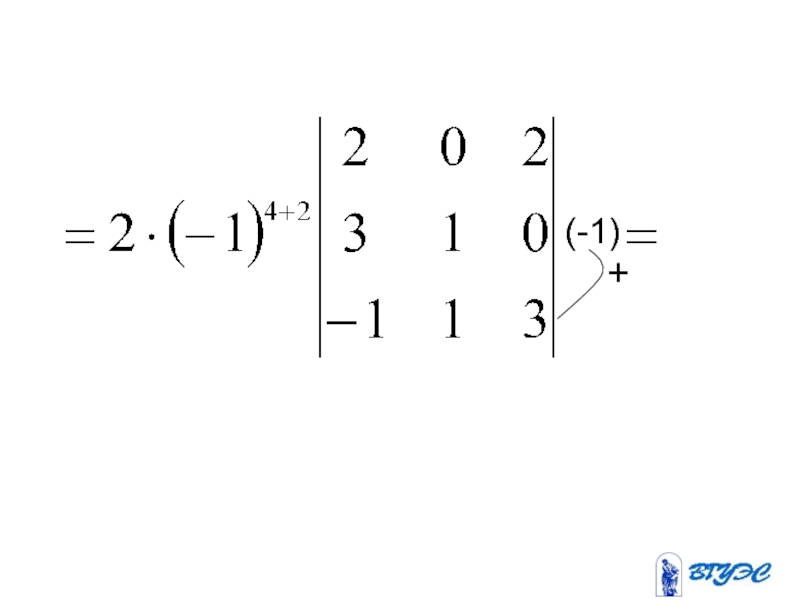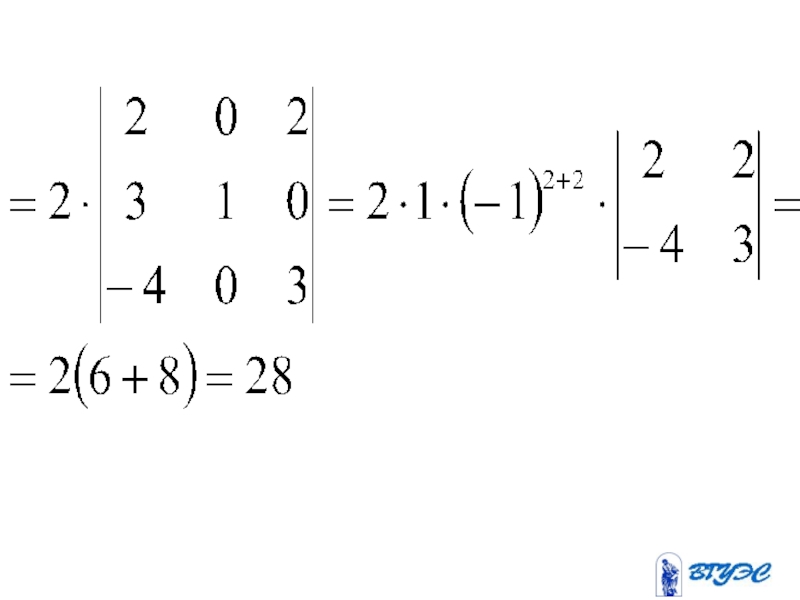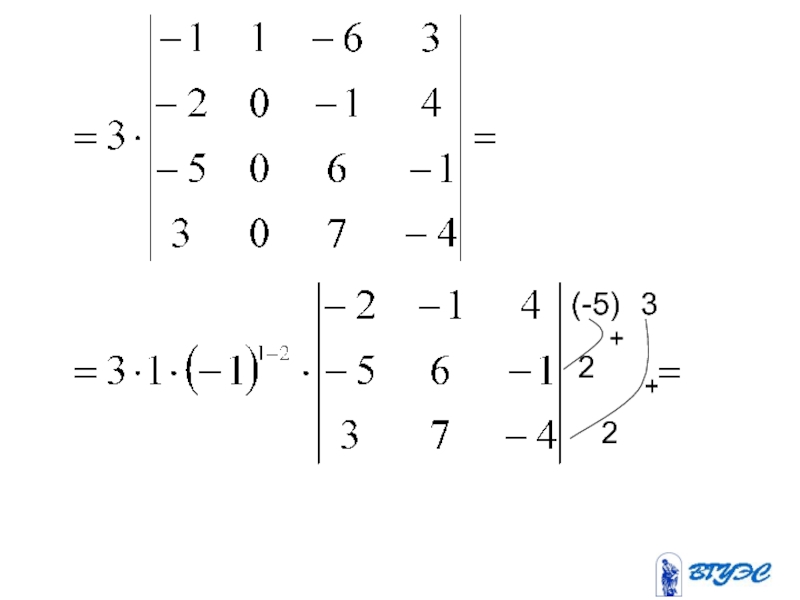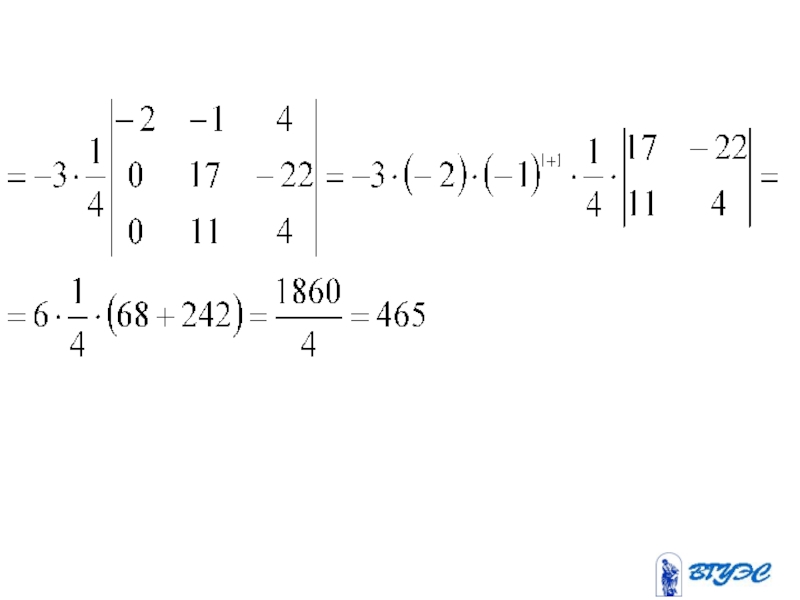Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определители
Содержание
- 1. Определители
- 2. Содержание1. Определители2. Элементы теории матриц3. Системы линейных
- 3. Определители
- 4. Рассмотрим таблицу
- 5. Числа
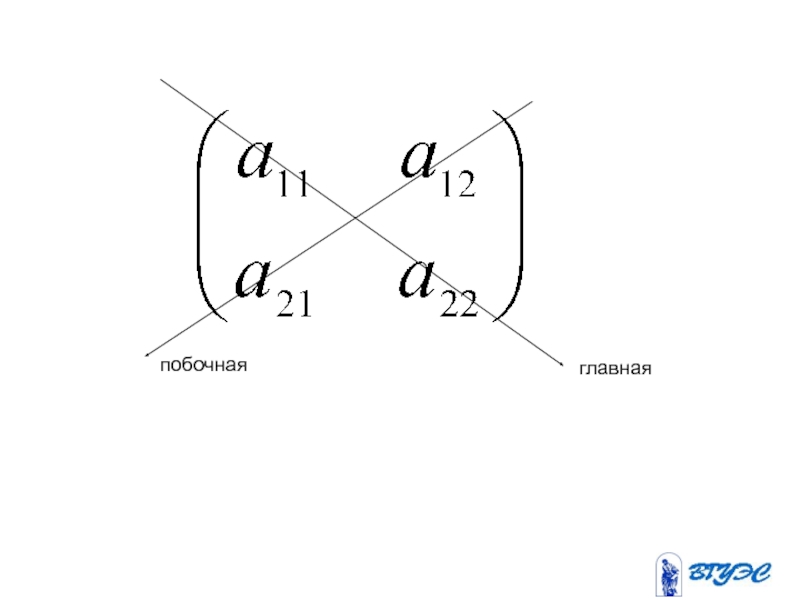
- 6. Число строк – порядок таблицы.Главная диагональ –
- 7. побочнаяглавная
- 8. Выражениеназывается определителем 2-го порядка .
- 9. Определители третьего порядка
- 10. Рассмотрим таблицу
- 11. Выражение виданазывается определителем третьего порядка
- 12. Методы вычисления определителей третьего порядка
- 13. Правило треугольника
- 14. Три произведения элементов, стоящих на главной диагонали
- 15. Разложение по элементам какой-либо строки(столбца)
- 16. Минор
- 17. Опр. Минором элемента определителя 3-го порядка
- 18. Обозначение минора Минор элемента , стоящего на пересечении i-й строки и j-го столбца определителя, обозначают
- 19. Алгебраическое дополнение
- 20. Опр. Алгебраическим дополнениемэлемента определителя
- 21. Слайд 21
- 22. Теорема разложения Определитель 3-го порядка равенсумме произведений элементовкакой-либо строки (столбца)определителя на ихалгебраические дополнения.
- 23. Таким образом, имеет место шесть разложений:
- 24. Свойства определителей1.Определитель не меняет своегозначения при
- 25. 3.Общий множитель элементовкакого-либо строки (столбца) определителяможно
- 26. 6. Значение определителя не
- 27. Определители высших порядков
- 28. Выражениеназывается определителем 4-го порядка
- 29. С помощью свойства 6 добиваются того, чтобы
- 30. (-1)+
- 31. Слайд 31
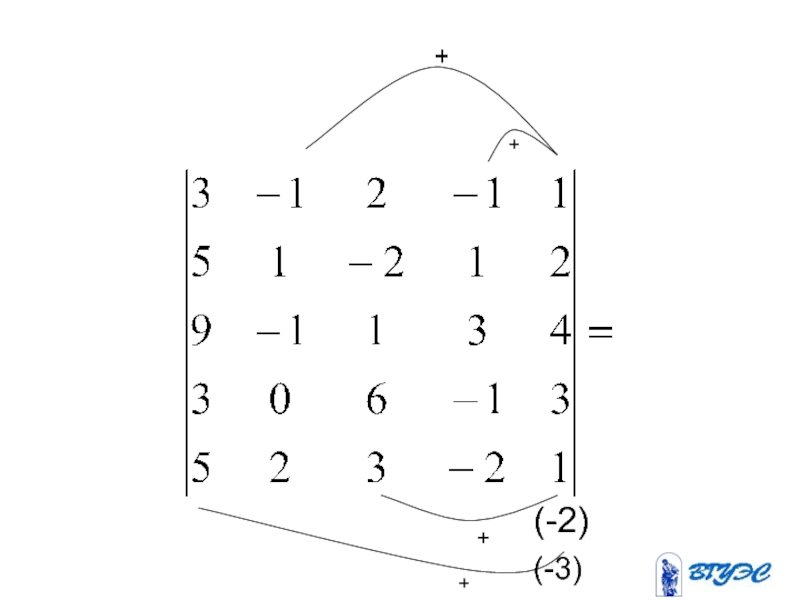
- 32. (-1)+
- 33. Слайд 33
- 34. (-2)(-3)++++
- 35. Слайд 35
- 36. (-1)+++
- 37. (-5)232++
- 38. Слайд 38
- 39. Метод приведения к
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Скачать презентанцию
Содержание1. Определители2. Элементы теории матриц3. Системы линейных уравнений4. Элементы векторной алгебры5. Прямые и плоскости6. Кривые второго порядка7. Комплексные числа
Слайды и текст этой презентации
Слайд 2Содержание
1. Определители
2. Элементы теории матриц
3. Системы линейных уравнений
4. Элементы векторной
алгебры
5. Прямые и плоскости
6. Кривые второго порядка
7. Комплексные числа
Слайд 6Число строк – порядок таблицы.
Главная диагональ – диагональ идущая с
левого верхнего угла в правый нижний.
Побочная диагональ – диагональ идущая
с верхнего правого угла в левый нижний.Слайд 14
Три произведения элементов, стоящих на
главной диагонали и в вершинах
двух
треугольников:
берутся со знаком "+", а три произведения
элементов, стоящих
на побочной диагонали и в вершинах двух других треугольников:
берутся со знаком "−".
Слайд 17
Опр. Минором элемента определителя
3-го порядка называется определитель
2-го
порядка, получающийся из данного
определителя вычёркиванием строки и
столбца, в которых
расположен элемент.
Слайд 18Обозначение минора
Минор элемента , стоящего на
пересечении i-й строки
и j-го
столбца определителя,
обозначают
Слайд 20Опр. Алгебраическим дополнением
элемента определителя 3-го
порядка
называется минор
этого элемента, умноженный
на (-1) в степени , где
Слайд 22Теорема разложения
Определитель 3-го порядка равен
сумме произведений элементов
какой-либо строки (столбца)
определителя
на их
алгебраические дополнения.
Слайд 24 Свойства определителей
1.Определитель не меняет своего
значения при замене каждой строки
соответствующим
столбцом.
2.Определитель изменит знак ,если
поменять местами любые две
строки или столбца.
Слайд 25 3.Общий множитель элементов
какого-либо строки (столбца) определителя
можно выносить за знак
определителя.
4.Определитель равен нулю, если он
имеет два одинаковых столбца или
двеодинаковые строки.
5.Определитель равен нулю, если элементы
какой-либо строки (столбца) все равны нулю.
Слайд 266. Значение определителя не
изменится, если
к элементам строки
или столбца прибавить соответствующие
элементы другой строки или столбца,
умноженные на одно число.
Слайд 29С помощью свойства 6 добиваются
того, чтобы в некоторой строке
или в
некотором столбце все элементы,
кроме одного, были равны
нулю.Затем раскладывают определитель
по элементам этой строки или столбца.
Слайд 39Метод приведения к
треугольному виду
Метод приведения к треугольному
виду заключается в таком
преобразовании
данного определителя,когда все элементы его, лежащие над
(под) одной из его диагональю,
становятся равными нулю.