Множества

общим свойством.
Множества обозначают большими латинскими буквами A,B,C,D,…X,Y,Z.
Объекты, объединенные общим

свойством, называются элементами множества и обозначаются малыми латинскими буквами a,b,c,d,…x,y.z.

множеству A, запись a A означает, что элемент a

не принадлежит множеству A.
Множество, число элементов которого конечно, называется конечным, в противном случае – бесконечным. Если элементы бесконечного множества можно пронумеровать с помощью чисел натурального ряда, то оно называется счетным, в противном случае – несчетным так, множество четных чисел есть счетное множество, а множество действительных чисел – несчетное множество.

Количество элементов в конечном множестве A, называется мощность множества и

обозначается |A| . Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø. Универсальное множество – это множество всех элементов, которые могут встретиться в исследовании. Обозначается Ω.

множества В, то говорят, что множество А есть подмножество множества

В и обозначается это как А В. Если А В и В А, то множества А и В называются равносильными, что записывается в виде А=В. Любое множество А есть подмножество самого себя. Такое подмножество называют несобственным подмножеством. К числу несобственных подмножеств относят также пустое множество. Все прочие подмножества исходного множества А называются собственными подмножествами.

которая описывает способ получения элементов множества из уже полученных элементов

или других объектов ;
характеристическим предикатом Р(x), т.е. описанием характеристического свойства, которым должны обладать его элементы : М={ x | Р(x) }.

недостаточно – необходимо определить способы конструирования новых множеств из уже

имеющихся, т.е. определить операции над множествами.

множество М, состоящее из элементов, принадлежащих хотя бы к одному

из множеств А и В, т.е.
М= А U В ={m | m Є А или m Є В }

Пересечением А ∩ В двух множеств А и В является множество М, состоящее из элементов, принадлежащих как множеству А, так и множеству В, т.е.
М= А ∩ В ={m | m Є А и m Є В }

из элементов, принадлежащих множеству А и не принадлежащих множеству В,

т.е.
М= А \ В ={m | m Є А и m Є В }

Симметрической разностью А + В множеств А и В является множество М, содержащее все элементы из А, не принадлежащие В, а также все элементы из В, не принадлежащие А, т.е.
М=А+В={m|m Є А и m Є В } или ={m|m Є А и m Є В }

множество, состоящее из элементов универсального множества Ω, не принадлежащих М

,т.е.



Операцию дополнения обозначают символом .

множество, есть формула;
б) Если А и В - формулы, то

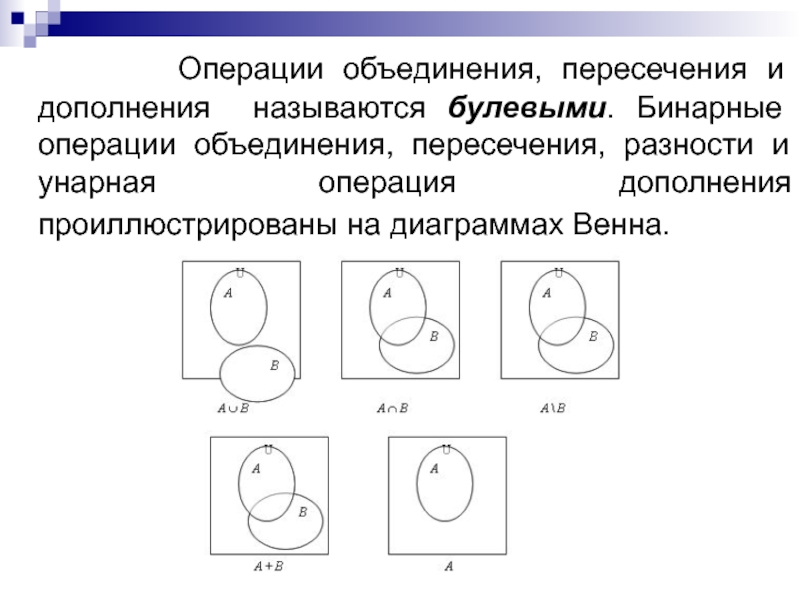
А U В, А ∩ В, А \ В, А+В, А – также есть формулы.

булевыми. Бинарные операции объединения, пересечения, разности и унарная операция дополнения

проиллюстрированы на диаграммах Венна.

подмножеств некоторого универсального множества с введенными выше операциями дополнения, пересечения

и объединения, составляют булеву алгебру множеств. Основные законы этой алгебры, используя общепринятое правило, что если в формуле отсутствуют скобки, устанавливающие порядок выполнения операций, то сначала выполняется дополнение, потом пересечение и затем объединение. Для повышения наглядности формулы знак пересечения множеств, подобно знаку арифметического умножения, будем опускать.

следующее: одна из формул получается из другой взаимной заменой всех

операций пересечения на операции объединения и всех символов ∅ на символы U. Этот факт известен под названием принципа двойственности.
Для операции пересечения пустое множество имеет свойство нуля, универсальное множество – свойство единицы. Для операции объединения универсальное множество имеет свойство нуля, а пустое множество – свойство единицы.

задания множества. Две формулы равносильны, если они представляют одно и

то же множество. Любую формулу булевой алгебры множеств можно вывести путем равносильных преобразований, используя формулы из приведенного списка. Данный список является достаточным, но для вывода любой формулы данной алгебры можно воспользоваться меньшим списком, т.е. некоторые формулы этого списка можно вывести из других.

образом.
Ее правую часть, используя дистрибутивность пересечения, представим как (А ∪ В) (А ∪ С) = (А ∪ В) А ∪ (А ∪ В) С.

Раскрыв скобки (по закону ассоциативности), получим (А ∪ В) А ∪ (А ∪ В) С =
= А А ∪ В А ∪ А С ∪ В С.

результате чего после применения закона коммутативности пересечения правая часть примет

вид
А Ω ∪ А В ∪ А С ∪ В С. После вынесения за скобки А получим А (Ω ∪ В ∪ С) ∪ В С, что равно левой части исходного выражения согласно свойству константы Ω.

списке:
А ∪ А В = А Ω  ∪ А В = А (Ω  ∪ В) = А.
Используя принцип двойственности, получим: А (А ∪ В) = А.

только что выведенную формулу и закон поглощения, докажем А ∪А В = А ∪ В:

А ∪А В = А Ω  ∪А В = АΩ  ∪А В ∪ U В = 
= А ∪А В ∪ В = А ∪ В.

как разбиение и покрытие.
Пусть ={Еi } i Є I –некоторое

подмножество множества М, Еi Є М. Семейство называется покрытием множества М, если каждый элемент М принадлежит хотя бы одному из Еi :

не пересекаются, т.е. каждый элемент множества М принадлежит не более

чем одному из множеств Еi :


Дизъюнктивное покрытие называется разбиением множества.

является покрытием, но не разбиением;
{{1}, {2}, {3}} является

разбиением и покрытием, а семейство {{1}, {2}} является дизъюнктивным, но не является ни покрытием, ни разбиением...