Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества
Содержание
- 1. Множества
- 2. МножестваМножество - совокупность (набор) некоторых объектов. Эти
- 3. Обозначения – выучить!!!
- 4. Числовая прямая. Числовые множества. Множество натуральных чисел:
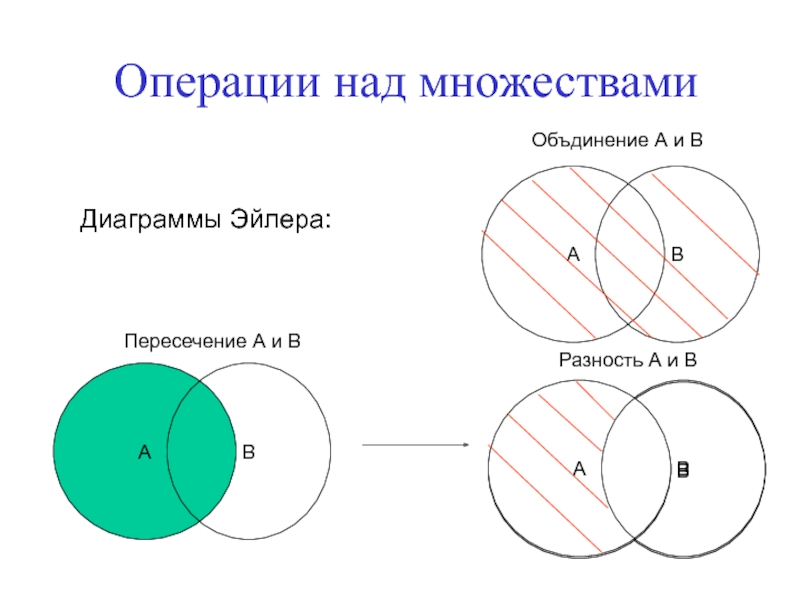
- 5. Операции над множествамиДиаграммы Эйлера:
- 6. УпражненияA={1,3,6,8}, B={2,4,6,8}. Найти – объединение и пересечение
- 7. Декартово произведение множествДекартовым (или прямым) произведением множества
- 8. Операции с комплексными числамиПравило сложения и вычитания
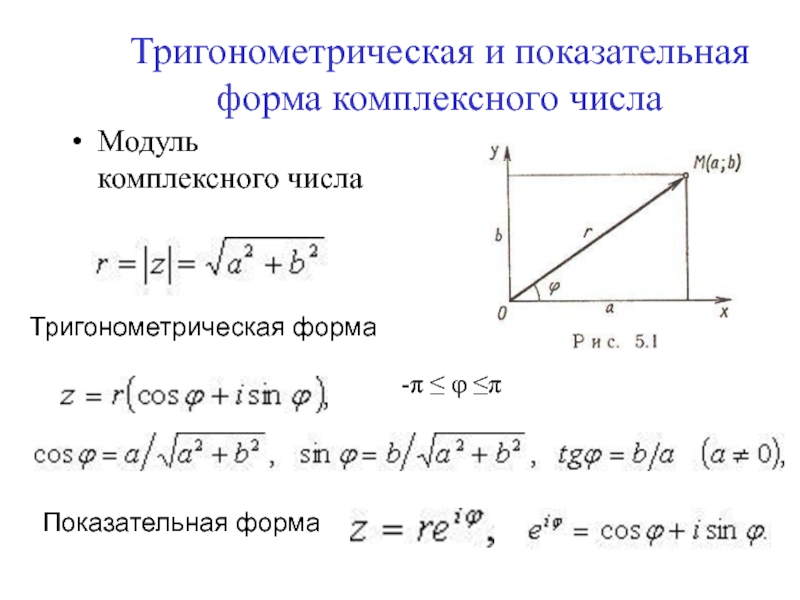
- 9. Тригонометрическая и показательная форма комплексного числаМодуль комплексного числа Тригонометрическая формаПоказательная форма-π ≤ φ ≤π
- 10. Действия с комплексными числамиФормула Муавра для возведения в натуральную степеньИзвлечение корня из комплексного числа
- 11. Упражнения на дом
- 12. Системы координатДекартоваПолярная
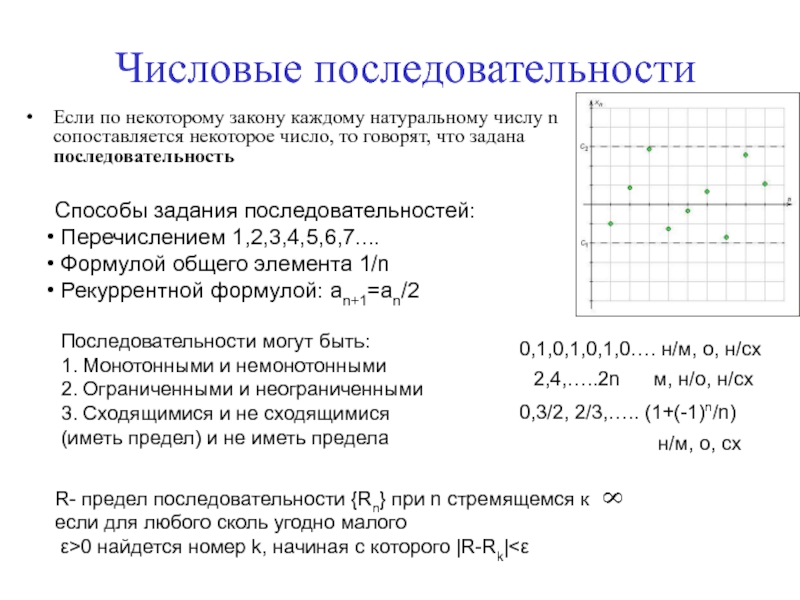
- 13. Числовые последовательностиЕсли по некоторому закону каждому натуральному
- 14. Любая неубывающая ограниченная сверху последовательность сходится.Любая невозрастающая
- 15. Некоторые приемы вычисления предела последовательности.Вынесение старшей степениИспользование замечательных пределовИспользование теорем и свойствНеопределенности: ; 1∞.
- 16. Функции одной переменнойЕсли каждому значению х числового
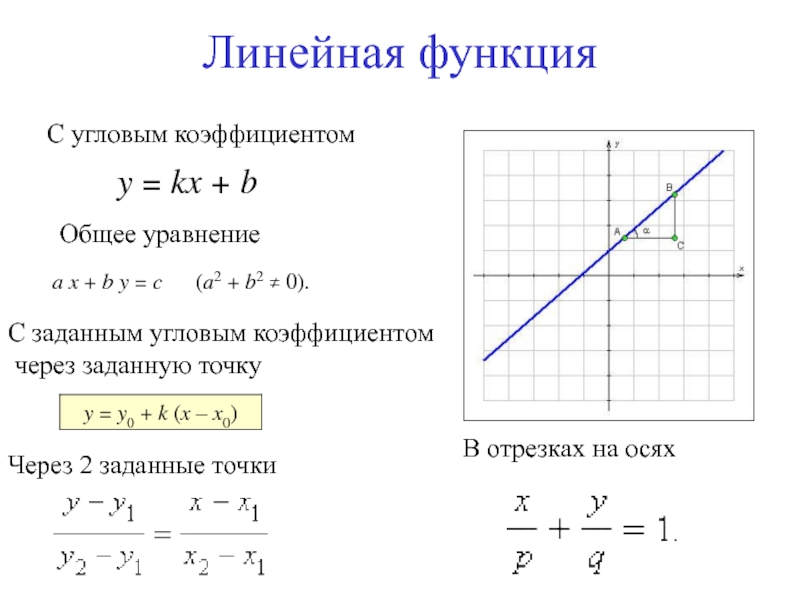
- 17. Линейная функцияС угловым коэффициентомОбщее уравнениеС заданным угловым
- 18. Предел функции в точке. Бесконечно малые и
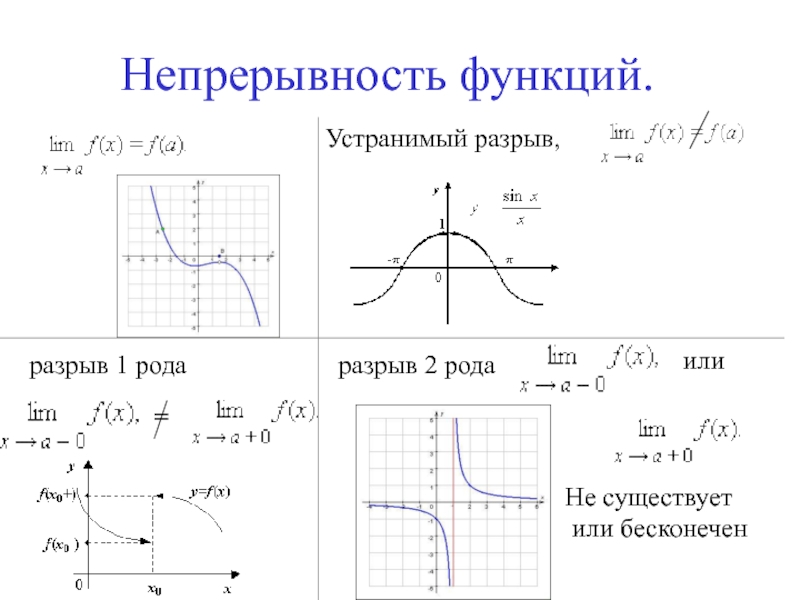
- 19. Непрерывность функций. Устранимый разрыв, разрыв 1 рода=разрыв 2 рода илиНе существует или бесконечен
- 20. Сложная функцияФункция от функции: f(x)=z(y(x))F(x)=(x+1)2, y(x)= x+1, z(y)=y2
- 21. функция спросаЗависимость спроса от различных факторов называется функцией
- 22. Полезность, бюджетная линия потребителяПолезность — это способность
- 23. Кривые безразличиякривые безразличия демонстрируют все возможные комбинации
- 24. Соотношение цены и потребления. Соотношение дохода и
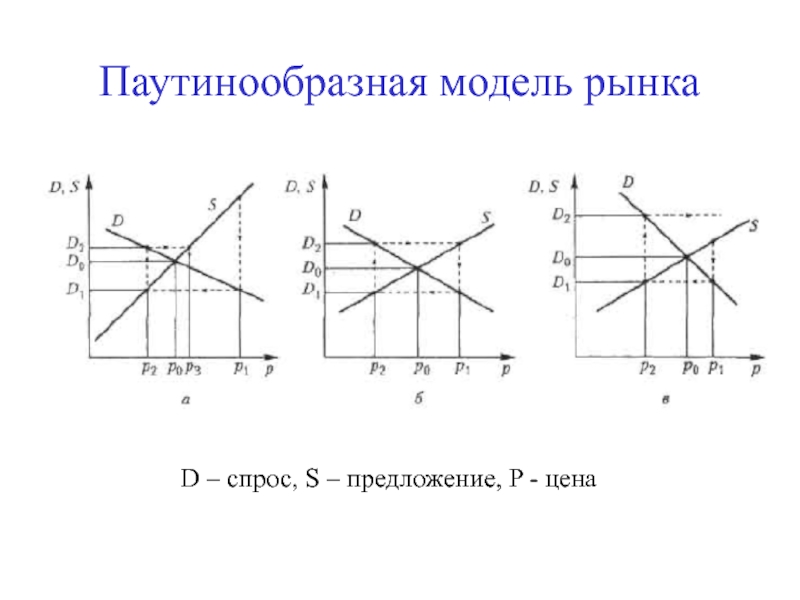
- 25. Паутинообразная модель рынка D – спрос, S – предложение, P - цена
- 26. Домашнее заданиеКрасс, Чупрынов – главы 3 и 4 Таблица производных – найти и выучить
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математика
1 семестр
встреча №1
Лектор: Шаталина Евгения Сергеевна
Литература: «Математика для
экономистов»,
Слайд 2Множества
Множество - совокупность (набор) некоторых объектов. Эти объекты - элементы
множества
Множество А является подмножеством множества B (A содержится в B),
если каждый элемент A есть элемент B Два множества называются равными, если они состоят из одних и тех же элементов.
"пустое множество" - множество, не содержащее ни одного элемента. Его обозначают
Слайд 4Числовая прямая. Числовые множества.
Множество натуральных чисел: N
температура
Множество целых чисел:
Z
Разрешимость линейных уравнений
Множество рациональных чисел: Q
Разрешимость квадратных уравнений
Множество вещественных (действительных)
чисел: RМодуль действительного числа:
N
Z
R
Q
Основные свойства модуля:
|x| = |-x|
|x+y|≤|x|+|y|
|x-y|≥|x|-|y|
Слайд 6Упражнения
A={1,3,6,8}, B={2,4,6,8}. Найти – объединение и пересечение этих множеств.
Чему равно
(A\B) U A ?
A= (5;7] U {10}, B = (4;8).
Найти пересечение этих множеств. Найти B\AСлайд 7Декартово произведение множеств
Декартовым (или прямым) произведением множества А на множество
В называется множество всех упорядоченных пар, в которых первая компонента
– элемент множества А, а вторая – элемент множества В.А×В={(x, y) |x∈A, y∈B}.
Точками показаны элементы
декартова произведения множеств А={1, 2, 3}
и В={4, 5, 6, 7}.
Способ нахождения общего числа элементов в декартовом произведении двух множеств:
если m(А)=n, m(B)=k, то m(А×В)=n⋅k
Слайд 8Операции с комплексными числами
Правило сложения и вычитания комплексных чисел
(a +
bi) + (c + di) = (a + c) +
(b + d)i.(a + bi) – (c + di) = (a – c) + (b – d)i.
Правило умножения
(a + bi)(c + di) = (aс - bd) + (ad + bc)i
Правило деления
(a + bi)/(c + di)=(ac+bd)/(c2+d2)+(bc-ad)i/(c2+d2)
По определению элемент i (мнимая единица) таков, что i2 = – 1
Слайд 9Тригонометрическая и показательная форма комплексного числа
Модуль комплексного числа
Тригонометрическая форма
Показательная
форма
-π ≤ φ ≤π
Слайд 10Действия с комплексными числами
Формула Муавра для возведения в натуральную степень
Извлечение
корня из комплексного числа
Слайд 13Числовые последовательности
Если по некоторому закону каждому натуральному числу n сопоставляется
некоторое число, то говорят, что задана последовательность
Последовательности могут быть:
1. Монотонными
и немонотонными 2. Ограниченными и неограниченными
3. Сходящимися и не сходящимися
(иметь предел) и не иметь предела
Способы задания последовательностей:
Перечислением 1,2,3,4,5,6,7....
Формулой общего элемента 1/n
Рекуррентной формулой: an+1=an/2
R- предел последовательности {Rn} при n стремящемся к
если для любого сколь угодно малого
ε>0 найдется номер k, начиная с которого |R-Rk|<ε
0,1,0,1,0,1,0…. н/м, о, н/сх
2,4,…..2n м, н/о, н/сх
0,3/2, 2/3,….. (1+(-1)n/n)
н/м, о, сх
8
Слайд 14Любая неубывающая ограниченная сверху последовательность сходится.
Любая невозрастающая ограниченная снизу последовательность
сходится.
Теорема «о двух милиционерах»
Основные свойства сходящихся последовательностей.
Бесконечно малые
и бесконечно большие при условии, что b ≠ 0 и для всех n.
Бесконечно малая
Бесконечно большая
Если последовательности {xn}, {yn}, {zn} таковы, что xn ≤ yn ≤ zn для всех n ≥ N, и
то последовательность {yn} сходится, и
Слайд 15Некоторые приемы вычисления предела последовательности.
Вынесение старшей степени
Использование замечательных пределов
Использование теорем
и свойств
Неопределенности:
; 1∞.
Слайд 16Функции одной переменной
Если каждому значению х числового множества X по
правилу f соответствует единственное число множества Y, то говорят, что
на числовом множестве X задана функция у = f(x), x X. В этом случае х называется аргументом, у - значением функции. Множество X называется областью определения функции, Y - множеством значений функции.Способы задания функции:
Табличный
Графический
Аналитический
Словесный
Графиком функции у = f(x) называется множество точек плоскости, координаты х, у которых удовлетворяют соотношению у = f(x).
Область определения и область значений функции
Монотонность и ограниченность функции
Периодические функции
Слайд 17Линейная функция
С угловым коэффициентом
Общее уравнение
С заданным угловым коэффициентом
через заданную
точку
Через 2 заданные точки
В отрезках на осях
Слайд 18Предел функции в точке. Бесконечно малые и бесконечно большие функции.
Замечательные пределы.
⇔
Левый
и правый пределы функцииСлайд 19Непрерывность функций.
Устранимый разрыв,
разрыв 1 рода
=
разрыв 2 рода
или
Не
существует
или бесконечен
Слайд 21функция спроса
Зависимость спроса от различных факторов называется функцией спроса
В наиболее простом
случае функцию спроса выражают исключительно от цены на товар, как
от основного фактора, влияющего на спросa – максимально возможный спрос на рынке на данный товар,
b – зависимость изменения спроса от изменения цены (одновременно отражает и угол наклона кривой спроса),
p – цена на товар.
d- объем спроса
Знак «минус» показывает, что функция спроса имеет убывающий вид.
Слайд 22Полезность, бюджетная линия потребителя
Полезность — это способность продукта удовлетворять потребителя.
Полезность определенного продукта будет существенно различной для разных людей.
Слайд 23Кривые безразличия
кривые безразличия демонстрируют все возможные
комбинации продуктов A и
B, дающие потребителю
равный объем удовлетворения потребности, или полезности.
Слайд 24Соотношение цены и потребления. Соотношение дохода и потребления.
потребитель выберет такую
точку на бюджетной линии, которая поставит его на наиболее высокую
изо всех доступных ему кривую безразличия;изменение цены одного из продуктов приводит к смещению бюджетной линии и выявлению нового положения равновесия.
изменение дохода потребителя приводит к смещению бюджетной линии и выявлению нового положения равновесия.




![Множества УпражненияA={1,3,6,8}, B={2,4,6,8}. Найти – объединение и пересечение этих множеств.Чему равно (A\B) УпражненияA={1,3,6,8}, B={2,4,6,8}. Найти – объединение и пересечение этих множеств.Чему равно (A\B) U A ?A= (5;7] U {10},](/img/thumbs/5fc16a5b07aa1c666adeff6a2faa429a-800x.jpg)