Слайд 1Элементы математической логики
Логика в информатике и искусственном интеллекте.
Алгебра логики (алгебра
высказываний) — раздел математической логики, в котором изучаются логические операции
над высказываниями. Предполагается, что высказывания могут быть только истинными или ложными (т.н. бинарная или двоичная логика, в отличие от, например, троичной логики, когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено»).
Логика высказываний – основной математический инструмент при создании компьютеров, легко преобразуется в битовую: (0 — ЛОЖЬ, 1 — ИСТИНА);
Слайд 2
Историческая справка
Начало исследований в области формальной логики было положено греческим
философом Аристотелем, 384-322 гг. до н.э. Он основоположник формальной логики.
Впервые перевести логику на язык математики предложил немецкий математик Г. Лейбниц в конце ХVII века. Эту идею впервые реализовал англ.
математик Дж. Буль (1815 – 1864г.).
Буль создал алгебру, в которой буквами м
обозначены высказывания, и это привело
к алгебре высказываний.
Алгебра логики находит непосредственное и широкое применение при разработке средств электронной и вычислительной техники.
Слайд 3Определения
Высказывание – это повествовательное предложение, которому можно поставить в соответствие
одно из двух значений – истина или ложь. Высказывания строятся
над множеством {B,¬, ∧, ∨, 0, 1}, где B — непустое множество, над элементами которого определены три операции: ¬ - отрицание (унарная операция), ∧ - конъюнкция (бинарная), ∨ - дизъюнкция (бинарная),
а также константы — логический ноль 0 и логическая единица 1.
B = {Ложь, Истина}. Для B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Слайд 4Отрицание
A
0
1
1
0
A
0
1
1
0
Отрицанием высказывания А называется новое высказывание, которое является истинным, если
высказывание А ложно, и ложным, если высказывание А истинно. Обозначается
отрицание или ¬ А и читается “не А” или “неверно, что А”. Логические значения высказываний можно описать с помощью таблицы истинности, где 0 означает ложь, а 1 – истину. Таблица истинности для отрицания имеет вид:
Двойное отрицание высказывания А совпадает с самим высказыванием А.
Слайд 5Конъюнкция
A
0
1
1
0
A
0
1
1
0
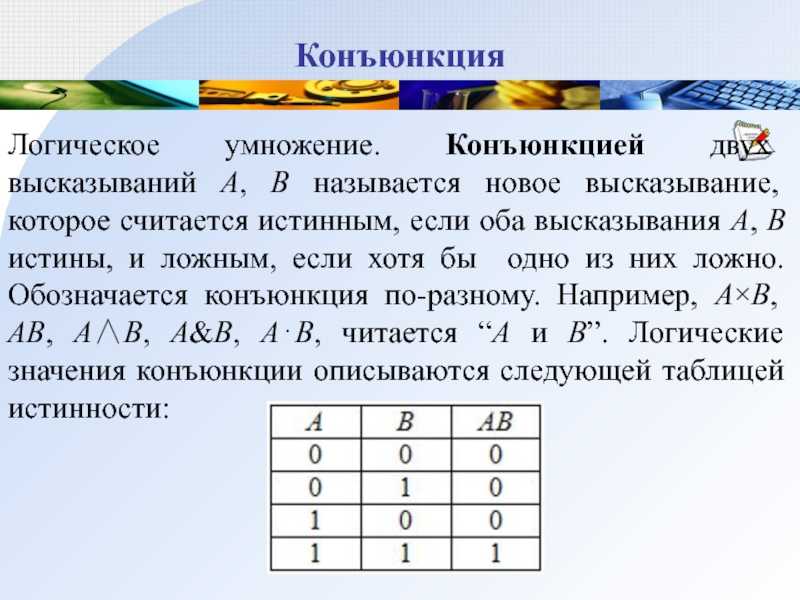
Логическое умножение. Конъюнкцией двух высказываний А, В называется новое высказывание,
которое считается истинным, если оба высказывания А, В истины, и
ложным, если хотя бы одно из них ложно. Обозначается конъюнкция по-разному. Например, А×B, AB, А∧В, А&B, А⋅B, читается “А и В”. Логические значения конъюнкции описываются следующей таблицей истинности:
Слайд 6Дизъюнкция
A
0
1
1
0
A
0
1
1
0
Логическое сложение. Дизъюнкцией двух высказываний A, B называется новое высказывание,
которое считается истинным, если хотя бы одно из высказываний истинно,
и ложным, если они оба ложны. Дизъюнкция высказываний A, B обозначается символом А ∨ В, (А + В) читается «A или B». Высказывания A, B при этом называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:
Слайд 7Импликация
A
0
1
1
0
A
0
1
1
0
A
B
A→B
0
0
1
0
1
1
1
0
0
1
1
1
Импликацией двух высказываний A, B называется новое высказывание, которое считается
ложным, если A истинно, а B - ложно, и истинным
во всех остальных случаях. Обозначается символом A→B, читается «Если A, то B» или «из A следует B». При этом высказывание A называется условием или посылкой, высказывание В – следствием или заключением, высказывание А→В следованием или импликацией.
Таблица истинности:
A
B
A→B
0
0
1
0
1
1
1
0
0
1
1
1
Слайд 8Эквиваленция
A
0
1
1
0
A
0
1
1
0
A
B
A→B
0
0
1
0
1
1
1
0
0
1
1
1
Эквиваленцией (или эквивалентностью) двух высказываний А, В называется новое высказывание,
которое считается истинным, когда оба высказывания А, В либо одновременно
истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний А, В обозначается символом А↔В, читается «для того, чтобы В, необходимо и достаточно, чтобы А», или «А тогда и только тогда, когда В».
Таблица истинности
A
B
A→B
0
0
1
0
1
1
1
0
0
1
1
1
Слайд 9 Формулы алгебры логики
Приоритеты при выполнении операций алгебры логики:
Выполнение операций
в скобках
Операция логического отрицания
Операция логического умножения
Операция логического сложения
Операция импликации
Операция эквивалентности
Операции
с равным приоритетом выполняются слева направо.
Слайд 10
Пример. Высказывание «Треугольник АВС с вершиной в точке С и
основанием АВ равнобедренный тогда и только тогда, когда ∠A =
∠B » является истинным, так как высказывания «Треугольник АВС с вершиной в точке С и основанием АВ равнобедренный» и «В равнобедренном треугольнике АВС с вершиной в точке С и основанием АВ ∠A = ∠B» либо одновременно истинны, либо одновременно ложны.
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем математики формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух элементов эквивалентности и доказав истинности самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
Слайд 11
Пример. Пусть А - высказывание «Вася изучает программирование», В -
высказывание «Вася любит математику». Рассмотрим словесную формулировку высказываний: 1) А∨В;
2) ; 3) A → B;
4) 5) 6)
Решение:
1) «Вася изучает программирование или любит математику».
2) «Вася не изучает программирование и не любит математику».
3) «Если Вася изучает программирование, то он любит математику».
4) «Неверно, что если Вася изучает программирование, то он любит математику».
Слайд 12
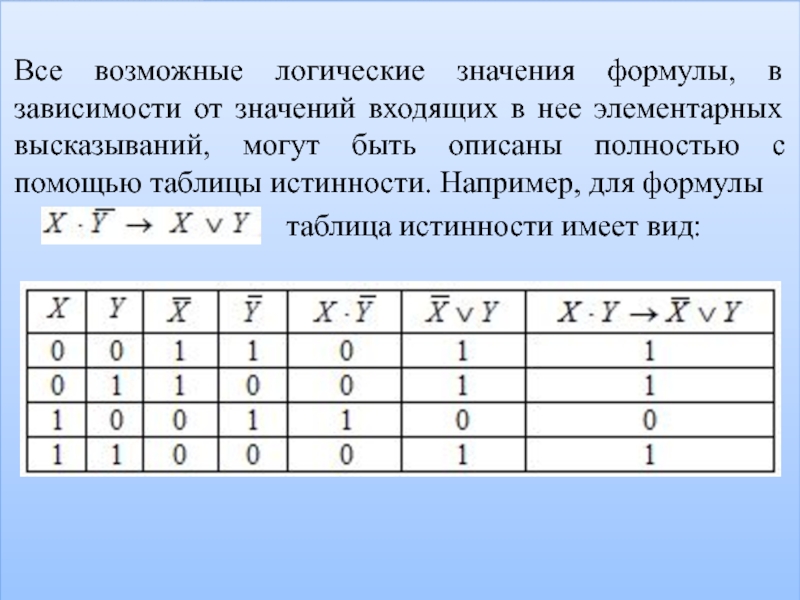
Все возможные логические значения формулы, в зависимости от значений входящих
в нее элементарных высказываний, могут быть описаны полностью с помощью
таблицы истинности. Например, для формулы
таблица истинности имеет вид:
Слайд 13
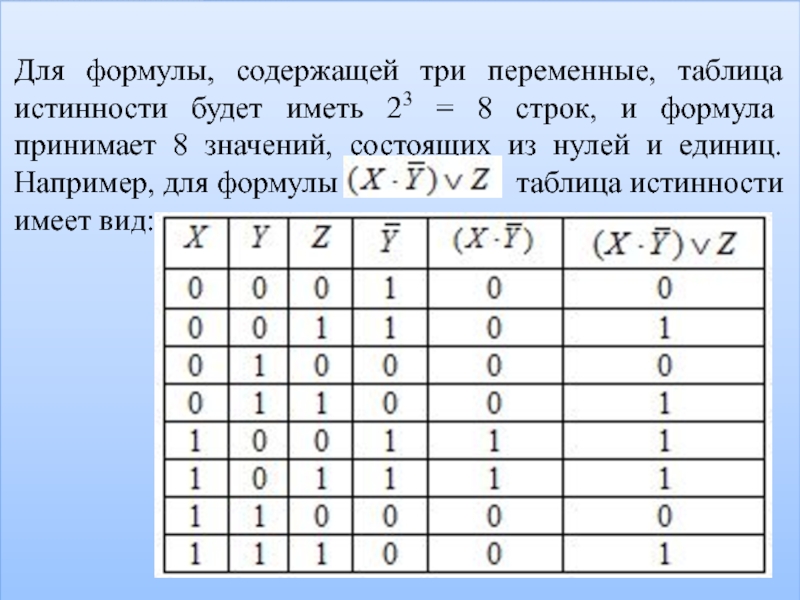
Для формулы, содержащей три переменные, таблица истинности будет иметь 23
= 8 строк, и формула принимает 8 значений, состоящих из
нулей и единиц. Например, для формулы таблица истинности имеет вид:
Слайд 14Равносильные формулы алгебры логики
Две формулы алгебры логики А и В
называются равносильными, если они принимают одинаковые логические значения на любом
наборе значений элементарных высказываний, входящих в формулу. Запись A=B означает, что формулы А и В равносильны. Например, очевидно, что равносильны формулы:
Х=X; Х&Х=X; Х&0 =0; Х∨1=1; Х∨ =1; X∨Х=X; X&1=X; X∨0=X; X& =0.
Легко видеть, что если А = В, то .
Слайд 15 Тавтология
Формула А называется тождественно истинной (или тавтологией), если она
принимает значение 1 при всех значениях входящих в нее переменных.
Например, тождественно истинной является формула X→(Y→X), что можно проверить, построив таблицу истинности.
Формула называется тождественно ложной, если она принимает значение ноль при всех значениях входящих в нее переменных. Как уже отмечалось , то есть формула тождественно ложная.
Слайд 16 Свойства отношений равносильности
А=А (рефлексивно);
Если A=В, то B=A (симметрично);
Если
А=В и B=С, то A=С (транзитивно).
Между понятиями равносильности и эквивалентности
существует следующая связь: если формулы А и В равносильны, то формула А↔В тавтология (то есть тождественно истинная), и, обратно, если формула А↔В тавтология, то формулы А и В равносильны.
Слайд 17
Равносильности, выражающие одни логические операции через другие
Всякую формулу алгебры логики
можно заменить равносильной ей формулой, содержащей только две логических операции:
конъюнкцию и отрицание или дизъюнкцию и отрицание.
Слайд 18Штрих Шеффера
Очевидно, что имеют место равносильности: =X|X, X⋅Y=(X|Y)|(X|Y). Из
этих двух равносильностей следует, что всякая формула алгебры логики может
быть заменена равносильной формулой, содержащей только операцию «штрих Шеффера». Отметим, что X|Y = . Аналогично операции «штрих Шеффера» может быть использована операция, называемая «стрелкой Пирса»:
Слайд 19Равносильности, выражающие основные законы алгебры логики
Слайд 20
Между равносильностями, записанными в дизъюнктивной форме и в конъюнктивной форме,
существует свойство симметрии: если дизъюнкцию заменить конъюнкцией, а конъюнкцию заменить
дизъюнкцией, 0 заменить на 1, а 1 заменить на 0, при этом отрицания сохранить без изменений, то записанные слева и справа равносильности перейдут друг в друга. Следовательно, с помощью указанных замен можно из одних равносильностей получить другие. Это называется законом двойственности.
Закон двойственности
Слайд 21
Многие законы можно обобщить на случай большого числа переменных
A∨B⋅C⋅D⋅…⋅P =
(A∨B)⋅(A∨C)⋅(A∨D)⋅ … ⋅(A∨P) и A⋅(B∨C∨D∨…∨P) = A⋅B∨A⋅C∨A⋅D∨…∨A⋅P
А∨
A⋅B ∨ A⋅B⋅С⋅D = A;
A⋅(A∨C∨D∨…∨P) = A;
Слайд 23Нормальные формы логических выражений
Совершенная дизъюнктивно нормальная форма (СДНФ): ДНФ, удовлетворяющая
условиям:
Все элементарные конъюнкции различны;
Нет нулевых конъюнкций;
Ни одна из элементарных конъюнкций
не повторяется;
Каждая элементарная конъюнкция содержит все переменные или их отрицания.
Аналогичны условия для СКНФ.
СДНФ и СКНФ используются при проектировании элементов и узлов компьютера
Слайд 24
СДНФ. Для всех наборов переменных, на которых функция принимает единичные
значения, записываются конъюнкции этих переменных, инвертируя те переменные, которым соответствуют
нулевые значения. Затем конъюнкции соединяют знаком дизъюнкции.
СКНФ. Для всех наборов переменных, на которых функция принимает нулевые значения, записываются конъюнкции этих переменных, инвертируя те переменные, которым соответствуют единичные значения. Затем дизъюнкции соединяют знаком конъюнкции.
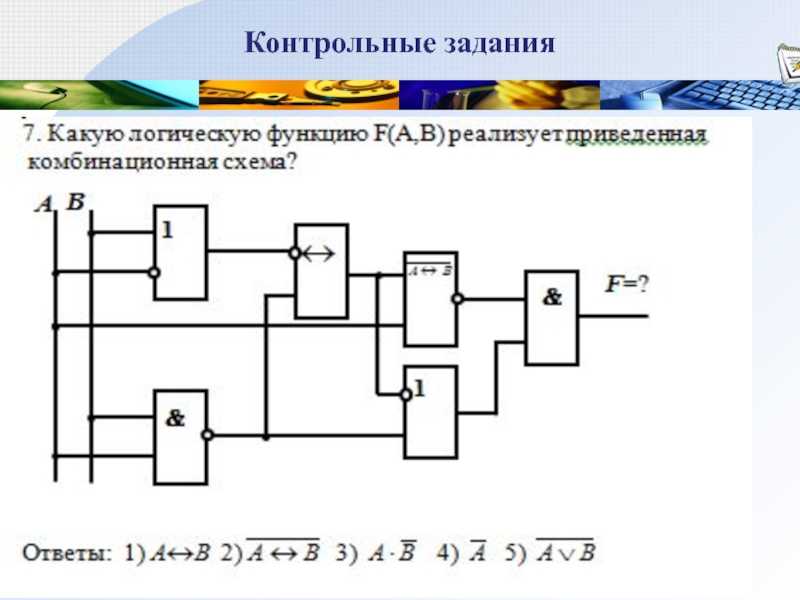
Слайд 28Контрольные задания
1. Представить в МДНФ:
2. Даны три числа в различных
системах счисления: A=16(10), B=21(8), C=12(10). Выполните следующие логические операции: AB+C.
Ответ напишите в шестнадцатеричной системе счисления и в десятичной системе.
3. Постройте таблицу истинности для логической функции
.
4. Построить логическую функцию по заданной таблице истинности, которая имеет нулевые значения при следующих наборах переменных A, B, C: (001), (010), (011), (110).
Слайд 29Постановка и методы решения задачи
минимизации ФАЛ
На основе ФАЛ осуществляется
построение схем различных АЛУ. Поэтому актуальной задачей является преобразование ФАЛ
к виду, обеспечивающему наиболее простую по количеству используемых логических элементов, схемную реализацию последовательного перебора.
В инженерной практике используются следующие основные методы минимизации: последовательного перебора, последовательного упрощения аналитического выражения, карт Карно(предусматривает задание ФАЛ в виде координатных карт состояний), Квайна, Квайна–Мак-Класки, Л.Т. Мавренкова и т. д.
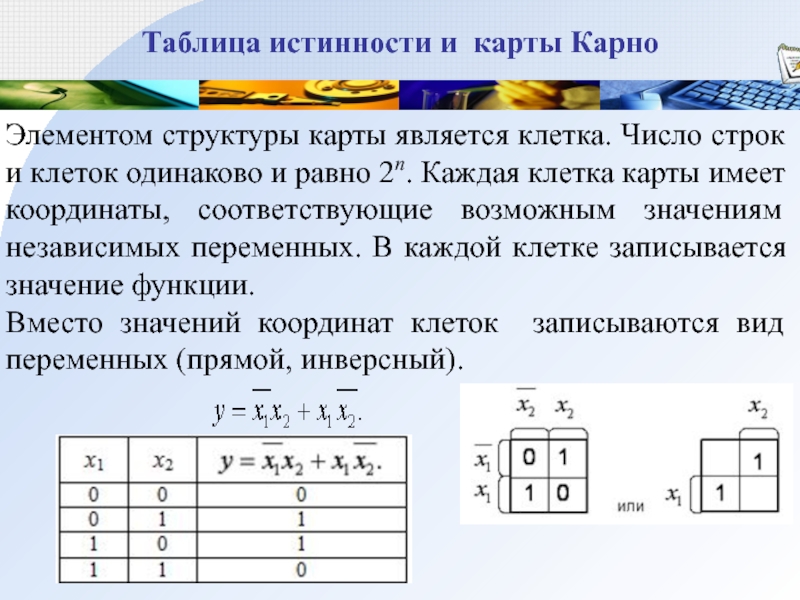
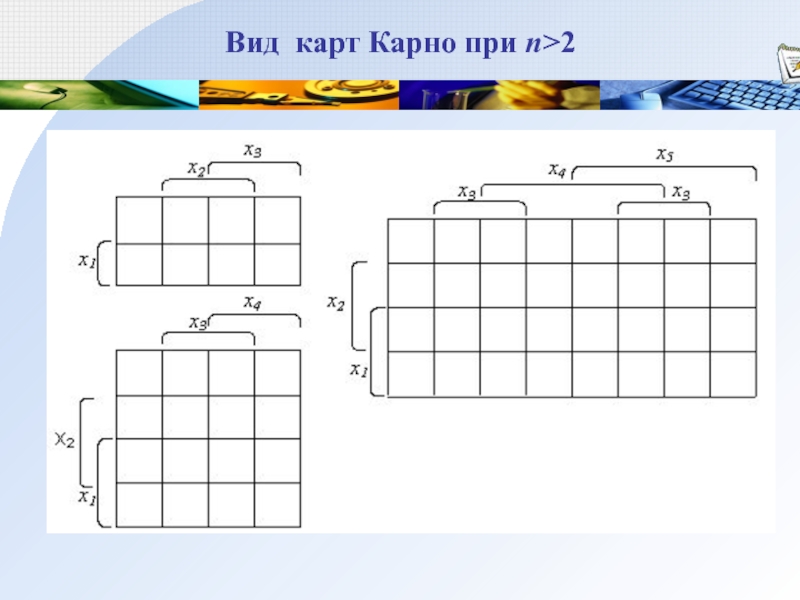
Слайд 30Таблица истинности и карты Карно
Элементом структуры карты является клетка. Число
строк и клеток одинаково и равно 2n. Каждая клетка карты имеет
координаты, соответствующие возможным значениям независимых переменных. В каждой клетке записывается значение функции.
Вместо значений координат клеток записываются вид переменных (прямой, инверсный).
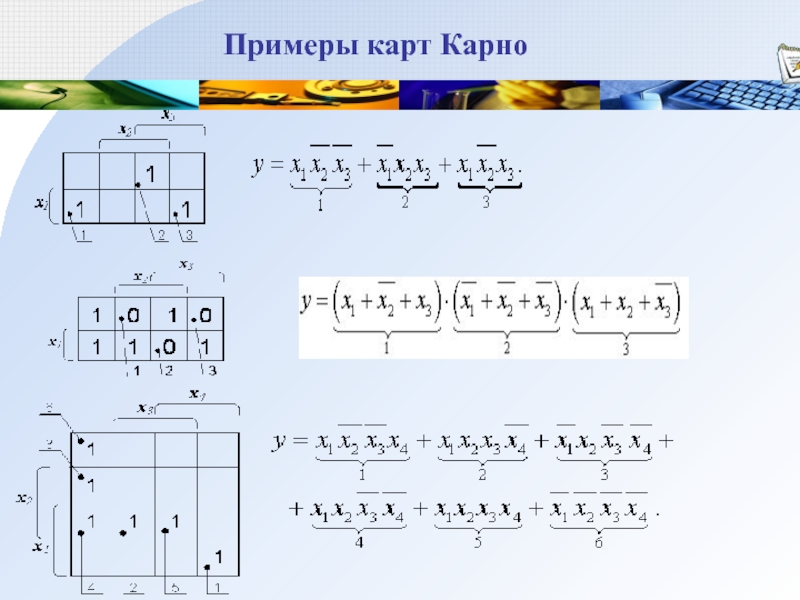
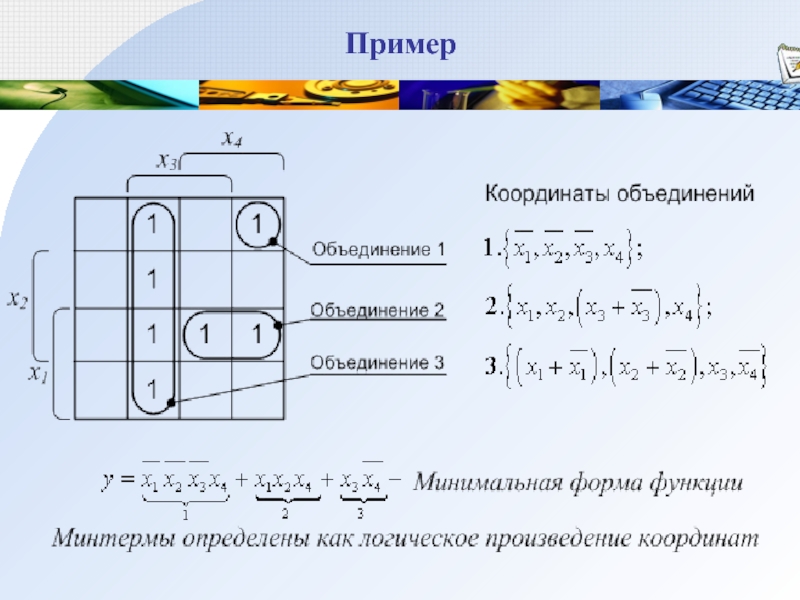
Слайд 33Минимизация с использованием карт Карно
Минимизации логических функций является графическим аналогом
операции склеивания, реализуемый с помощью карты Карно.
Склеиваются только соседние минтермы*,
а объединяются только соответствующие им единицы, которые всегда оказываются рядом стоящими.
* минтерм есть логическое произведение независимых переменных
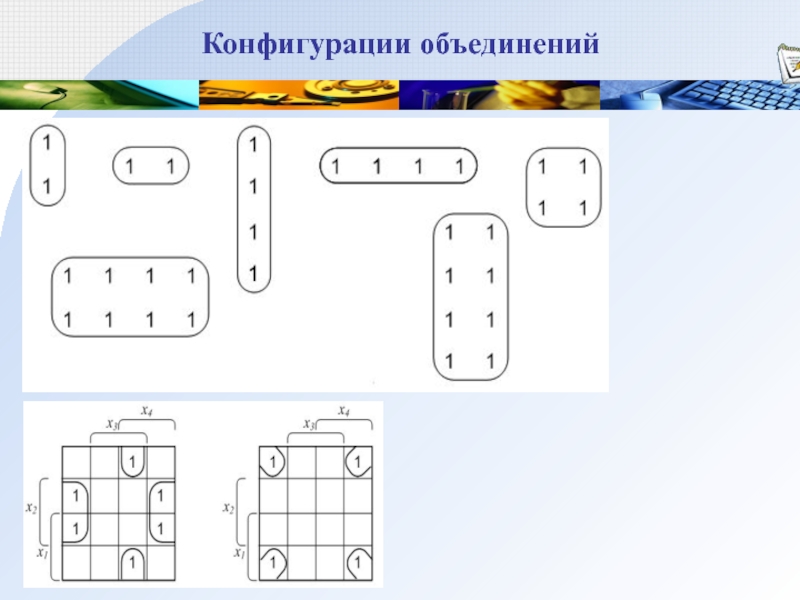
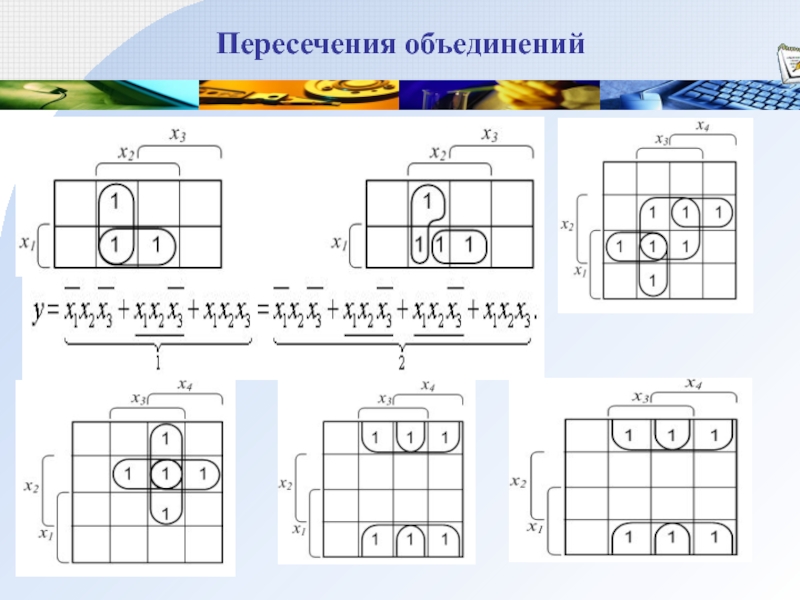
Слайд 36Пересечения объединений
Для достижения минимальной тупиковой формы функции необходимо обеспечить:
минимум числа
объединений единиц,
максимум единиц составляющих каждое объединение.
каждая единица на карте Карно
должна принадлежать какому-либо объединению, даже если объединение содержит только одну единицу,
объединение должно содержать хотя бы одну «свою» единицу, не принадлежащую ни к какому другому объединению.
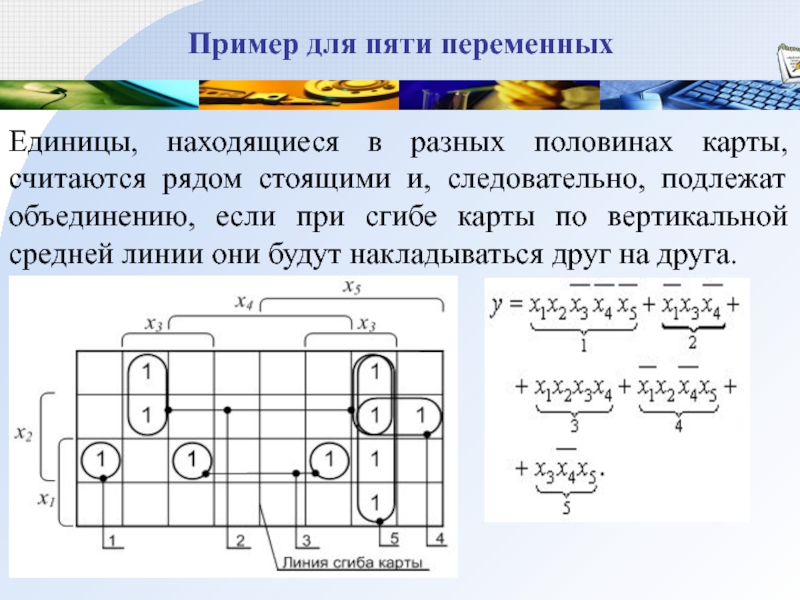
Слайд 38Пример для пяти переменных
Единицы, находящиеся в разных половинах карты, считаются
рядом стоящими и, следовательно, подлежат объединению, если при сгибе карты
по вертикальной средней линии они будут накладываться друг на друга.
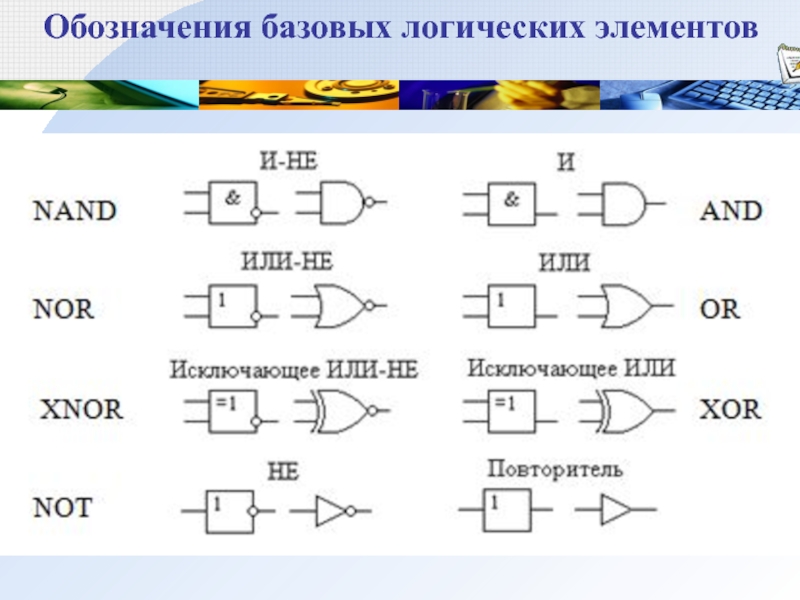
Слайд 40Основные логические и запоминающие элементы компьютера
В основе аппаратного обеспечения компьютеров
лежат так называемые вентили. Они представляют собой достаточно простые элементы,
которые можно комбинировать между собой. Под комбинационным цифровым устройством (КЦУ) понимается цифровое устройство, обеспечивающее преобразование совокупно-сти N входных цифровых сигналов в M выходных, при этом состояние выходных сигналов в данный момент времени определяется состоянием входных сигналов в этот же момент времени. КЦУ «не помнит» предыстории поступления сигналов на его входы. Правила функционирования КЦУ определяются реализуемыми ими функциями алгебры логики.
Слайд 41Обозначения базовых логических элементов
Слайд 42Обозначения базовых логических элементов
Вентиль - это устройство, которое выдает результат
булевой операции от введенных в него данных (сигналов).
Простейший вентиль представляет
собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот. Т.е. получаем вентиль НЕ.
Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕ и И-НЕ.
Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах).
Слайд 43Принцип построения
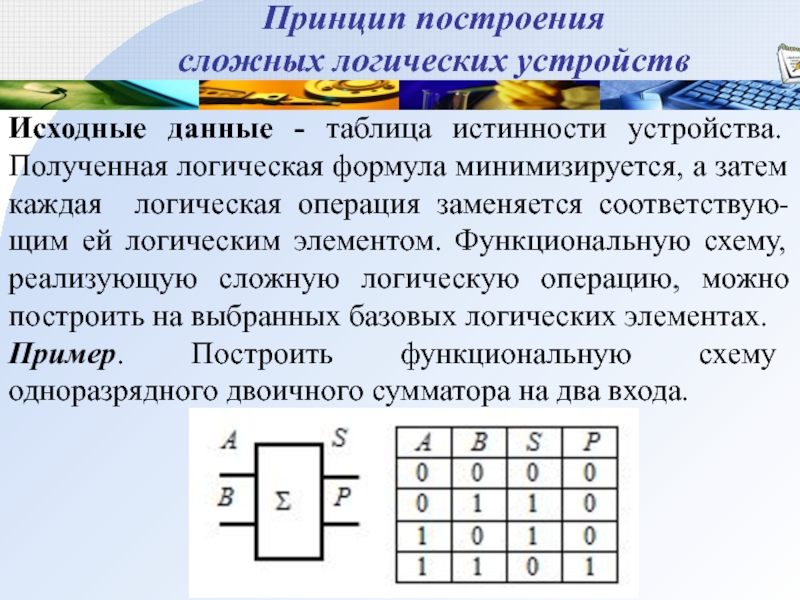
сложных логических устройств
Исходные данные - таблица истинности устройства. Полученная
логическая формула минимизируется, а затем каждая логическая операция заменяется соответствую-щим
ей логическим элементом. Функциональную схему, реализующую сложную логическую операцию, можно построить на выбранных базовых логических элементах.
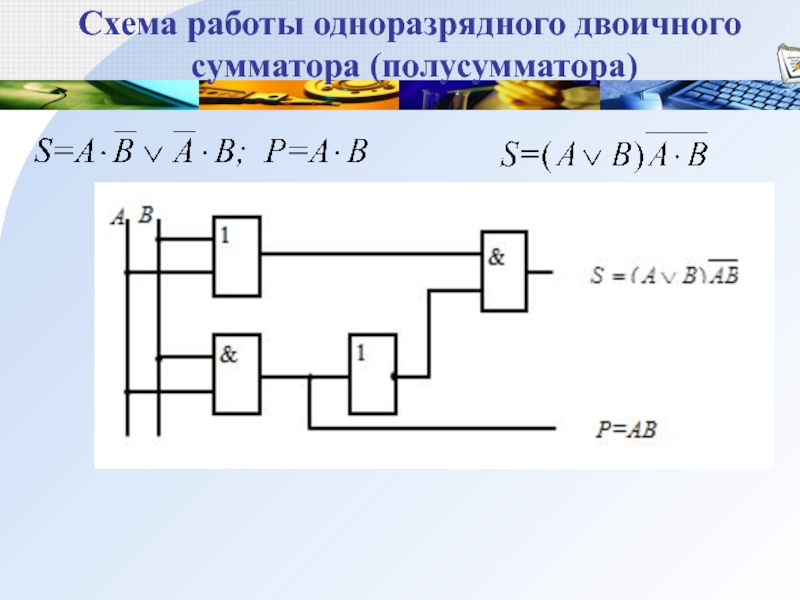
Пример. Построить функциональную схему одноразрядного двоичного сумматора на два входа.
Слайд 44Схема работы одноразрядного двоичного
сумматора (полусумматора)
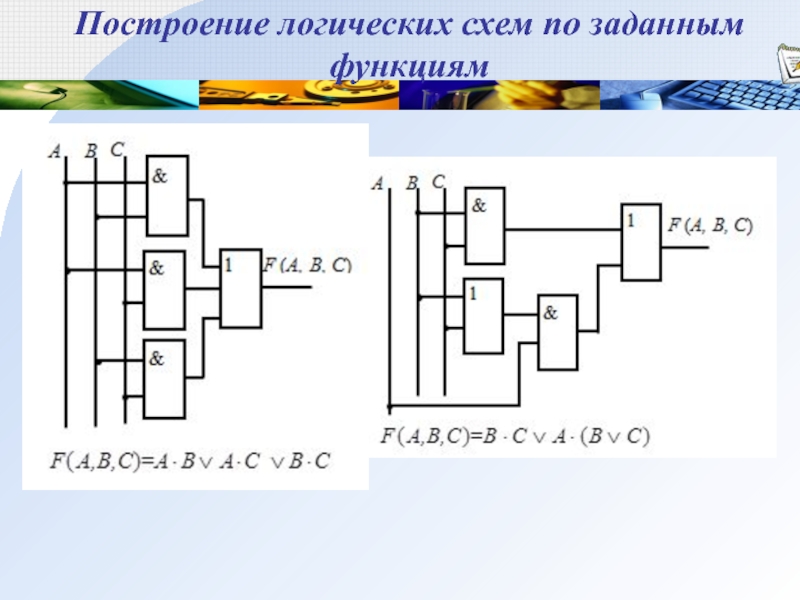
Слайд 45Построение логических схем по заданным функциям
Если на входах единичных сигналов
больше, чем нулевых, то функция F(A, В, С)=1, в остальных
случаях F(A, В, С)=0.
Слайд 46Построение логических схем по заданным функциям
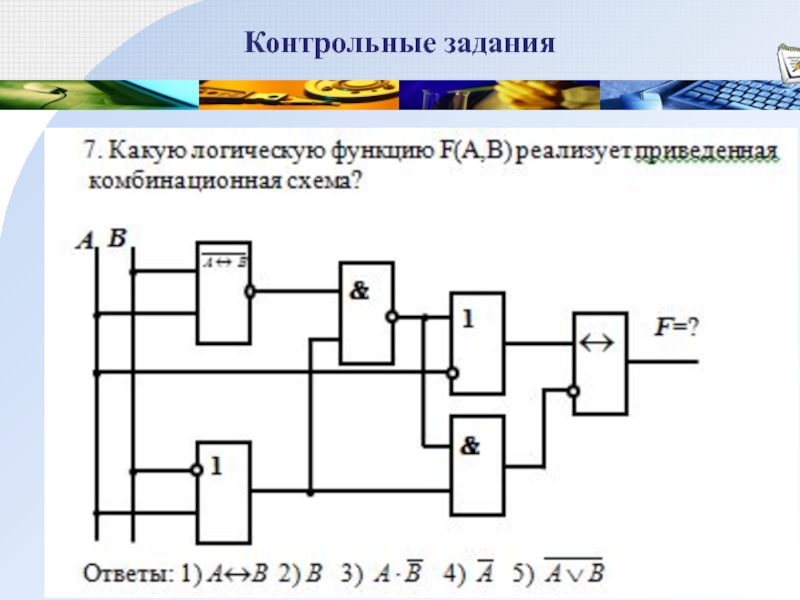
Слайд 47Контрольные задания
В компьютере имеется логический узел Y с тремя входами
А, В, С и одним выходом F(A,B,C). Логика работы узла
Y следующая: если хотя бы на двух любых входах сигналы разные, то функция F(A,B,C) = 1. В остальных случаях F(A,B,C) = 0. Построить логи-ческую схему узла Y на базе элементов И, ИЛИ, НЕ.