x, надо определить такое значение x*, при котором функция f(x)
принимает экстремальное значение. Под ним обычно понимают минимальное или максимальное значения. В общем случае функция может иметь одну или несколько экстремальных точек. Нахождение этих точек с заданной точностью можно разбить на два этапа. Сначала экстремальные точки отделяют, т.е. определяются отрезки, которые содержат по одной экстремальной точке, а затем уточняют до требуемой точности ε. Отделение можно осуществить, как графически, так и табулированием. Все методы уточнения точек экстремумов будем рассматривать относительно уточнения минимума на заданном отрезке.пример: f(x) = 3*sin(2*x)-1.5*x-1
f=inline(‘3*sin(2*x)-1.5*x-1');
x=-2:0.05:2;
plot(x,f(x))
grid on
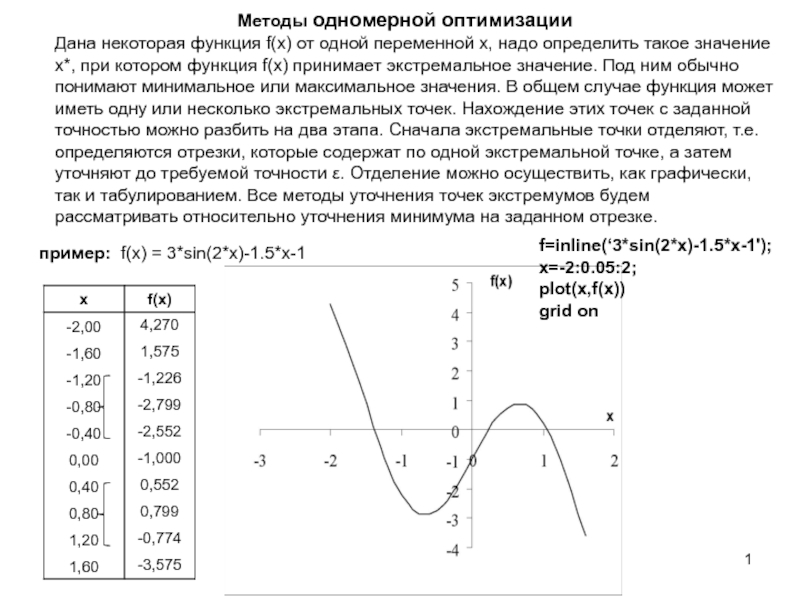
![Методы одномерной оптимизации Метод деления на три равных отрезка.Дан отрезок [a;b] на котором определена Метод деления на три равных отрезка.Дан отрезок [a;b] на котором определена функция f(x) и точность ε. Надо](/img/thumbs/01d6d02b1a1a3341a85408d376f79855-800x.jpg)

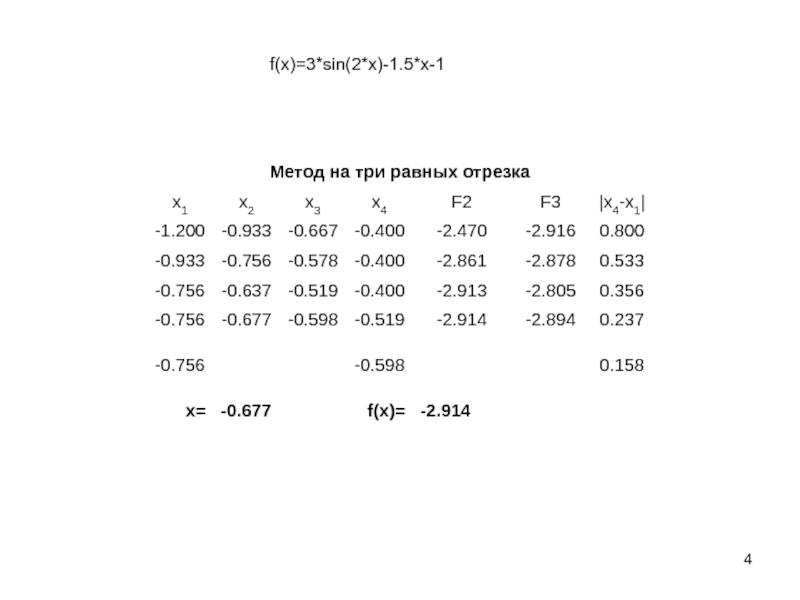
![Методы одномерной оптимизации Попробуем увеличить долю сокращения отрезкаДан отрезок [a;b] на котором определена функция Попробуем увеличить долю сокращения отрезкаДан отрезок [a;b] на котором определена функция f(x) и точность ε. Надо уточнить](/img/tmb/2/147213/e0cd3a7603635afc2f985b225f36bff8-800x.jpg)
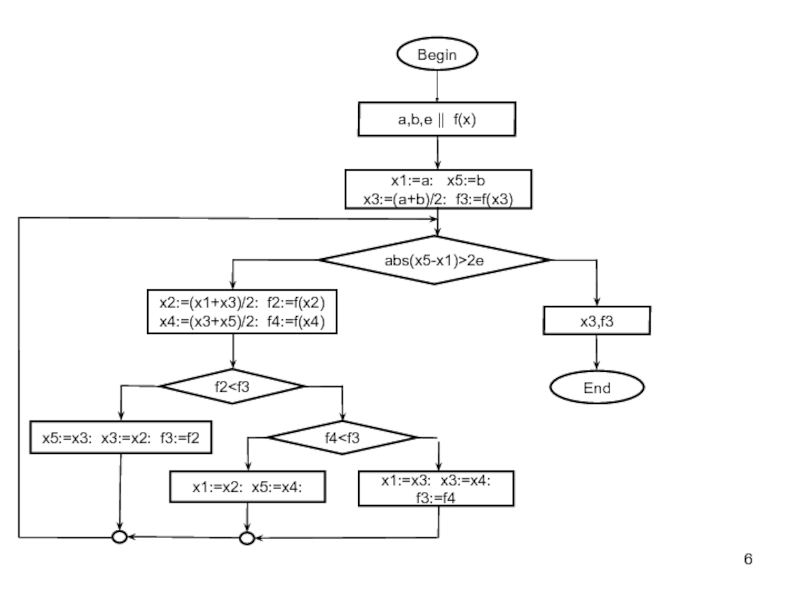
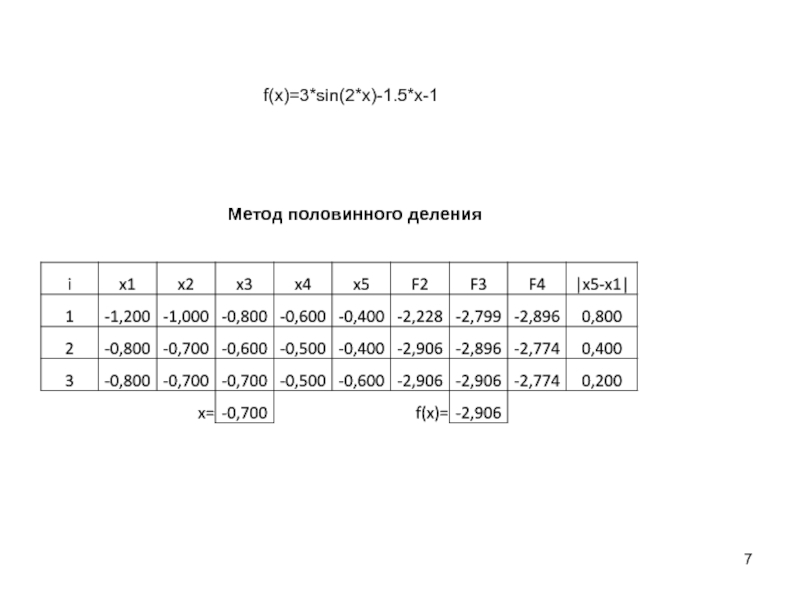

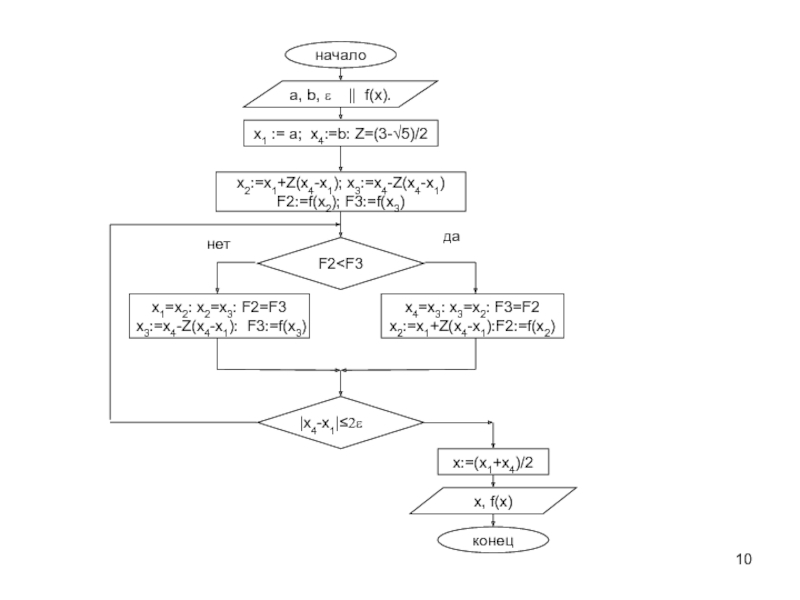
![Методы одномерной оптимизации Метод Золотого сечения.Дан отрезок [a;b] на котором определена функция f(x) и Метод Золотого сечения.Дан отрезок [a;b] на котором определена функция f(x) и точность ε. Надо уточнить точку минимума](/img/thumbs/2454ffc596ac944084c3b71beb2975f1-800x.jpg)
![Методы одномерной оптимизации f=inline(‘3*sin(2*x)-1.5*x-1');[x,y]=fminbnd(f,1.2,-0.4) f=inline(‘3*sin(2*x)-1.5*x-1');[x,y]=fminbnd(f,1.2,-0.4)](/img/thumbs/e5b9b17f6a9ab24f4485e139d3b80bb7-800x.jpg)
![Методы одномерной оптимизации Метод с обраным переменным шагом.Дан отрезок [a;b] на котором определена функция Метод с обраным переменным шагом.Дан отрезок [a;b] на котором определена функция f(x) и точность ε. Надо уточнить](/img/tmb/2/147213/4f2e595b8b266cca2aac032b89ec711b-800x.jpg)



















