Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории графов
Содержание
- 1. Элементы теории графов
- 2. ВехиГрафы Эйлера (1736)Теория Кирхгоф (1847)Деревья Кэли (1857) — задача о химических изомерахЦиклы Гамильтона (1859)
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Red, blue, or green: departmentsYellow: consultantsGrey: external expertsStructure of an organizationwww.orgnet.com
- 9. Topology of the protein networkH. Jeong, S.P.
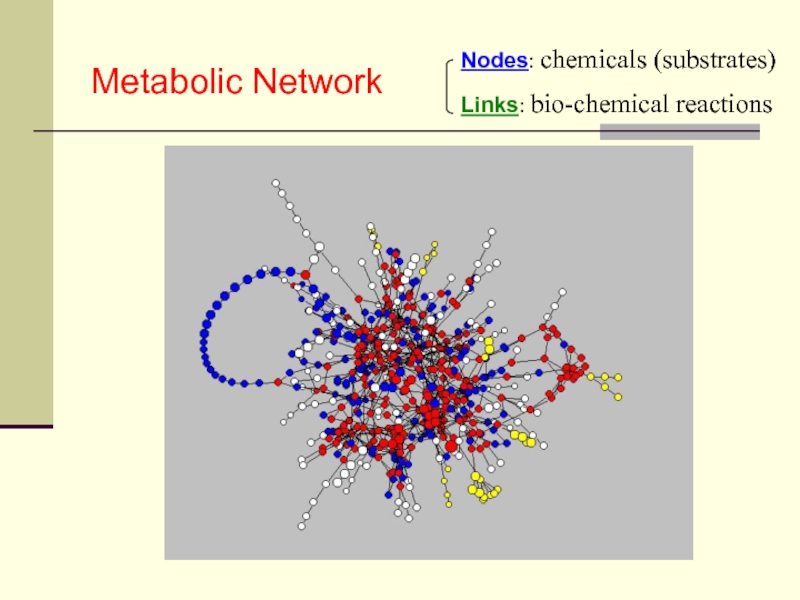
- 10. Metabolic NetworkNodes: chemicals (substrates)Links: bio-chemical reactions
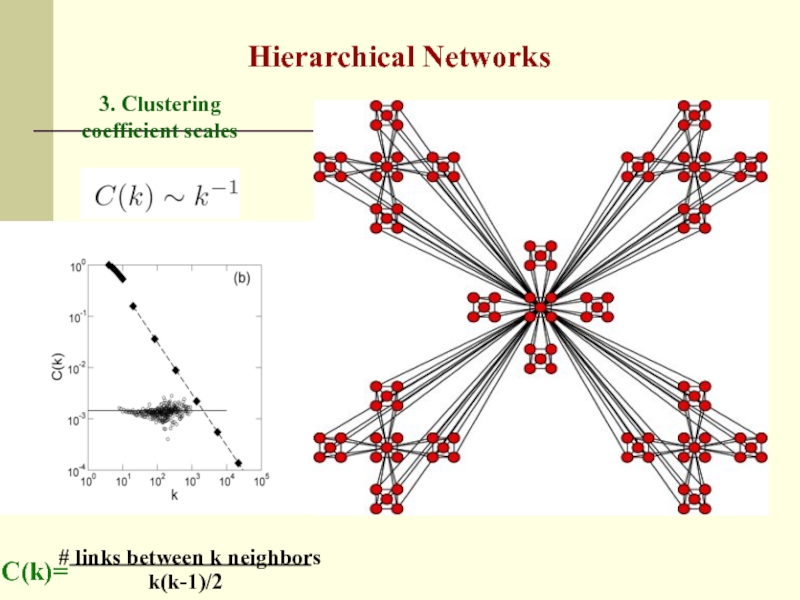
- 11. Hierarchical Networks
- 12. Internet-Map
- 13. Основные понятияГраф (от греческого — пишу)
- 14. Граф, содержащий только ребра, называется неориентированным; граф,
- 15. Каждый граф можно представить в евклидовом пространстве
- 16. Основные классы графова — обыкновенныйб — орграфв — псевдографг — мультиграфд — смешанный графе — сеть
- 17. Некоторые типы графова — полный графб —
- 18. Изоморфизм графовДва графа G(V, E) и H(W,
- 19. Подграфом G(V, E) графа G(V, E) называется
- 20. Граф называется связным, если любая пара его
- 21. ГРАФЫ И ОРИЕНТИРОВАННЫЕ ГРАФЫ (АНАЛОГИИ И
- 22. Полный путь или полный полупуть в D
- 23. Контуром в D называется замкнутый путь u1,
- 24. ПОДГРАФЫ, ОРИЕНТИРОВАННЫЕ ПОДГРАФЫ И СВЯЗНОСТЬ (АНАЛОГИИ
- 25. Подграфом в D называется орграф (W, B),
- 26. Слайд 26
- 27. Способы задания графовПусть v1, v2, ... vn
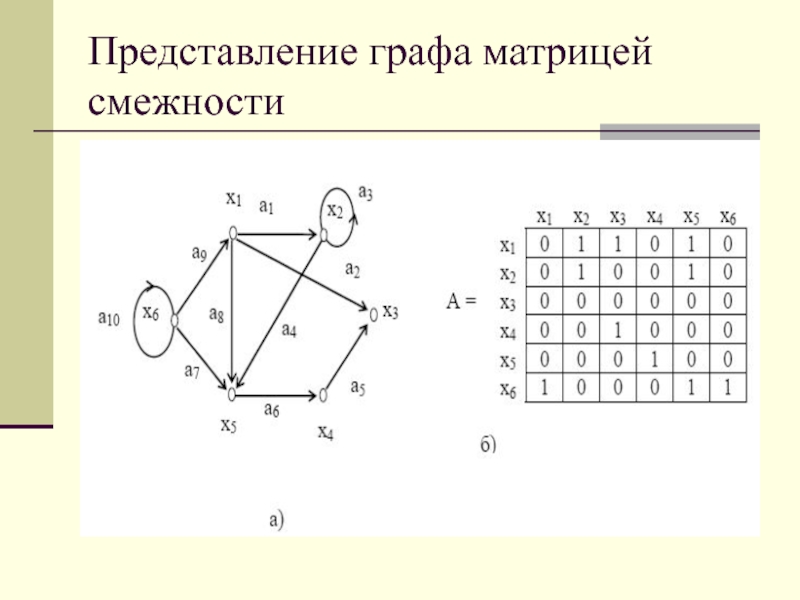
- 28. Представление графа матрицей смежности
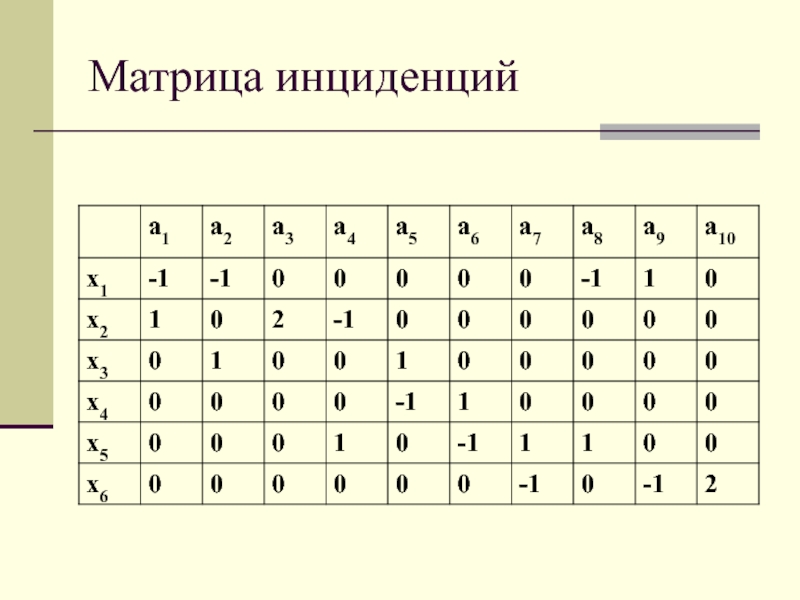
- 29. Матрица инциденций
- 30. Операции над графамиСреди одноместных операций наиболее употребительны:
- 31. Эффективность алгоритмовОдна из центральных задач информатики —
- 32. Слайд 32
- 33. Предположим, что функции f(n) и g(n) измеряют
- 34. Алгоритм нахождения эйлерова циклаИсходные данные: связный граф
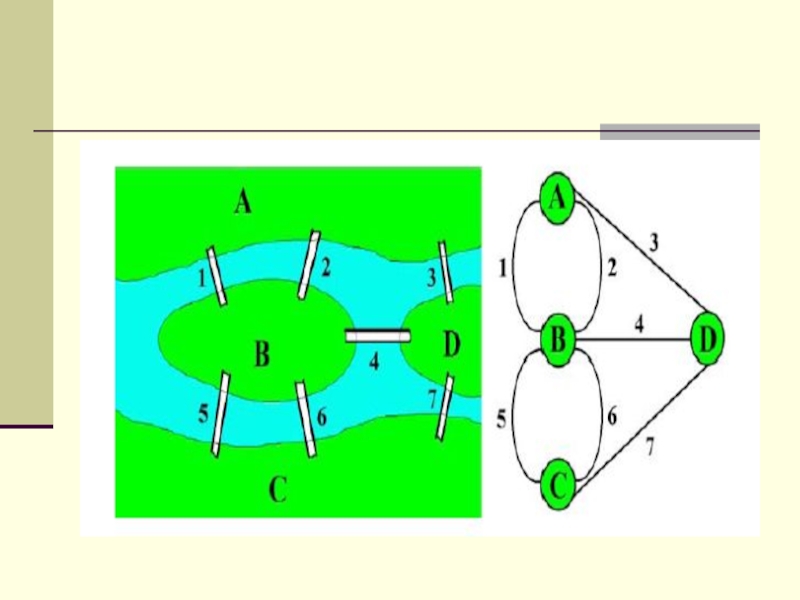
- 35. Эйлеровы циклы и путиЭйлеровым путем в графе
- 36. begin CTEK := ; СЕ :=
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Вехи
Графы Эйлера (1736)
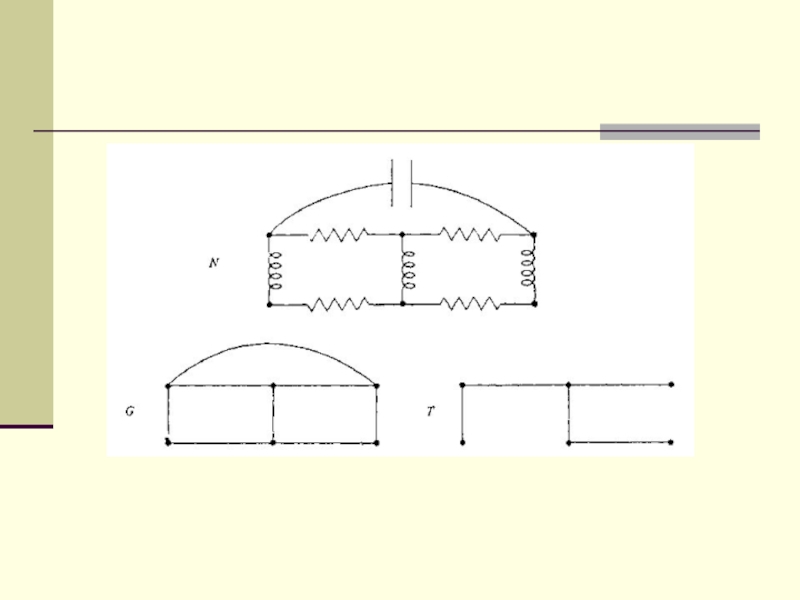
Теория Кирхгоф (1847)
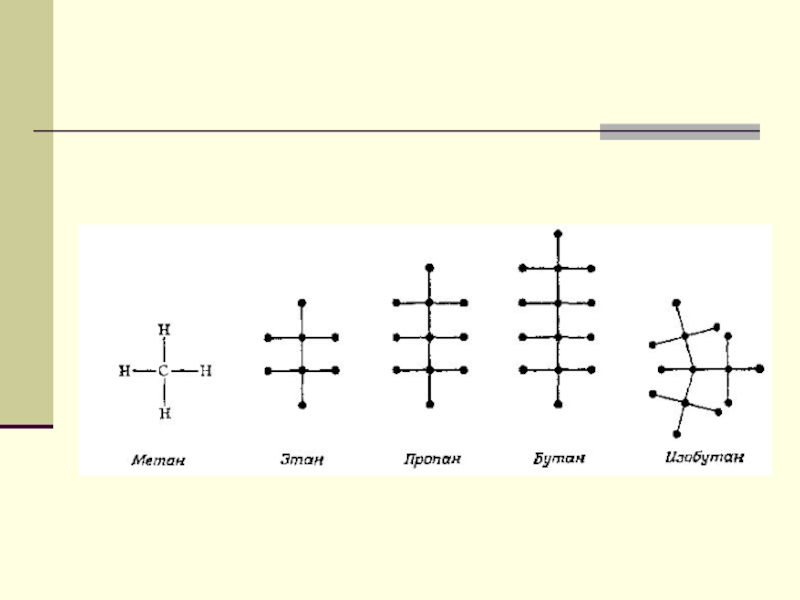
Деревья Кэли (1857) — задача о
химических изомерах
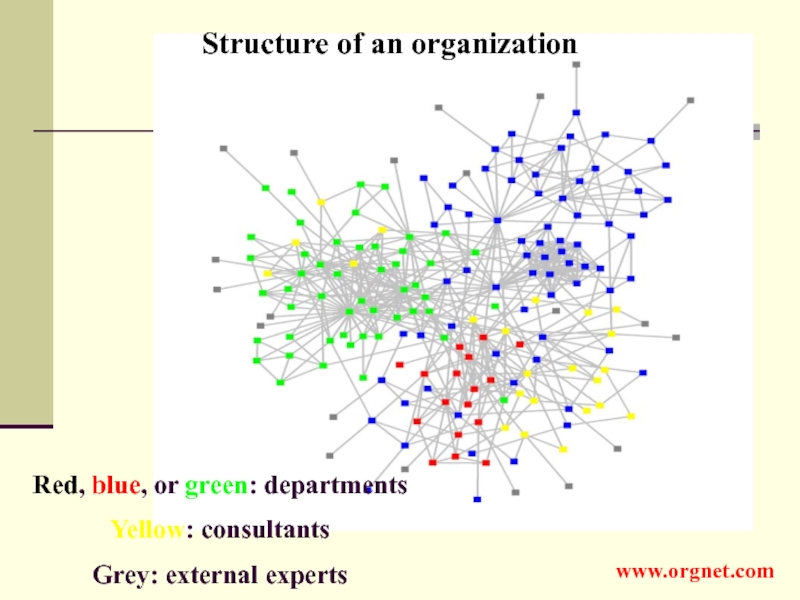
Слайд 8Red, blue, or green: departments
Yellow: consultants
Grey: external experts
Structure of an
organization
www.orgnet.com
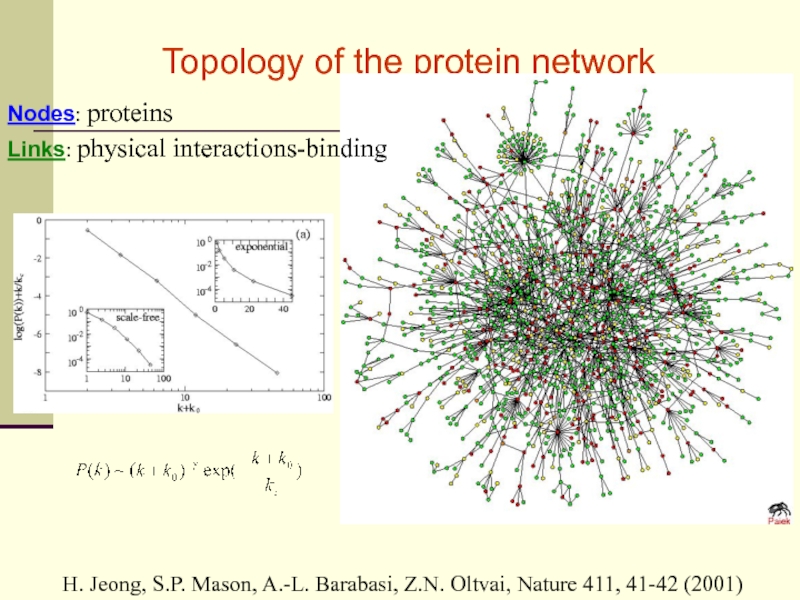
Слайд 9Topology of the protein network
H. Jeong, S.P. Mason, A.-L. Barabasi,
Z.N. Oltvai, Nature 411, 41-42 (2001)
Prot P(k)
Nodes: proteins
Links: physical interactions-binding
Слайд 13Основные понятия
Граф (от греческого — пишу) — множество V
вершин и набор E неупорядоченных и упорядоченных пар вершин; обычно
граф обозначают как G(V, E).Неупорядоченная пара вершин называется ребром, упорядоченная пара — дугой.
Слайд 14Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги
— ориентированным (или орграфом).
Пара вершин может быть соединена двумя или
более ребрами (или, соответственно, дугами одного направления), такие ребра (или дуги) называются кратными.Дуга (или ребро) может начинаться и заканчиваться в одной и той же вершине, в этом случае соотв. дуга (или ребро) называется петлей.
Вершины, соединенные ребром или дугой, называются смежными.
Ребра, имеющие общую вершину, тоже называются смежными.
Ребро (или дуга) и любая из его вершин называются инцидентными.
Принято говорить, что ребро (u, v) соединяет вершины u и v, а дуга (u, v) начинается в вершине u и кончается в вершине v.
Слайд 15Каждый граф можно представить в евклидовом пространстве множеством точек, соответствующих
вершинам, которые соединены линиями, соответствующими ребрам (или дугам — в
последнем случае направление обычно указывается стрелочками). — такое представление называется укладкой графа.Доказано, что в 3-мерном пространстве любой граф можно представить в виде укладки таким образом, что линии, соответствующие ребрам (дугам) не будут пересекаться во внутренних точках. Для 2-мерного пространства это, вообще говоря, неверно. Допускают представление в виде укладки в 2-мерном пространстве графы, называемые плоскими.
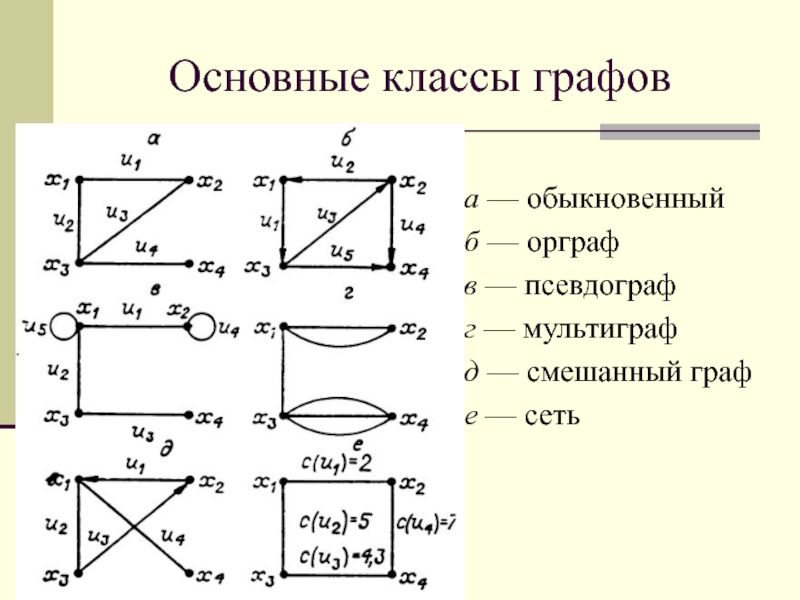
Слайд 16Основные классы графов
а — обыкновенный
б — орграф
в — псевдограф
г —
мультиграф
д — смешанный граф
е — сеть
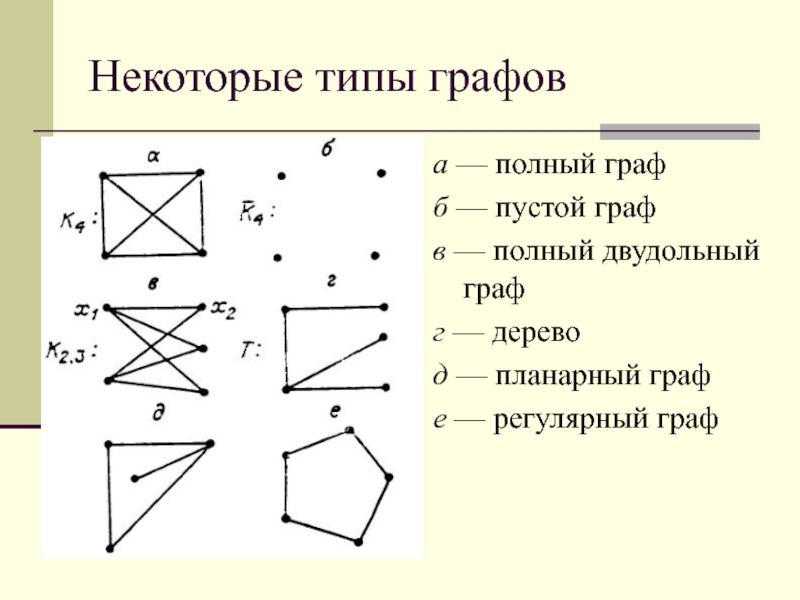
Слайд 17Некоторые типы графов
а — полный граф
б — пустой граф
в —
полный двудольный граф
г — дерево
д — планарный граф
е — регулярный
графСлайд 18Изоморфизм графов
Два графа G(V, E) и H(W, I) называются изоморфными,
если существует взаимно-однозначное соответствие между множествами вершин V, W и
множествами ребер E, I, сохраняющее отношение инцидентности.Слайд 19Подграфом G(V, E) графа G(V, E) называется граф с множеством
вершин V V и множеством ребер (дуг) E E,
— такими, что каждое ребро (дуга) из E инцидентно (инцидентна) только вершинам из V.Последовательность ребер (v0, v1), (v1, v2), ..., (vi-1, vi), (vi, vi+1), ..., (vr-1, vr) называется маршрутом, соединяющим вершины v0 и vr. Маршрут замкнут, если v0 = vr.
Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины различны.
Замкнутая (простая) цепь называется (простым) циклом.
Слайд 20Граф называется связным, если любая пара его вершин соединена маршрутом.
Любой
максимальный связный подграф (то есть, не содержащийся в других связных
подграфах) графа G называется компонентой связности. Несвязный граф имеет, по крайней мере, две компоненты связности.Связный граф с наименьшим числом ребер (или связный граф без циклов) называется деревом.
Граф называется k - связным (k - реберно - связным), если удаление не менее k вершин (ребер) приводит к потере свойства связности.
Маршрут, содержащий все вершины или ребра графа и обладающий определенными свойствами, называется обходом графа.
Длина маршрута (цепи, простой цепи) равна количеству ребер а порядке их прохождения. Длина кратчайшей простой цепи, соединяющей вершины vi и vj в графе G, называется расстоянием d (vi, vj) между vi и vj. В связном неориентированном графе расстояние удовлетворяет аксиомам метрики.
Слайд 21ГРАФЫ И ОРИЕНТИРОВАННЫЕ ГРАФЫ
(АНАЛОГИИ И ОТЛИЧИЯ)
Пусть D = (V,
A) – орграф
Путь в D – последовательность вершин и дуг
u1, a1, u2, a2,..., ut, at, ut+1 , где t0, причем каждая вершина ui V, а каждая дуга ai A, и ai всегда является дугой (ui, ui+1). Путь обычно записывается последовательностью вершин u1, u2, ..., ut, ut+1.Полупуть в D – последовательность вершин и дуг u1, a1, u2, a2,..., ut, at, ut+1, где t0, причем каждая вершина ui V, а каждая дуга ai A, и ai всегда является либо дугой (ui, ui+1), либо дугой (ui+1, ui). Полупуть также обычно записывается последовательностью вершин u1, u2, ..., ut, ut+1.
Пусть G = (V, E) – граф
Цепь в G – последовательность вершин и ребер u1, e1, u2, e2,..., ut, et, ut+1, где t0, причем каждая вершина ui V, а каждое ребро ei E, и ei всегда является ребром (ui, ui+1). Цепь обычно записывается последовательностью вершин u1, u2, ..., ut, ut+1.
Цепь = маршрут без повторений (каждое ребро проходится лишь один раз).
Аналогия — та же цепь (см. выше)
В определении полуцепи нет смысла — полуцепь всегда совпадает с соответствующей цепью.
Слайд 22Полный путь или полный полупуть в D – путь или
полупуть, проходящий через все вершины D.
Простым путем или простым полупутем
в D называется путь или полупуть без повторяющихся вершин.Замкнутым путем или полупутем в D называется путь или полупуть u1, a1, u2, a2,..., ut, at, ut+1, в котором ut+1=u1.
Полный замкнутый путь или полный замкнутый полупуть в D – полный путь или полный полупуть, который замкнут.
Полная цепь или полная полуцепь в G – цепь или полуцепь, проходящая через все вершины G.
Простой цепью в G называется цепь без повторяющихся вершин.
Замкнутой цепью в G называется цепь u1, u2, ..., ut, ut+1, в которой ut+1=u1.
Полная замкнутая цепь в G – полная цепь, которая замкнута.
Слайд 23Контуром в D называется замкнутый путь u1, u2, ..., ut,
u1, в котором все вершины различны.
Полуконтуром в D называется замкнутый
полупуть, u1, a1, u2, a2,..., ut, at, u1, в котором все вершины u1, u2, ..., ut и все дуги a1, a2,..., at различны.Вершина ui достижима из вершины uj, если имеется путь из ui в uj.
Вершины ui и uj соединимы, если имеется путь из вершины ui в вершину uj или из вершины uj в вершину ui.
Длиной пути, полупути, простого пути, простого полупути, контура или полуконтура называется число дуг, содержащихся в них.
Расстояние d(ui, uj) от вершины ui и до вершины uj в D равно длине кратчайшего пути из ui в uj или не определено, если путь из ui в uj отсутствует.
Во взвешенном графе длиной и расстоянием обычно называют с учетом веса ( весов).
Циклом в G называется замкнутая цепь u1, e1, u2, e2,..., ut, et, u1 , в которой все вершины различны.
Аналогия — тот же цикл(см. выше)
В определении полуцикла нет смысла — полуцикл всегда совпадает с соответствующим циклом.
Вершина ui, достижима из вершины uj, если имеется соединяющая их цепь.
Вершины ui и uj соединимы, если имеется соединяющая их цепь.
Длиной цепи, простой цепи или цикла называется число ребер, содержащихся в них.
Расстояние d(ui, uj) от вершины ui и до вершины uj в G равно длине кратчайшей цепи между ui и uj или не определено, если цепь между ними отсутствует.
Слайд 24ПОДГРАФЫ, ОРИЕНТИРОВАННЫЕ ПОДГРАФЫ И СВЯЗНОСТЬ
(АНАЛОГИИ И ОТЛИЧИЯ)
Орграф D называется
сильно связным (сильным, категории связности 3), если для каждой пары
вершин ui и uj в D ui достижима из uj и ui достижима из ui.Орграф D называется слабо связным (слабым, категории связности 1), если каждая пара вершин ui и uj в D соединима (полупутем).
Орграф D называется односторонне связным (односторонним, категории связности 2), если для каждой пары вершин ui и uj в D либо ui достижима из uj , либо uj достижима из ui.
Граф G называется связным, если каждая пара вершин ui и uj в G связана цепью.
Аналогия — см. выше
Аналогия — см. выше
Слайд 25Подграфом в D называется орграф (W, B), в котором W V,
B A.
Порожденным подграфом в D называется подграф (W, B), в котором
B содержит все дуги из A, соединяющие вершины в W.Сильной компонентой в D называется максимальный сильно связный (порожденный) подграф.
Подграфом в G называется граф (W, F), в котором W V, F E.
Порожденным подграфом в G называется подграф (W, F), в котором F содержит все ребра из E, соединяющие вершины в W.
Компонентой (связности) в G называется максимальный связный (порожденный) подграф.
Слайд 27Способы задания графов
Пусть v1, v2, ... vn — вершины графа
G(V, E), а e1, e2, ... em — его ребра
(дуги).Матрицей смежности вершин графа G называется матрица A=||aij||, i=1,...,n; j = 1, ..., n, у которой элемент aij равен числу ребер (или дуг), соединяющих вершины vi и vj (соответственно, идущих из вершины vi в вершину vj).
Матрицей инцидентности графа G называется матрица B=||bij||, i=1, .., n; j = 1, ..., m, у которой элемент bij равен 1, если вершина vi инцидентна ребру (дуге) ej и равен 0, если не инцидентна.
Наконец, граф можно задать посредством списков. Например,
вариант 1: списком пар вершин, соединенных ребрами (или дугами);
вариант 2: списком списков для каждой вершины множества смежных с ней вершин.
Слайд 30Операции над графами
Среди одноместных операций наиболее употребительны: удаление и добавление
ребра или вершины, стягивание ребра (отождествление пары смежных вершин), подразбиение
ребра (т.е. замена ребра (u, v) на пару (u, w), (w, v), где w — новая вершина) и др.Известны двуместные операции: соединение, сложение, различные виды умножений графов и др. Такие операции используются для анализа и синтеза графов с заданными свойствами.
Слайд 31Эффективность алгоритмов
Одна из центральных задач информатики — создание и анализ
эффективности компьютерных алгоритмов
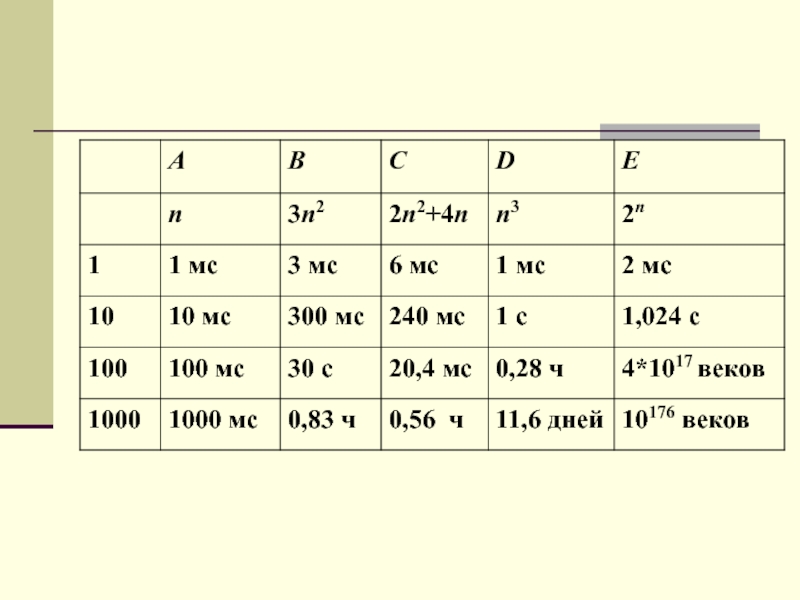
Пример. На выполнение алгоритмов А, В, С, D
и Е требуется n, 3n2, 2n2 + 4n, n3 и 2n элементарных операций соответственно.Посчитаем время, необходимое для работы алгоритмов при n = 1, 10, 100 и 1000, если одна операция совершается за 1 миллисекунду
Слайд 33Предположим, что функции f(n) и g(n) измеряют эффективность двух алгоритмов,
их обычно называют функциями временной сложности. Будем говорить, что порядок
роста функции f(n) не больше, чем у g(n), если найдется такая положительная константы С, что | f(n) | <= | g(n) |. Этот факт обозначают как f(n) = O(g(n))Слайд 34Алгоритм нахождения эйлерова цикла
Исходные данные: связный граф G = V, E без вершин
нечетной степени, представленный списками ЗАПИСЬ [v], v V.
Результаты: Эйлеров
цикл, представленный последовательностью вершин в стеке СЕ.Слайд 35Эйлеровы циклы и пути
Эйлеровым путем в графе называется произвольный путь,
проходящий через каждое ребро графа в точности один раз, т.е.
путь v1, ..., vm+1, такой что каждое ребро e E появляется в последовательности v1, ..., vm+1 в точности один раз как e = {vi, vi+1 } для некоторого i.Если v1 = vm+1, то такой путь называется эйлеровым циклом. Задача существования эйлерова пути в заданном графе была решена Эйлером в 1736 году, и представленное им необходимое и достаточное условие существования такого пути считается первой в истории теоремой теории графов.
Теорема. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечетной степени.
Слайд 36begin
CTEK := ; СЕ := ;
v:= произвольная вершина графа;
CTEK v;
while CTEK do
begin v:= top (CTEK); { v = верхний элемент стека }if ЗАПИСЬ [v] then
begin u:= первая вершина списка ЗАПИСЬ [v];
CTEK u;
{ удалить ребро {v, u} из графа }
ЗАПИСЬ [v] := ЗАПИСЬ [v] \ {u};
ЗАПИСЬ [u] := ЗАПИСЬ [u] \ {v};
v := u
end
else { ЗАПИСЬ [v] = }
begin v CTEK ; СЕ v;
end
end
end



















![Элементы теории графов Алгоритм нахождения эйлерова циклаИсходные данные: связный граф G = V, E без вершин нечетной Алгоритм нахождения эйлерова циклаИсходные данные: связный граф G = V, E без вершин нечетной степени, представленный списками ЗАПИСЬ [v], v](/img/thumbs/efc06207bee7559c9dfa5f7a61a53664-800x.jpg)