Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Содержание
- 1. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- 2. Тема 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ План
- 3. 3.1. Момент инерцииМомент инерции:- величина, характеризующая
- 4. Любое твёрдое тело состоит из множества материальных
- 5. Момент инерции твёрдого тела2. Момент инерции твёрдого
- 6. Для твёрдых тел неправильной геометрической формы массу
- 7. Элементарные массы можно представить как
- 8. Соответственно момент инерции элементарной массы запишется как
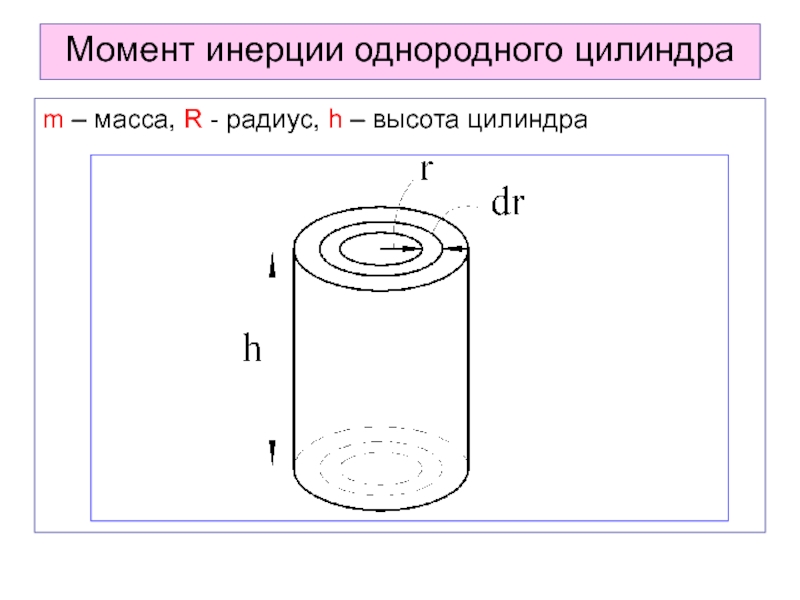
- 9. Момент инерции однородного цилиндраm – масса, R - радиус, h – высота цилиндра
- 10. Разобьем цилиндр на элементарные цилиндрические слои
- 11. Поскольку цилиндр однороден, то плотность тела
- 12. Учтем, что масса цилиндра
- 13. Моменты инерции тел правильной формыАналогично рассчитываются моменты
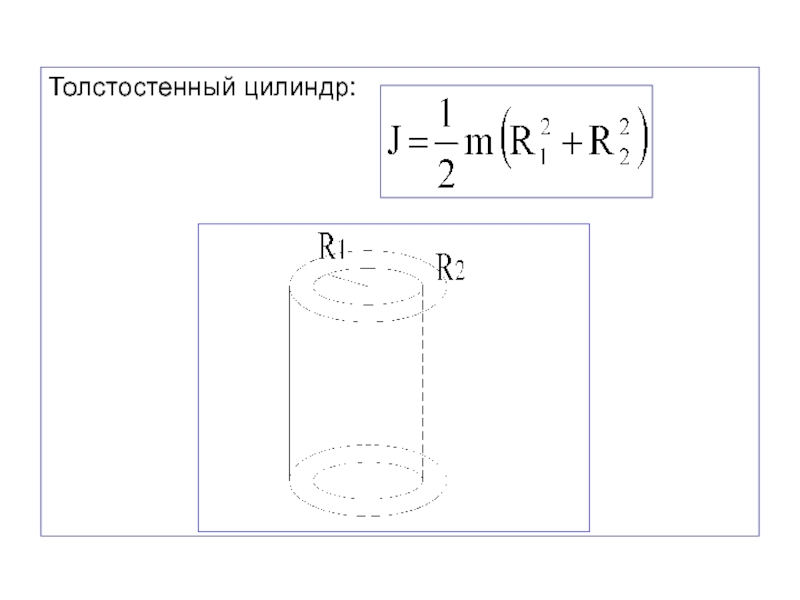
- 14. Толстостенный цилиндр:
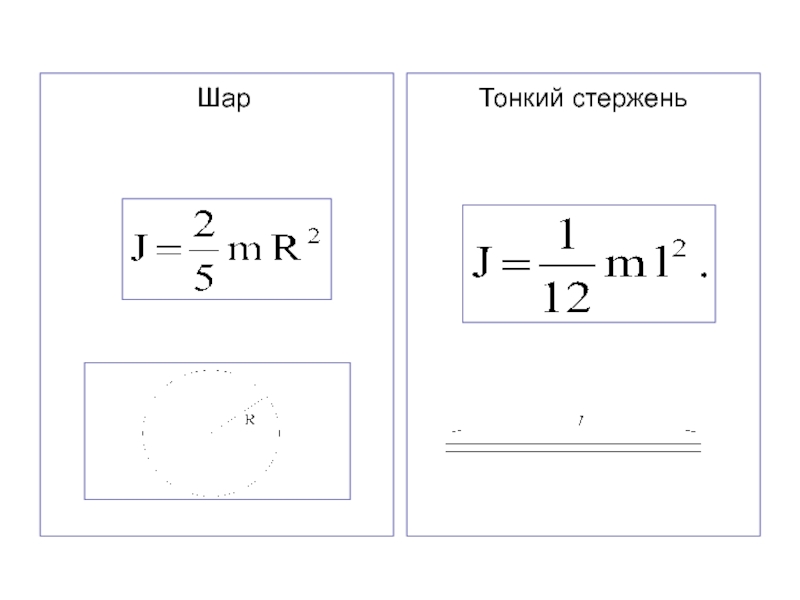
- 15. Шар Тонкий
- 16. Слайд 16
- 17. Теорема ШтейнераМоменты инерции тел относительно произвольных осей
- 18. Пример: момент инерции шара относительно оси АВ. dABCD
- 19. Таким образом, момент инерции тела зависит
- 20. 3.2. Момент силы Вращательное действие силы
- 21. Момент силы относительно точкиМоментом силы относительно некоторой
- 22. Рисунок показывает взаимное расположение векторов, если смотреть вдоль вектора момента силы.
- 23. Здесь и на последующих рисунках значком
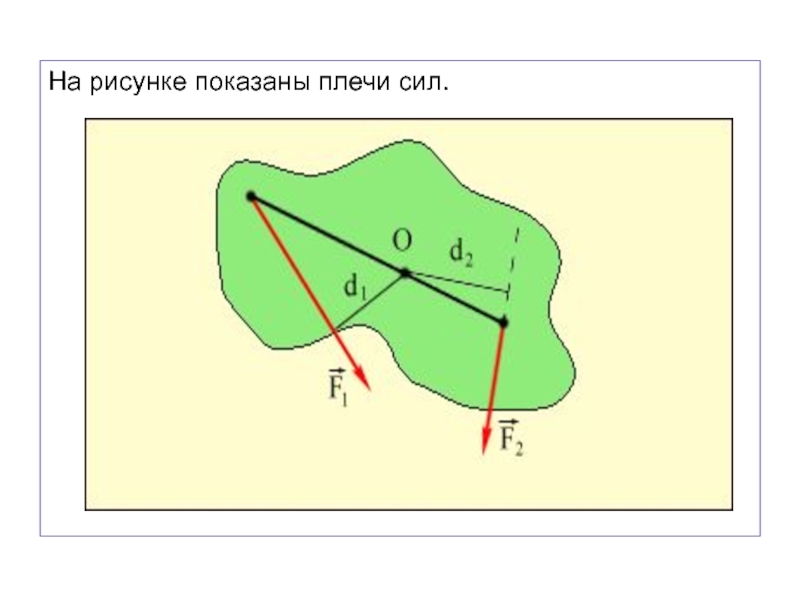
- 24. На рисунке показаны плечи сил.
- 25. Момент силы относительно оси
- 26. Моментом силы относительно некоторой оси Z называется
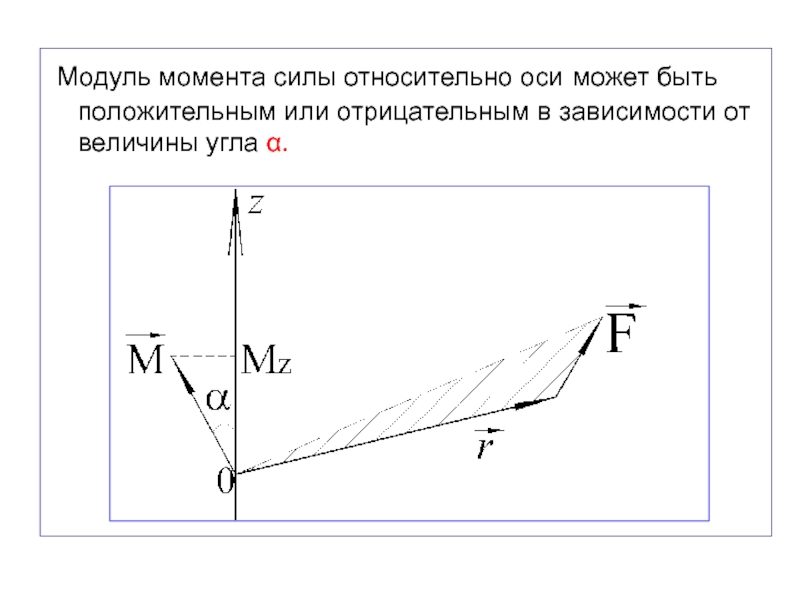
- 27. Модуль момента силы относительно оси может
- 28. Закреплённая ось вращенияВ случае, когда ось вращения
- 29. Слайд 29
- 30. В случае закреплённой оси момент силы
- 31. При этом момент силы относительно закреплённой оси
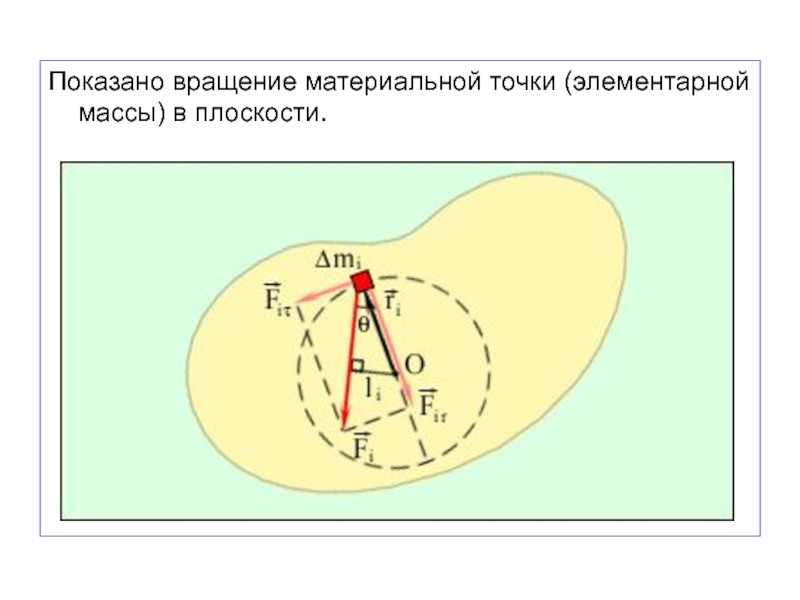
- 32. Показано вращение материальной точки (элементарной массы) в плоскости.
- 33. Момент пары силПарой сил называются две силы,
- 34. Слайд 34
- 35. Момент пары сил относительно некоторой
- 36. Пусть составляющие пару равные силы
- 37. Отсюда следует очень важный вывод о том,
- 38. 3.3. Момент импульсаМомент импульса – одна
- 39. Слайд 39
- 40. Рассмотрим два часто встречающихся на практике случая
- 41. 2. Движение материальной точки по окружности.
- 42. Момент импульса материальной точки относительно осиМоментом импульса
- 43. Модуль момента импульса относительно оси Z можно
- 44. Момент импульса твердого тела относительно оси
- 45. Выберем на оси Z произвольную точку О.Разобьем
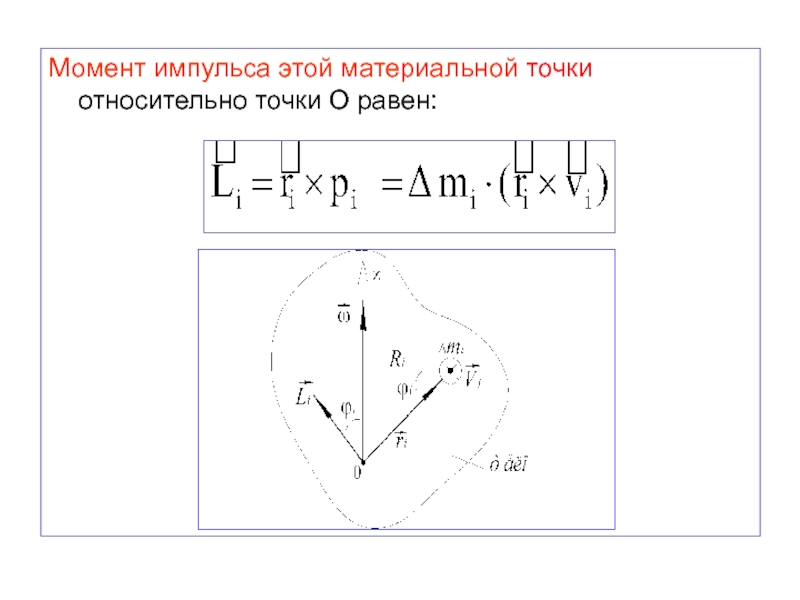
- 46. Момент импульса этой материальной точки относительно точки О равен:
- 47. Момент импульса всего тела относительно точки О
- 48. Слайд 48
- 49. Момент импульса твёрдого тела относительно закреплённой осиЗапишем
- 50. Момент импульса твёрдого тела относительно оси равен
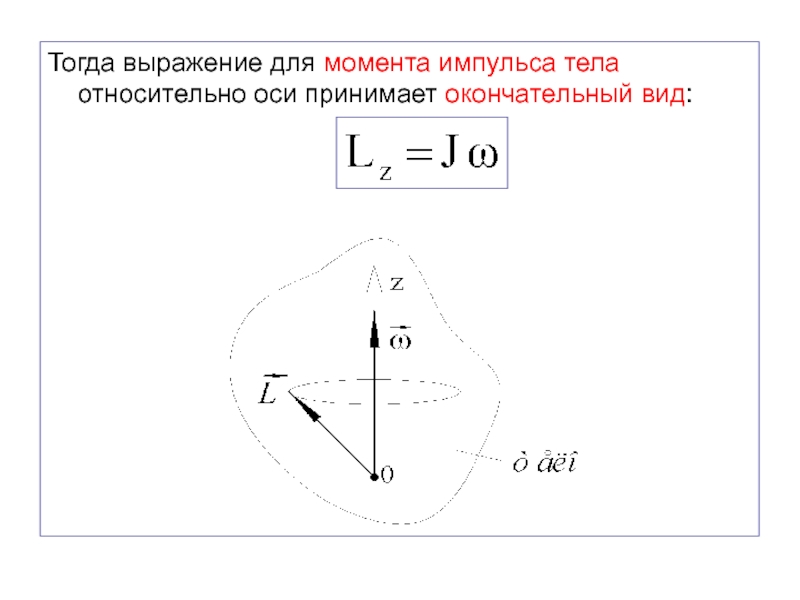
- 51. Тогда выражение для момента импульса тела относительно оси принимает окончательный вид:
- 52. 3.4. Основной закон динамики вращательного движения Пусть
- 53. Вычислим производную от вектора момента импульса по
- 54. Подобное утверждение справедливо и для момента импульса
- 55. Запишем такие же выражения для каждой точки
- 56. Слайд 56
- 57. Полученное равенство выражает наиболее общую запись основного
- 58. Момент инерции J абсолютно твердого тела
- 59. Равенство, записанное для проекций входящих величин, можно
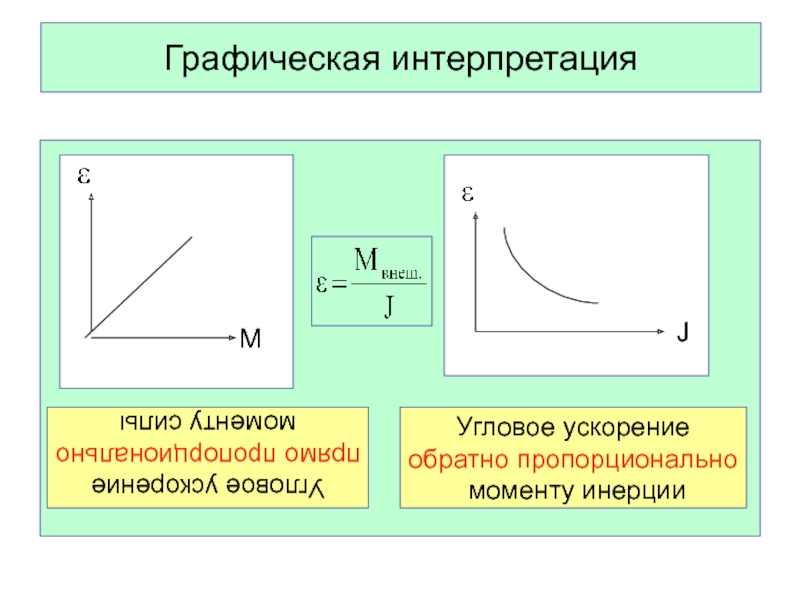
- 60. Графическая интерпретацияМУгловое ускорениепрямо пропорциональномоменту силыJУгловое ускорение обратно пропорционально моменту инерции
- 61. Условия равновесия твёрдого телаИз законов динамики поступательного
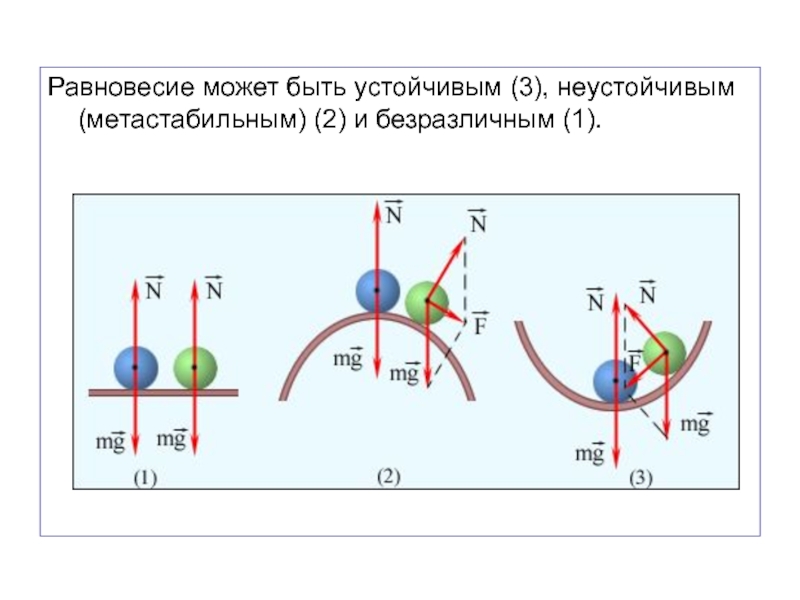
- 62. Равновесие может быть устойчивым (3), неустойчивым (метастабильным) (2) и безразличным (1).
- 63. - устойчивое положение равновесия;- неустойчивое положение равновесия.В
- 64. Скачать презентанцию
Тема 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ План лекции3.1. Момент инерции.3.2. Момент силы. 3.3. Момент импульса. 3.4. Основной закон динамики вращательного движения.
Слайды и текст этой презентации
Слайд 2Тема 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
План лекции
3.1. Момент инерции.
3.2.
Момент силы.
вращательного движения. 
Слайд 33.1. Момент инерции
Момент инерции:
- величина, характеризующая инертные свойства тела
(или материальной точки) при вращательном движении.
- скалярная величина.
1. Момент инерции
материальной точки относительно заданной оси вращения – величина, равная произведению массы этой точки на квадрат расстояния её от оси вращения:m
r
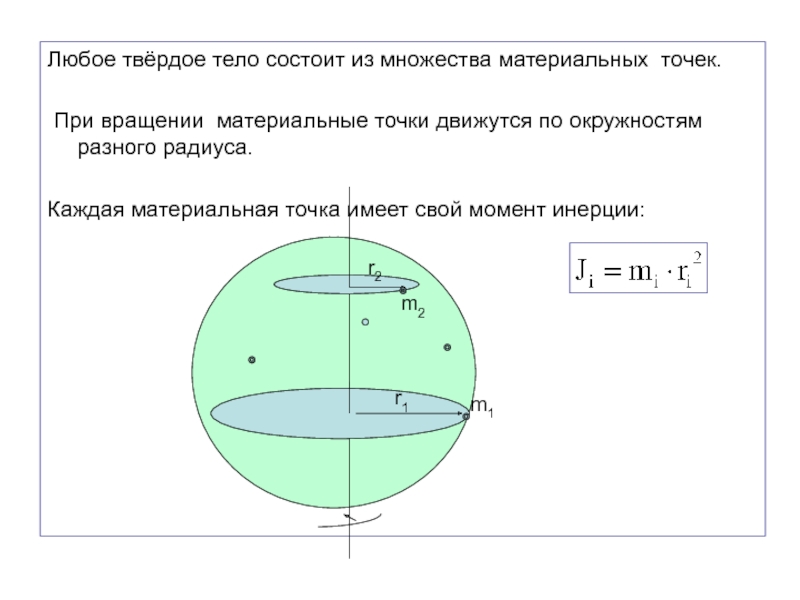
Слайд 4Любое твёрдое тело состоит из множества материальных точек.
При
вращении материальные точки движутся по окружностям разного радиуса.
Каждая материальная точка
имеет свой момент инерции:m1
m2
r1
r2
Слайд 5Момент инерции твёрдого тела
2. Момент инерции твёрдого тела относительно заданной
оси вращения равен скалярной сумме моментов инерций всех его материальных
точек относительно этой оси:Момент инерции твёрдого тела:
- скалярная величина.
- измеряется в (кг м2).
Слайд 6
Для твёрдых тел неправильной геометрической формы массу тела разбивают на
элементарные массы .
Момент инерции тела в
этом случае запишется какri - расстояние от элементарной массы до оси вращения.
Слайд 7Элементарные массы можно представить как
где – плотность тела в данной точке, – объём элементарной массы.
Следовательно,
Эти соотношения являются приближенными.
Значение момента инерции будут тем точнее, чем меньше элементарные объемы и соответствующие им элементарные массы , которые будут обозначаться как dm.
Слайд 8Соответственно момент инерции элементарной массы запишется как dJ = dm
r2 .
Тогда для твёрдых тел правильной геометрической формы вычисление момента
инерции тела сводится к вычислению интеграла:В качестве примера найдем момент инерции однородного цилиндра относительно оси, совпадающей с осью его симметрии.
Слайд 10 Разобьем цилиндр на элементарные цилиндрические слои массой dm, расположенные
в элементарных объемах dV.
Все точки одного слоя будут находиться на
одинаковом расстоянии r от оси цилиндра. Объем такого слоя равен:
r
dr
Слайд 11 Поскольку цилиндр однороден, то плотность тела
.
R – радиус цилиндра.
Вынесем за знак интеграла постоянные величины:
Слайд 12Учтем, что масса цилиндра
В итоге получим формулу момента инерции сплошного цилиндра относительно оси, проходящей через его центр тяжести в виде:
m
R
Слайд 13Моменты инерции тел правильной формы
Аналогично рассчитываются моменты инерции любых тел
правильной формы.
Дальше приведены формулы моментов инерции некоторых тел правильной
геометрической формы.Тонкий цилиндр и обруч
Слайд 17Теорема Штейнера
Моменты инерции тел относительно произвольных осей рассчитываются по теореме
Штейнера:
Момент инерции J относительно произвольной оси равен сумме момента инерции
J0 относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями.d
Слайд 19
Таким образом, момент инерции тела зависит от его формы,
размеров, плотности, расположения оси вращения.
Момент инерции не зависит от
характера движения тела.
Слайд 203.2. Момент силы
Вращательное действие силы – сообщение телу
углового ускорения – зависит не только от модуля и направления
силы, но и от того, к какой точке тела она приложена.Величиной, которая учитывает все эти факторы, является момент силы - М.
Момент силы:
- величина векторная;
- измеряется в Нм (ньютон - метрах).
Слайд 21Момент силы относительно точки
Моментом силы относительно некоторой точки О называется
векторное произведение радиус-вектора, проведенного из точки О в точку приложения
силы, на вектор силы.
Слайд 22 Рисунок показывает взаимное расположение векторов, если смотреть вдоль
вектора момента силы.
Слайд 23Здесь и на последующих рисунках значком
обозначено направление вектора момента силы –
«от нас».
Модуль момента
силы равен произведению величины силы на её плечо. l – плечо силы F (длина перпендикуляра, опущенного из точки О на линию действия силы).
Слайд 26Моментом силы относительно некоторой оси Z называется проекция момента силы
относительно любой точки, взятой на данной оси, на эту ось
Z:Момент силы относительно оси – величина скалярная, не имеющая направления.
Слайд 27 Модуль момента силы относительно оси может быть положительным или
отрицательным в зависимости от величины угла α.
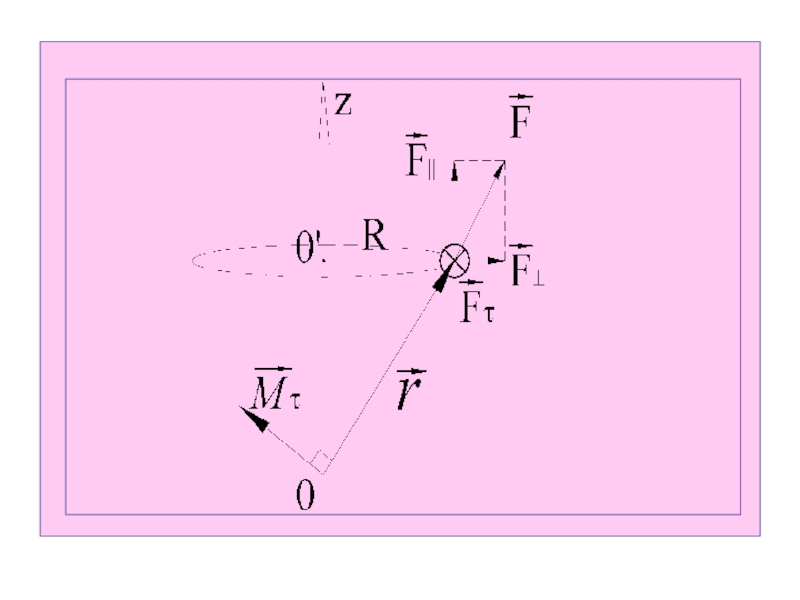
Слайд 28Закреплённая ось вращения
В случае, когда ось вращения закреплена, силу следует
представить в виде суммы трех векторов:
F║ - направленного вдоль
оси вращения, F┴ - перпендикулярного оси вращения,
Fτ - направленного по касательной к окружности, вдоль которой движется точка приложения силы.
Слайд 30
В случае закреплённой оси момент силы
относительно произвольной точки О равен сумме трёх моментов составляющих
сил:М = М║ + М┴ + Мτ
Не равен нулю только момент составляющей .
Тогда
Слайд 31
При этом момент силы относительно закреплённой оси Z будет равен
Здесь Fτ – проекция составляющей
на направление перемещения точки приложения силы.
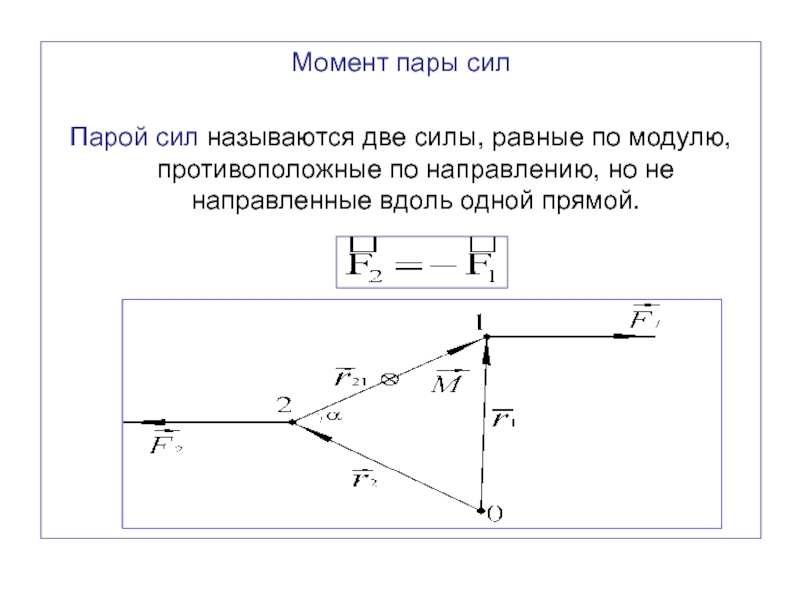
Слайд 33Момент пары сил
Парой сил называются две силы, равные по модулю,
противоположные по направлению, но не направленные вдоль одной прямой.
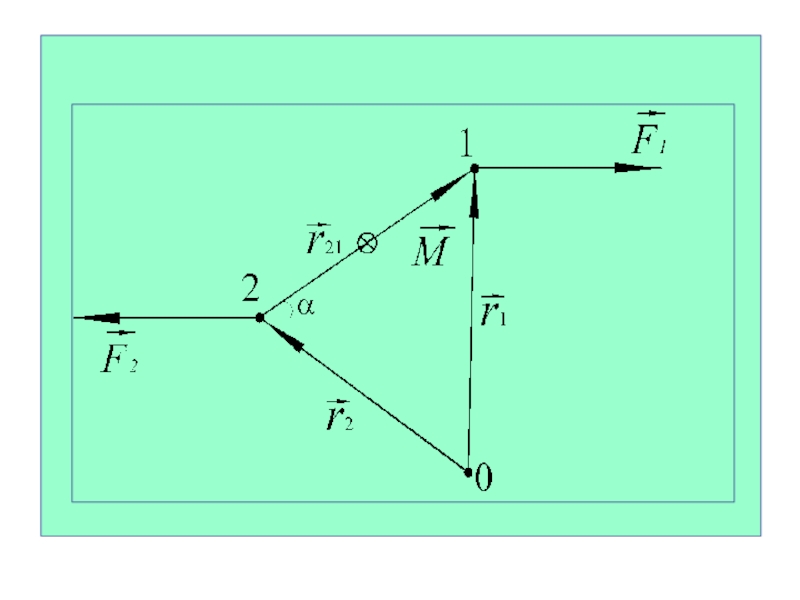
Слайд 35
Момент пары сил относительно некоторой точки О равен
сумме моментов сил, образующих пару.
Сделаем преобразования:
Момент пары сил не
зависит от положения точки О. Его направление показано значком (от нас).
Слайд 36Пусть составляющие пару равные силы
направлены вдоль одной прямой в противоположные
стороны.Тогда вектор параллелен вектору силы .
Их векторное произведение при этом равно нулю.
r21
F2
F1
1
2
Слайд 37Отсюда следует очень важный вывод о том, что сумма моментов
всех внутренних сил для любой системы частиц равна нулю.
Слайд 383.3. Момент импульса
Момент импульса – одна из важнейших физических
величин.
Различают момент импульса материальной точки относительно точки и относительно оси.
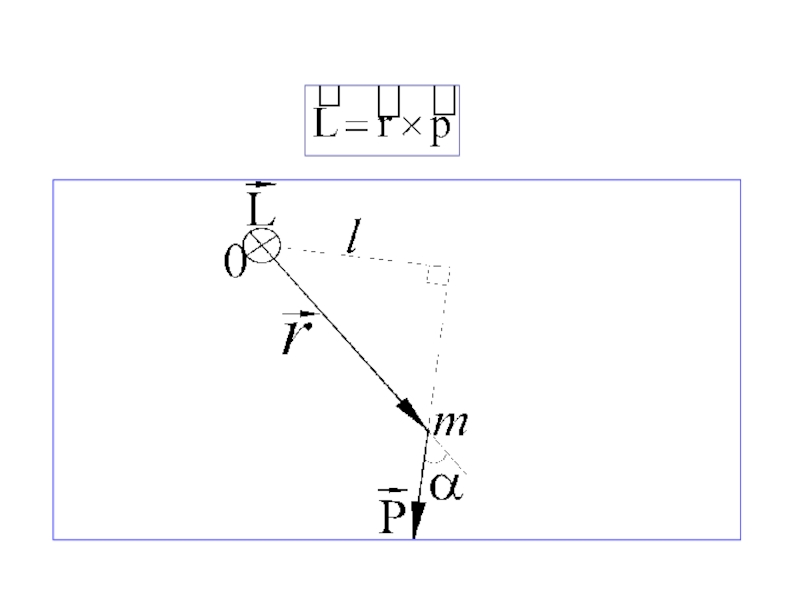
Моментом импульса материальной точки относительно некоторой точки О называется векторное произведение радиуса – вектора, проведённого из точки О к данной материальной точке, на вектор импульса этой материальной точки.
Слайд 40Рассмотрим два часто встречающихся на практике случая движения материальной точки:
1. Движение материальной точки по прямолинейной траектории.
Вектор момента импульса направлен
от нас, а его модуль равен Расстояние l называется прицельным параметром.
Слайд 41 2. Движение материальной точки по окружности.
В этом случае
угол между радиус-вектором материальной точки и импульсом
этой точки равен 900 , поэтому модуль момента импульса равенr – радиус окружности, по которой происходит движение.
Слайд 42Момент импульса материальной точки относительно оси
Моментом импульса материальной точки относительно
произвольной оси Z называется проекция вектора момента импульса этой материальной
точки относительно любой точки О, выбранной на оси Z, на данную ось.
Слайд 43
Модуль момента импульса относительно оси Z можно записать как
где
pτ – проекция импульса на направление вектора, направленного по касательной
к окружности радиусом R, проведенной через материальную точку перпендикулярно оси вращения.Направление вектора образует с осью Z правовинтовую систему.
Слайд 44 Момент импульса твердого тела относительно оси вращения
Момент импульса твёрдого
тела относительно оси вращения равен векторной сумме моментов импульсов всех
материальных точек, из которых состоит твёрдое тело.
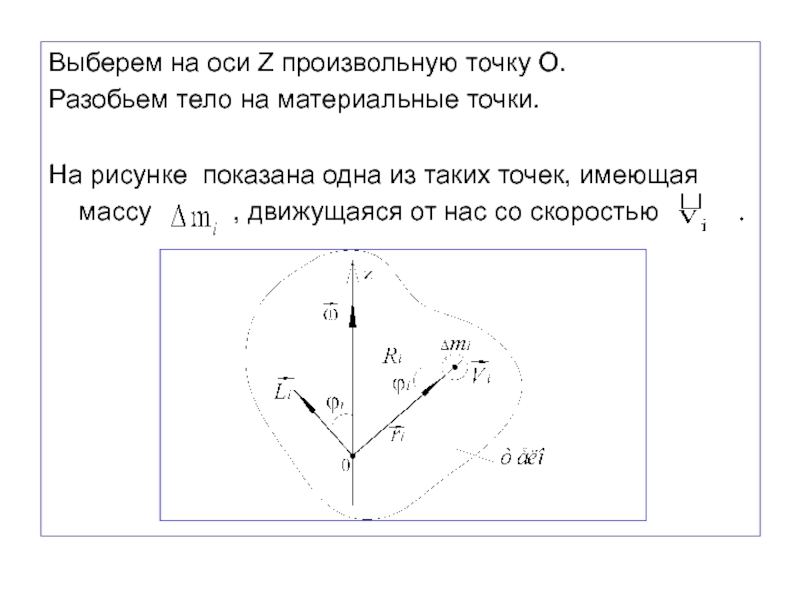
Слайд 45Выберем на оси Z произвольную точку О.
Разобьем тело на материальные
точки.
На рисунке показана одна из таких точек, имеющая массу
, движущаяся от нас со скоростью .
Слайд 47Момент импульса всего тела относительно точки О равен векторной сумме
моментов импульсов всех материальных точек:
Заметим, что в общем случае
для несимметричного тела момент импульса тела относительно точки О не направлен вдоль оси вращения тела и при вращении описывает вокруг оси Z коническую поверхность.
Слайд 49Момент импульса твёрдого тела относительно закреплённой оси
Запишем выражение для момента
импульса отдельной материальной точки относительно оси Z.
Учтем взаимосвязь модулей угловой и линейной скоростей материальной точки:
Тогда
Слайд 50Момент импульса твёрдого тела относительно оси равен скалярной сумме моментов
импульсов всех точек этого тела относительно этой оси:
Момент импульса тела относительно оси не зависит от выбора положения точки О.
Сумма в последнем равенстве представляет собой момент инерции тела относительно оси Z.
Слайд 523.4. Основной закон динамики вращательного движения
Пусть твёрдое тело
вращается вокруг закреплённой оси.
Разобьём тело на материальные точки.
Момент импульса материальной
точки относительно оси вращения определяется выражением:Выясним, от чего зависит изменение момента импульса материальной точки.
Слайд 53Вычислим производную от вектора момента импульса по времени:
Скорость изменения момента
импульса материальной точки равна моменту сил, действующих на эту точку.
Слайд 54Подобное утверждение справедливо и для момента импульса материальной точки относительно
некоторой оси Z.
Другая формулировка: изменение момента импульса равно импульсу момента
приложенной силы:
Слайд 55Запишем такие же выражения для каждой точки вращающегося тела, а
затем просуммируем по всем точкам тела:
В последнем равенстве Lz –
момент импульса тела относительно оси Z.
Слайд 56
– сумма моментов
внутренних сил равна нулю.– сумма моментов внешних сил.
Тогда для всего тела в целом имеем равенство:
Слайд 57
Полученное равенство выражает наиболее общую запись основного закона динамики вращательного
движения.
Формулировка закона: скорость изменения момента импульса твёрдого тела относительно
оси вращения равна результирующему моменту внешних сил, действующих на это тело относительно этой же оси.Учтем, что
Слайд 58Момент инерции J абсолютно твердого тела – постоянная величина.
Вынесем
её за знак дифференциала:
Обозначим
εz – проекция вектора углового ускорения на ось Z, направленную по вектору угловой скорости.
Окончательно получим:
Слайд 59
Равенство, записанное для проекций входящих величин, можно записать и для
модулей и для векторов этих величин:
Другая формулировка основного закона динамики
вращательного движения закона: угловое ускорение твёрдого тела при его вращении вокруг закреплённой оси прямо пропорционально результирующему моменту внешних сил относительно этой же оси и обратно пропорционально моменту инерции тела.
Слайд 60Графическая интерпретация
М
Угловое ускорение
прямо пропорционально
моменту силы
J
Угловое ускорение
обратно пропорционально
моменту инерции
Слайд 61Условия равновесия твёрдого тела
Из законов динамики поступательного и вращательного движений
следуют условия равновесия тел.
Тело находится в покое (не движется поступательно
и не вращается), если результирующая внешних сил равна нулю (первое условие равновесия) и результирующий момент внешних сил равен нулю (второе условие равновесия).
Слайд 63- устойчивое положение равновесия;
- неустойчивое положение равновесия.
В первом случае точки
приложения сил находятся на прямой, проходящей через центр тяжести, во
втором случае – в разных точках.
