Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Второе начало термодинамики
Содержание
- 1. Второе начало термодинамики
- 2. Тепловая машина – периодически действующий двигатель, предназначенный
- 3. Условная схема тепловой машины и ее термодинамический
- 4. ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫКоэффициент полезного действия цикла
- 5. ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ. Холодильная машина -
- 6. 1850 г., Р. Клаузиус: Теплота не
- 7. Обратимый процесс – процесс, в результате которого
- 8. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ Необратимые процессы
- 9. За весь цикл производится работа:Цикл Карно
- 10. Первая теорема Карно: Коэффициент полезного действия любой обратимой
- 11. 1-2: изотермическое нагревание2-3: адиабатное расширение3-4: изотермическое сжатие4-1: адиабатное сжатиеЦИКЛ КАРНО. ТЕОРЕМЫ КАРНО
- 12. 2-3:4-1:[26][28]Вторая теорема Карно: КПД любой тепловой машины,
- 13. Неравенство Клаузиуса - приведенное количество теплоты в
- 14. [26], [28]Неравенство Клаузиуса [30]Приведенное количество теплоты, полученное
- 15. Неравенство Клаузиуса Можно показать, что утверждения, сделанные
- 16. Энтропия.[34]Пусть процесс 1а2b - обратимый[31]Энтропия – это
- 17. Энтропия[32][36]Обобщая (35) и (36) на любые процессы:Если процесса 1а2 - обратимый, а 2b1 – необратимый[37]
- 18. Энтропия идеального газаУравнение (37) в дифференциальном виде:СV – молярная теплоемкость идеального газа [38][39]
- 19. .Закон возрастания энтропииВ адиабатически изолированной системе δQ
- 20. Статистический смысл энтропии С точки зрения теории
- 21. Скачать презентанцию
Тепловая машина – периодически действующий двигатель, предназначенный для преобразования в полезную работу теплоты, получаемой извне (выделяемой вследствие сгорания топлива, ядерных превращений, нагрева солнечными лучами и т. д).Обязательные составляющие тепловой машины: рабочее тело
Слайды и текст этой презентации
Слайд 1ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Тепловые и холодильные машины.
Второе начало термодинамики.
Обратимые и необратимые
процессы.
смысл энтропии.
Слайд 2Тепловая машина – периодически действующий двигатель, предназначенный для преобразования в
полезную работу теплоты, получаемой извне (выделяемой вследствие сгорания топлива, ядерных
превращений, нагрева солнечными лучами и т. д).Обязательные составляющие тепловой машины:
рабочее тело
нагреватель
холодильник
ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
Примеры: двигатель внутреннего сгорания,
Слайд 3Условная схема тепловой машины и ее термодинамический цикл:
ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ
МАШИНЫ
Работа газа за цикл:
Qн – количество теплоты, полученное от нагревателя;
Qх
– количество теплоты, отданное холодильнику.
Слайд 4
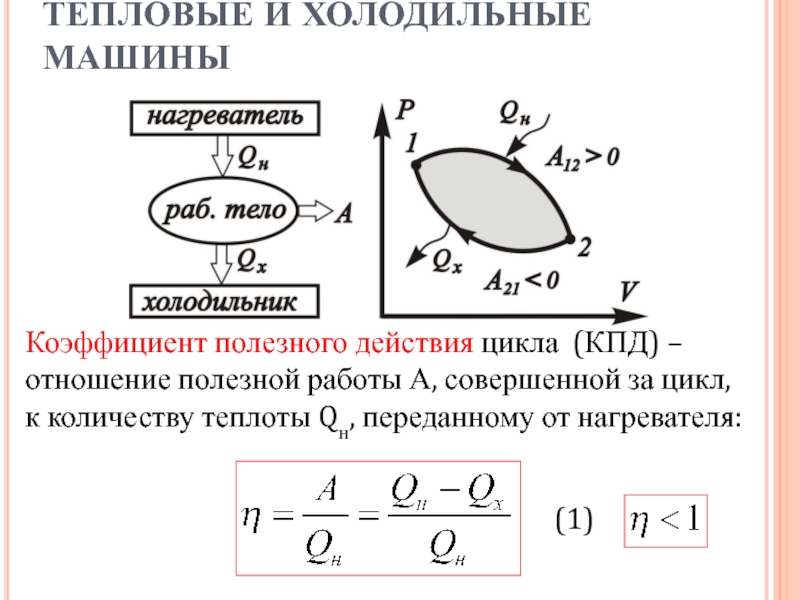
ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
Коэффициент полезного действия цикла (КПД) – отношение
полезной работы А, совершенной за цикл, к количеству теплоты Qн,
переданному от нагревателя:(1)
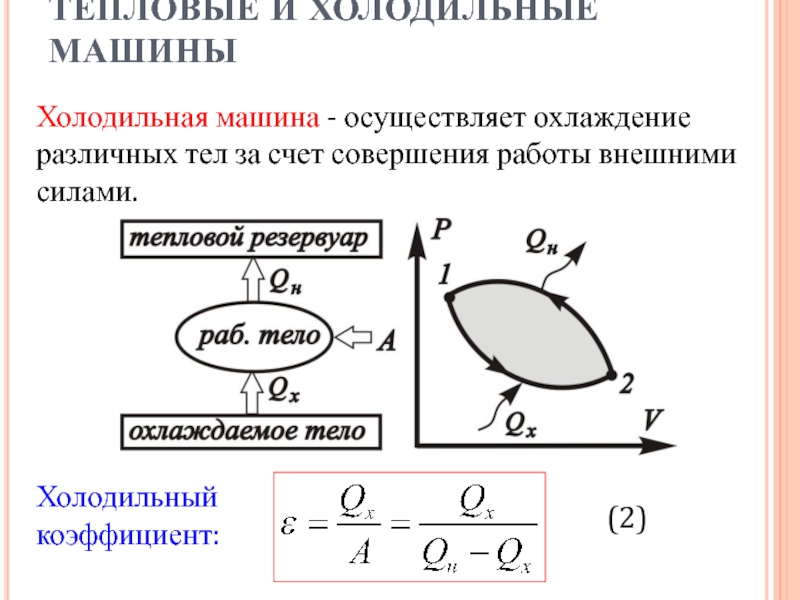
Слайд 5ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
.
Холодильная машина - осуществляет охлаждение различных
тел за счет совершения работы внешними силами.
Холодильный
коэффициент:
(2)
Слайд 6
1850 г., Р. Клаузиус:
Теплота не может самопроизвольно перейти
от более холодного тела к более теплому.
1851 г., В.
Томсон (лордом Кельвин): В природе невозможен круговой процесс, единственным результатом которого была бы механическая работа, совершаемая за счет отвода теплоты от теплового резервуара.
.
Невозможность создания тепловой машины, которая бы полностью преобразовывала теплоту в работу. Такая тепловая машина с η = 1 называется вечным двигателем второго рода.
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Слайд 7Обратимый процесс – процесс, в результате которого система переходит из
одного состояния в другое и возможен обратный процесс, в результате
которого она, пройдя через ту же последовательность промежуточных состояний, вернется в исходное состояние так, что в окружающих телах не произойдет никаких изменений. В противном случае процесс называется необратимым.Квазистатический (равновесный) процесс - ≡ обратим.
ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ
Слайд 8ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ
Необратимые процессы возникают в системах, в
которых наблюдается нарушение состояния равновесия, и возникают потоки частиц, энергии
и т. д.Пример необратимого процесса в механике: колебание маятника. Если трения нет, процесс является обратимым
Слайд 9
За весь цикл производится работа:
Цикл Карно – состоит из
двух изотерм и двух адиабат.
ЦИКЛ КАРНО. ТЕОРЕМЫ КАРНО
Слайд 10Первая теорема Карно: Коэффициент полезного действия любой обратимой тепловой машины, работающей
по циклу Карно, не зависит от природы рабочего тела и
устройства машины, а является функцией только температуры нагревателя и холодильника.ЦИКЛ КАРНО. ТЕОРЕМЫ КАРНО
Слайд 111-2: изотермическое нагревание
2-3: адиабатное расширение
3-4: изотермическое сжатие
4-1: адиабатное сжатие
ЦИКЛ КАРНО.
ТЕОРЕМЫ КАРНО
Слайд 12
2-3:
4-1:
[26]
[28]
Вторая теорема Карно: КПД любой тепловой машины, работающей по необратимому
циклу, меньше КПД машины с обратимым циклом Карно с теми
же самыми температурами нагревателя и холодильника:[29]
ЦИКЛ КАРНО. ТЕОРЕМЫ КАРНО
![2-3:4-1:[26][28]Вторая теорема Карно: КПД любой тепловой машины, работающей по необратимому циклу, меньше КПД машины с обратимым циклом](/img/thumbs/64996dc0cab23c96d7c49b37941efaf1-800x.jpg "Второе начало термодинамики 2-3:4-1:[26][28]Вторая теорема Карно: КПД любой тепловой машины, работающей по необратимому циклу,")
Слайд 13Неравенство Клаузиуса
- приведенное количество теплоты в процессе 1-2
δQ
– теплота, переданная системе от резервуара с температурой Т.
Для обратимого
цикла Карно:За весь цикл:
[30]
Слайд 14[26], [28]
Неравенство Клаузиуса
[30]
Приведенное количество теплоты, полученное системой в обратимом
цикле Карно, равно нулю.
Для необратимого цикла Карно:
.
Приведенное количество теплоты,
полученное системой в необратимом цикле Карно, меньше нуля. ![[26], [28]Неравенство Клаузиуса [30]Приведенное количество теплоты, полученное системой в обратимом цикле Карно, равно нулю. Для необратимого цикла](/img/thumbs/1a86379a4b31d359f6d1eba9e9a41a27-800x.jpg "Второе начало термодинамики [26], [28]Неравенство Клаузиуса [30]Приведенное количество теплоты, полученное системой в обратимом цикле")
Слайд 15Неравенство Клаузиуса
Можно показать, что утверждения, сделанные относительно приведенного количества
теплоты, полученного системой за цикл Карно справедливы и для любых
круговых процессов.Для любого обратимого
кругового процесса:
Для любого необратимого
кругового процесса:
Приведенное количество теплоты в замкнутом цикле для любой термодинамической системы не может быть больше нуля:
[31]
- неравенство Клаузиуса
[32]
[33]
Слайд 16Энтропия
.
[34]
Пусть процесс 1а2b - обратимый
[31]
Энтропия – это функция состояния термодинамической
системы, приращение S2 – S1 которой равно приведенному количеству теплоты,
которое нужно сообщить системе, чтобы перевести ее из состояния 1 в состояние 2 по любому обратимому пути:[35]
![Энтропия.[34]Пусть процесс 1а2b - обратимый[31]Энтропия – это функция состояния термодинамической системы, приращение S2 – S1 которой равно](/img/thumbs/e587f2a2254c01ccd21188e990a6d7cb-800x.jpg "Второе начало термодинамики Энтропия.[34]Пусть процесс 1а2b - обратимый[31]Энтропия – это функция состояния термодинамической системы,")
Слайд 17Энтропия
[32]
[36]
Обобщая (35) и (36) на любые процессы:
Если процесса 1а2 -
обратимый, а
2b1 – необратимый
[37]
![Энтропия[32][36]Обобщая (35) и (36) на любые процессы:Если процесса 1а2 - обратимый, а 2b1 – необратимый[37]](/img/thumbs/2d9ff1e01342edc081251fb98342761f-800x.jpg "Второе начало термодинамики Энтропия[32][36]Обобщая (35) и (36) на любые процессы:Если процесса 1а2 - обратимый, а 2b1 – необратимый[37]")
Слайд 18Энтропия идеального газа
Уравнение (37) в дифференциальном виде:
СV – молярная теплоемкость
идеального газа
[38]
[39]
![Энтропия идеального газаУравнение (37) в дифференциальном виде:СV – молярная теплоемкость идеального газа [38][39]](/img/thumbs/49e7e69a2b94e780d9544d29cdebb487-800x.jpg "Второе начало термодинамики Энтропия идеального газаУравнение (37) в дифференциальном виде:СV – молярная теплоемкость идеального газа [38][39]")
Слайд 19.
Закон возрастания энтропии
В адиабатически изолированной системе δQ = 0
[37]
Закон возрастания
энтропии: В адиабатически изолированной термодинамической системе энтропия не может убывать: она
или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.![.Закон возрастания энтропииВ адиабатически изолированной системе δQ = 0[37]Закон возрастания энтропии: В адиабатически изолированной термодинамической системе энтропия не](/img/thumbs/174eaf344dc917c9ff3a3771386936ba-800x.jpg "Второе начало термодинамики .Закон возрастания энтропииВ адиабатически изолированной системе δQ = 0[37]Закон возрастания энтропии: В")
Слайд 20Статистический смысл энтропии
С точки зрения теории вероятностей состояния с
большей энтропией обладают большей вероятностью.
Между энтропией системы S и вероятностью
того же состояния Р существует связь:Статистический вес Ω макросостояния, число равновесных микросостояний, с помощью которых может быть реализовано рассматриваемое макросостояние.
Один моль О2 при н.у.:
Р ~ Ω
формула Больцмана
Флуктуации – случайные отклонения макроскопических параметров от средних значений
