Слайд 11. КИНЕМАТИКА
1.1 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Кинематикой называют раздел механики, изучающий
способы (не причины!) описания движений и связь между величинами, характеризующими
эти движения.
МОДЕЛИ МЕХАНИЧЕСКИХ СИСТЕМ:
Материальная точка (МТ) – любой объект, формой и размерами которого в данной задаче (в данных условиях) можно пренебречь;
Набор конечного числа материальных точек – достаточно общая модель произвольной механической системы.
Абсолютно твёрдое тело (АТТ) – тело, форма и размеры которого при наличии тех воздействий, что описаны в условиях задачи, могут считаться неизменными. АТТ можно рассматривать как набор материальных точек с неизменными расстояниями между ними.
Система отсчета - тело отсчёта, жёстко связанная с ним система координат и часы
Слайд 2О – начало координат (начало отсчёта); K – название системы
отсчёта
Положение МТ в пространстве в определённый момент времени задаётся тремя
её координатами (например, декартовыми) или радиус-вектором :
, , . (1.1)
При движении МТ её координаты становятся функциями времени:
, , . (1.2 а, б, в)
Аналогично,
. (1.3)
Закон движения МТ – правило, по которому можно определить её положение в любой момент времени.
P.S. Закон движения (1.2 а, б, в) можно рассматривать как уравнения траектории, заданной в параметрическом виде (в роли параметра t).
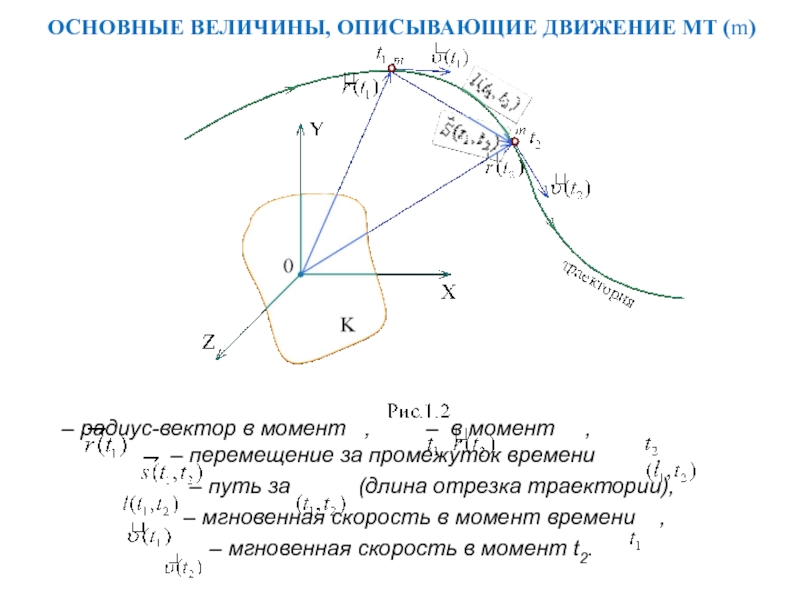
Слайд 3ОСНОВНЫЕ ВЕЛИЧИНЫ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ МТ (m)
– радиус-вектор в момент
, – в момент
, – перемещение за промежуток времени ,
– путь за (длина отрезка траектории),
– мгновенная скорость в момент времени ,
– мгновенная скорость в момент t2.
Слайд 4PS. Векторы скорости и
– касательные к траектории.
Очевидно:
При малых очевидно, что
.
Средняя скорость
Мгновенная скорость
PS. Другой вид математической записи («точка» обозначает производную по времени)
.
Средняя путевая скорость
– путь, пройденный за . При получаем:
Слайд 5
Мгновенная путевая скорость (при
):
Среднее ускорение за промежуток времени (t1, t2):
Мгновенное ускорение (в
момент t):
Очевидно:
PS.1. Если закон движения задан, например, известна зависимость , то мы имеем о движении полную информацию, и все величины, определённые равенствами (1.6) – (1.14) легко вычисляются, точно так же, как и их проекции на декартовы оси.
PS.2 Переход и выполняется с помощью дифференцирования.
,
выполняется с помощью интегрирования.
Чтобы найти по заданной , необходимо знать начальное значение
Аналогично:
Пример 1.
Пусть МТ движется с . Тогда можно найти
Интегрируя ещё раз, получаем закон движения:
Это равенства, связывающие кинематические величины в общем случае,
т.е. при произвольном движении МТ.
Пример 2. (из школьной жизни!). Прямолинейное равноускоренное движение.
Очевидно, что
Слайд 7Векторные равенства можно записать в проекциях на оси координат:
,
, (1.20а,б)
, , (1.21а,б)
, (1.22)
(1.23)
и т.д.
Слайд 81.2. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ НА ПЛОСКОСТИ.
УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ
ДВИЖЕНИИ: ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ.
Очевидно, при криволинейном движении ускорение материальной
точки отлично от нуля, т.к. вектор скорости изменяется по величине и по направлению.
Представим вектор скорости МТ в виде где
т.е. – единичный вектор, направленный по скорости
Продифференцируем уравнение :
Обозначим:
Слайд 9
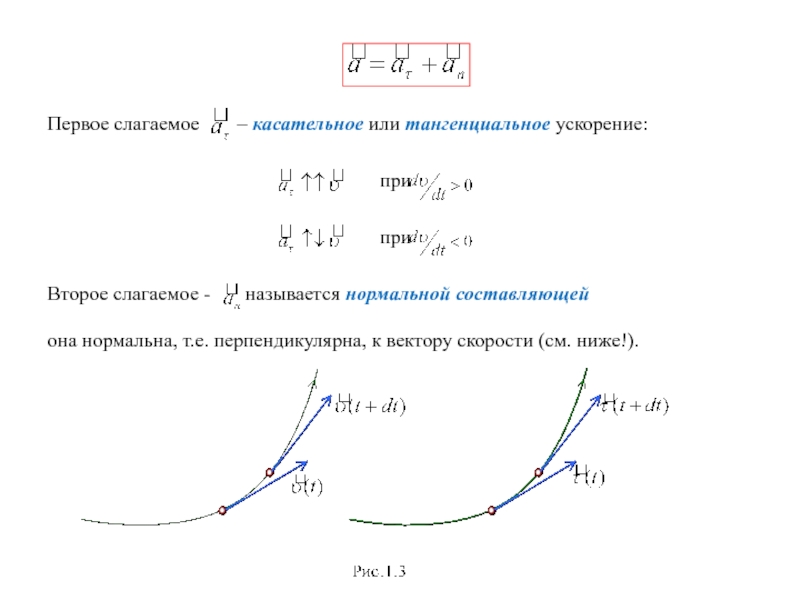
Первое слагаемое – касательное или тангенциальное ускорение:
при
при
Второе слагаемое - называется
нормальной составляющей
она нормальна, т.е. перпендикулярна, к вектору скорости (см. ниже!).
Рассматривая этот треугольник как бесконечно малый сектор, имеем
Но
. Отсюда
Слайд 11Если ввести бесконечно малый вектор поворота
, направление которого указано на рисунке 1.4 – «к нам»,
– то будем иметь с учётом (1.31) и (1.33):
(1.34)
Таким образом, (см. (1.31), (1.28)),
(1.35)
Следовательно, равенство (1.29) – разложение вектора ускорения на две взаимно перпендикулярные составляющие.
Далее, можно представить в виде
(1.36)
Направления , , в случае показаны на рисунке 1.5.
Слайд 12 Если считать малый отрезок криволинейной траектории частью окружности, то величина
(1.37)
называется вектором угловой скорости.
Вектор определяет как
направление поворота, так и величину угла поворота радиуса-вектора за единицу времени.
Направление движения МТ по окружности и направление связаны правилом буравчика.
Слайд 131.3 НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ.
СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ. РАДИУС КРИВИЗНЫ ПЛОСКОЙ ТРАЕКТОРИИ.
PS.
.
При движении против часовой стрелки направлена «к нам»
по часовой – «от нас»
За время dt радиус-вектор изменится на :
Используя аналогию треугольников:
Слайд 14Дифференцируя, находим ускорение:
Второе слагаемое есть нормальное ускорение:
Тогда первое, очевидно, равно
:
Введём новое определение: угловым ускорением МТ назовём величину
Поделив обе части
на , будем иметь
Слайд 15Теперь ускорение:
Двойное векторное произведение вычислим по известной математической формуле
,
что даёт
Учитывая, что ,
получаем:
Таким образом, в разложении:
слагаемые имеют вид:
Нормальная составляющая ускорения – это хорошо известное из школьного курса центростремительное ускорение.
Ускорение материальной точки , движущейся по окружности, называют также полным ускорением.
Слайд 16 Рассмотрим аналогию между ускоренными прямолинейным и криволинейным движениями (на примере
МТ, движущейся по окружности)
Ось OZ направлена «к нам», –
единичный вектор, указывающий направление отсчёта положительных углов, которое связано с направлением OZ правилом буравчика
Для движения вдоль оси OX имеем
Слайд 17Для движения по окружности:
Равнопеременное движение вдоль оси описывается равенствами:
Равнопеременное
движение по окружности:
где – угловое перемещение
материальной точки
Слайд 18Таблица соответствия линейных и угловых величин
линейные
угловые
Уравнения, связывающие линейные и угловые
переменные, характеризующие движение МТ по окружности
:
, ; (1.55а, б)
, , ; (1.56а, б, в)
, , ; (1.57а, б, в)
Здесь – проекции скорости и ускорения на вектор ,
; (1.58 а, б)
, . (1.59 а, б)
Малую окрестность точки плоской криволинейной траектории материальной точки можно рассматривать как малую дугу некоторой окружности. Радиус этой окружности – радиус кривизны траектории в окрестности данной точки, . Эта величина удовлетворяет равенству аналогичному (1.59 б).
. (1.60)