Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интерференция света
Содержание
- 1. Интерференция света
- 2. При наложении волн каждая из них входит
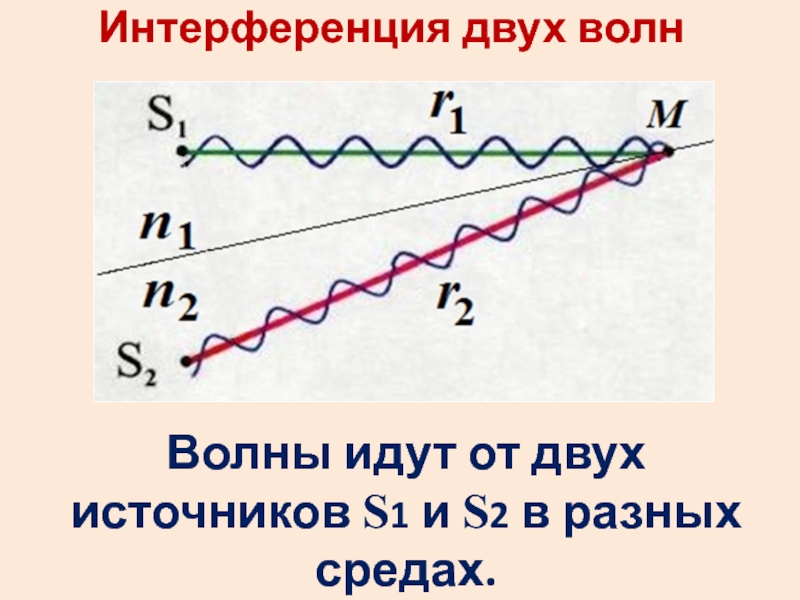
- 3. Интерференция двух волнВолны идут от двух источников S1 и S2 в разных средах.
- 4. Пусть обе волны монохроматические – одной частоты
- 5. В точке М надо сложить два колебания
- 6. По теореме косинусов амплитуда результирующего колебанияИнтенсивность результирующего колебанияИнтерференционное слагаемое
- 7. Это слагаемое может быть и >0 и
- 8. Интерференция заключается в перераспределении интенсивности волны между
- 9. В результате интерференции в одних точках пространства
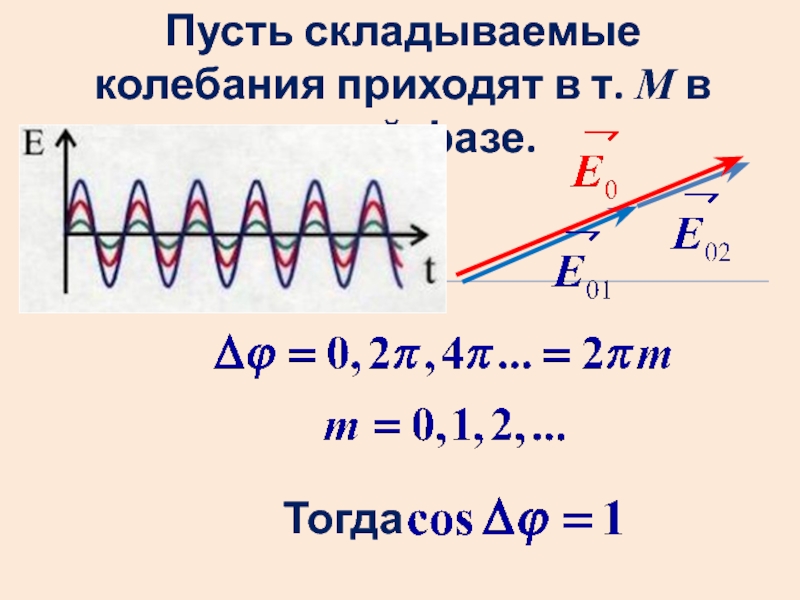
- 10. Пусть складываемые колебания приходят в т. М в одной фазе.Тогда
- 11. ПриИнтенсивность в точке МЭто интерференционный максимум.Интенсивность в
- 12. Пусть складываемые колебания приходят в т. М в противофазе.Тогда
- 13. ПриИнтенсивность в точке МЭто интерференционный минимум.
- 14. МинимумМаксимум
- 15. Условия максимума и минимума при интерференции.Пусть начальная фаза колебаний одинакова.Распишем разность фаз в т. М:
- 16. В скобках стоит разность оптических путей волн.Она называется оптической разностью хода волн Δ.
- 17. Условие максимума:Для максимума колебания должны быть в
- 18. Условие минимума:Для минимума колебания должны быть в
- 19. Целое число m называют порядком интерференционного максимума или минимума.
- 20. Виды интерференционных картин
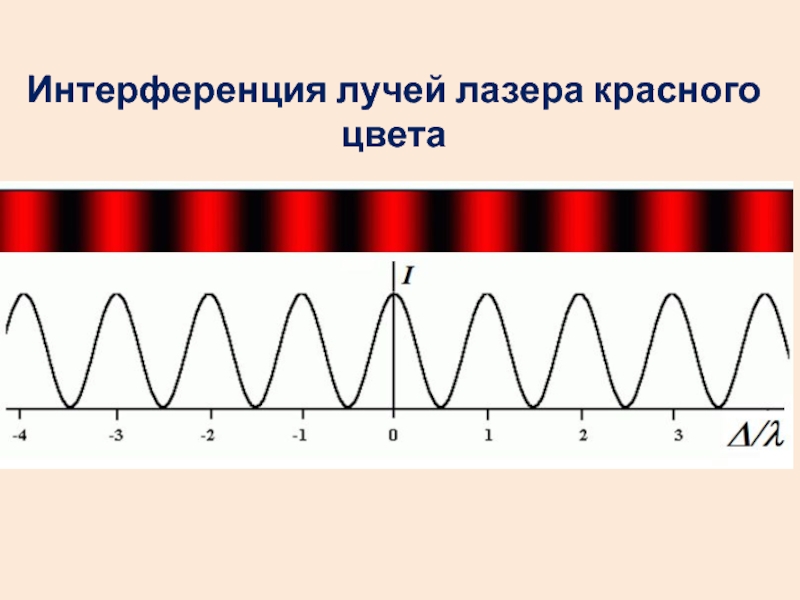
- 21. Интерференция лучей лазера красного цвета
- 22. КогерентностьДва разных источника никогда не могут испускать
- 23. Причина пространственных наруше-ний когерентности – неточечность реального источника волн. Разные атомы, составляющие источник, излучают несогласованно.
- 24. Причина временных нарушений – дискретность излучений атомов.
- 25. Получить когерентные источники можно только разделяя один
- 26. Такой опыт впервые осуществил Томас Юнг.
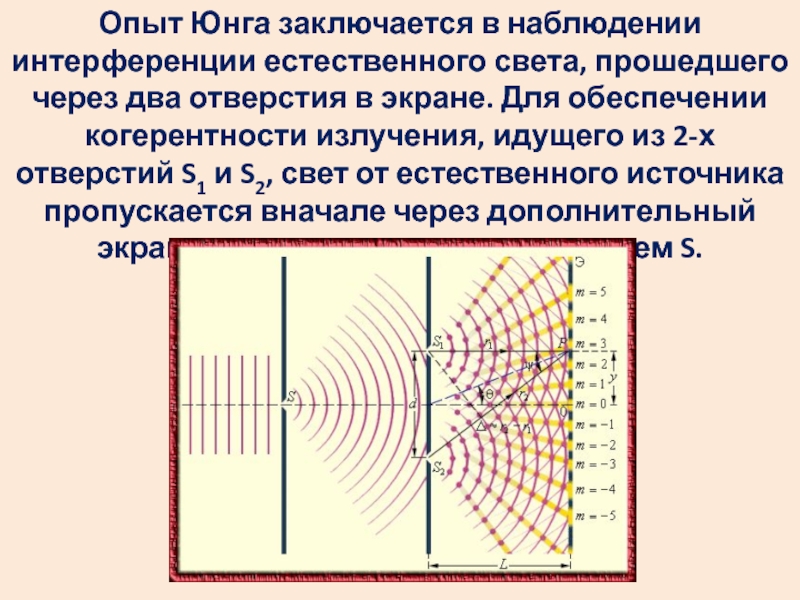
- 27. Опыт Юнга заключается в наблюдении интерференции естественного
- 28. Схема опыта ЮнгаФиолетовый и красный треу-гольники подобны, значит:
- 29. Запишем это для двух соседних максимумов с номерами m и m+1.
- 30. Получили формулу для ширины интерференционной полосы:По ней можно найти d.
- 31. Другие способы получения когерентных источников.Зеркала Френеля
- 32. Бипризма Френеля
- 33. ИнтерферометрыИнтерферометры – это оптические приборы, использующие законы интерференции света, проходящего через исследуемые вещества.
- 34. Интерференция светаИнтерферометр ЖаменаSWF-Модель «Интерферометр Жамена»WMV-Видео «Интерферометр Жамена»
- 35. Интерференция светаИнтерферометр РэлеяSWF-Модель «Интерферометр Рэлея»WMV-Видео «Интерферометр Рэлея»
- 36. Интерференция светаИнтерферометр МайкельсонаМодель интерферометра Майкельсона
- 37. Интерференция светаИнтерференционная картина в опыте Майкельсона с источником света лампой накаливания
- 38. Интерференция светаИнтерферометр Майкельсона (видеоклип)
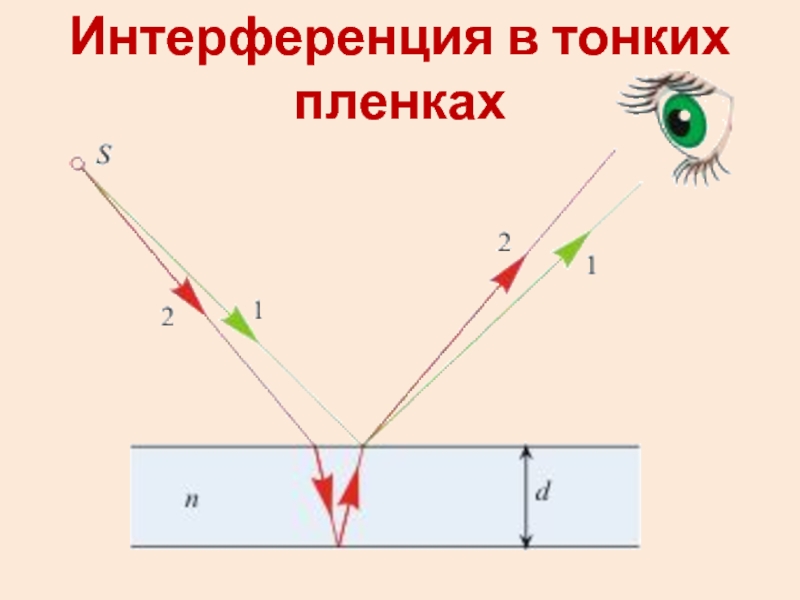
- 39. Интерференция в тонких пленках
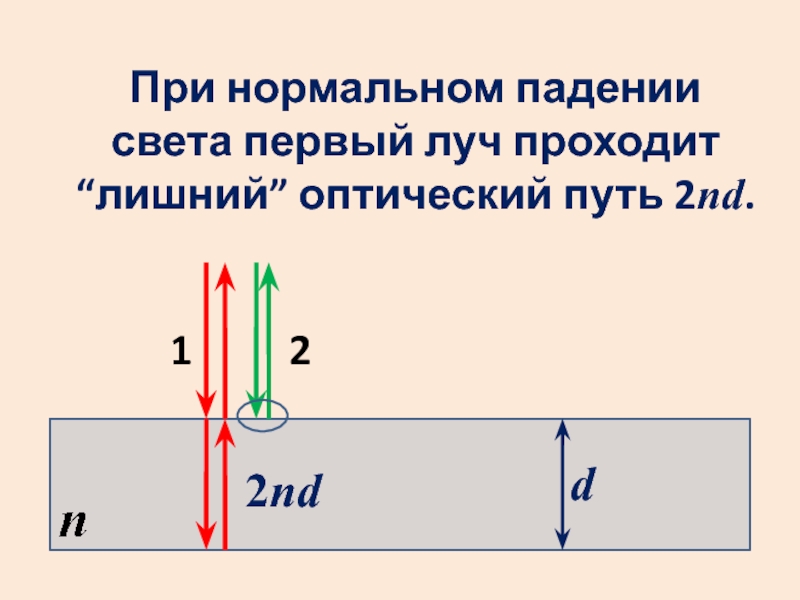
- 40. dПри нормальном падении света первый луч проходит “лишний” оптический путь 2nd. 2nd12
- 41. При отражении света от оптически более плотной
- 42. Оптическая разность хода лучей на рисунке :
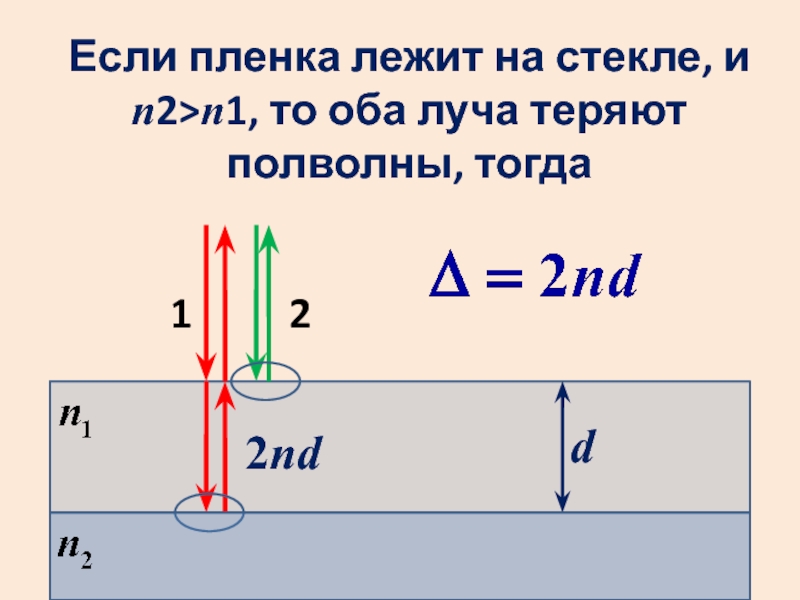
- 43. dЕсли пленка лежит на стекле, и n2>n1, то оба луча теряют полволны, тогда 2nd12
- 44. d2nd12В проходящем свете лучи не отражаются от оптически более плотной среды, и
- 45. Лучи усиливают друг друга, когда и гасят, когда
- 46. Так как Δ при отражении и прохождении
- 47. d12При падении луча под углом α:в отраженном светев проходящем свете
- 48. Рассеянный свет падает и отражается под разными
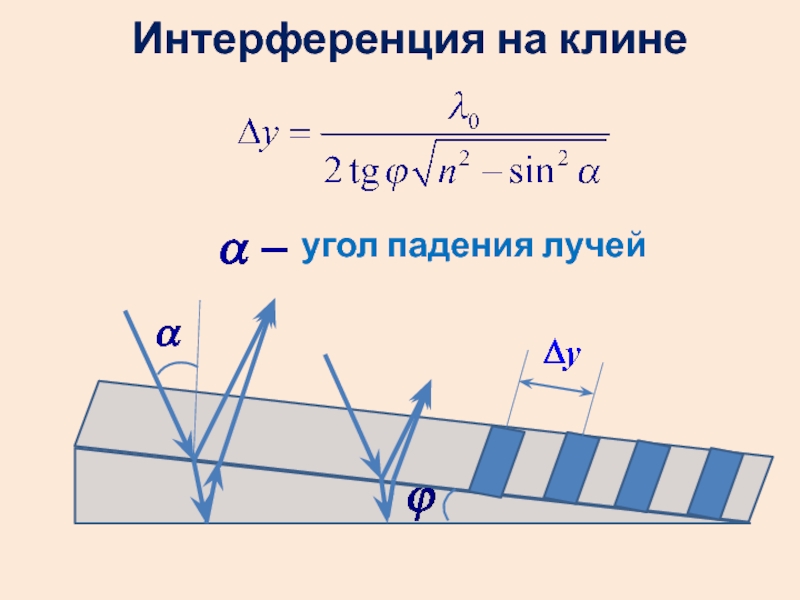
- 49. Интерференция на клинеугол падения лучей
- 50. Полосы, образующиеся при интерферен-ции на клине, называются полосами равной толщины.
- 51. Мыльный пузырь
- 52. Слайд 52
- 53. Интерференция света
- 54. Кольца Ньютона –- пример полос равной толщины
- 55. m = 1, 2, 3,…. – номер кольцаОптическая разность хода лучей:длина волны в веществе клина
- 56. Наблюдения в микроскопДля белого света кольца
- 57. Интерференция светаМодель колец Ньютона
- 58. Кольца Ньютона (видеоклип)
- 59. Применение интерференцииИзмерение длин волн.Измерение расстояний.Измерение показателя преломления.Просветление
- 60. Скачать презентанцию
При наложении волн каждая из них входит в результирующую волну независимо друг от друга. Принцип суперпозиции волн
Слайды и текст этой презентации
Слайд 4Пусть обе волны монохроматические – одной частоты ω.
И пусть
световой вектор в точке М направлен вдоль одной и той
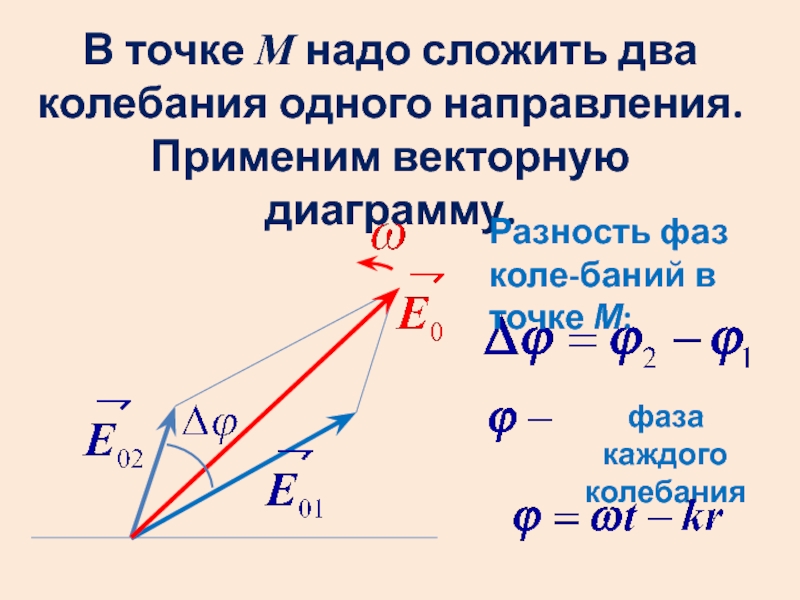
же линии для обеих волн.
Слайд 5В точке М надо сложить два колебания одного направления. Применим
векторную диаграмму.
Разность фаз коле-баний в точке М:
фаза каждого колебания
Слайд 6По теореме косинусов амплитуда результирующего колебания
Интенсивность результирующего колебания
Интерференционное слагаемое
Слайд 7Это слагаемое может быть и >0 и
от разности фаз.
Если она все время изменяется (например, ω1 ≠ω2),
то среднее по времени значение косинуса дает нуль. Тогда простоНет никакой интерференции.
Слайд 8Интерференция заключается в перераспределении интенсивности волны между точками пространства.
Она
возникает только при наложении когерентных волн.
Когерентные волны имеют в
данной точке постоянную разность фаз.Это возможно, только если частоты колебаний одинаковы (ω1=ω2).
Слайд 9В результате интерференции в одних точках пространства будут наблюдаться максимумы
интенсивности. В этих точках волны усиливают друг друга. В других
точках будут наблюдаться минимумы интенсивности. Там волны гасят друг друга. Для световых волн это выглядит как светлые и темные пятна.
Слайд 11При
Интенсивность в точке М
Это интерференционный максимум.
Интенсивность в точке максимума в
4 раза больше, чем у каждой волны.
Слайд 15Условия максимума и минимума при интерференции.
Пусть начальная фаза колебаний одинакова.
Распишем
разность фаз в т. М:
Слайд 16В скобках стоит разность оптических путей волн.
Она называется оптической разностью
хода волн Δ.
Слайд 17Условие максимума:
Для максимума колебания должны быть в одной фазе: Δϕ
= 2πm, m = 0,1,2…
Если оптическая разность хода равна
целому числу длин волн, то в данной точке будет интерференционный максимум.
Слайд 18Условие минимума:
Для минимума колебания должны быть в противофазе: Δϕ =
π(2m+1), m = 0,1,2…
Если оптическая разность хода равна полуцелому
числу длин волн, то в данной точке будет интерференционный минимум.
Слайд 22Когерентность
Два разных источника никогда не могут испускать когерентные волны. Даже
волна, испускаемая одним источником, может быть некогерентна самой себе.
Есть
два типа нарушения когерентности – пространственное и временное.
Слайд 23Причина пространственных наруше-ний когерентности – неточечность реального источника волн. Разные
атомы, составляющие источник, излучают несогласованно.
Слайд 24Причина временных нарушений – дискретность излучений атомов. Атомы излучают не
непрерывно, а цугами.
Из-за этого фаза волны изменяется скачками.
Слайд 25Получить когерентные источники можно только разделяя один и тот же
пучок света на разные лучи. Пучок должен быть очень узким
(пространственно когерентным). Разность хода не должна быть большой, чтобы складывались колебания из одного и того же цуга.
Слайд 27Опыт Юнга заключается в наблюдении интерференции естественного света, прошедшего через
два отверстия в экране. Для обеспечении когерентности излучения, идущего из
2-х отверстий S1 и S2, свет от естественного источника пропускается вначале через дополнительный экран с очень маленьким отверстием S.
Слайд 33 Интерферометры
Интерферометры – это оптические приборы, использующие законы интерференции света,
проходящего через исследуемые вещества.
Слайд 34Интерференция света
Интерферометр Жамена
SWF-Модель «Интерферометр Жамена»
WMV-Видео «Интерферометр Жамена»
Слайд 35Интерференция света
Интерферометр Рэлея
SWF-Модель «Интерферометр Рэлея»
WMV-Видео «Интерферометр Рэлея»
Слайд 37Интерференция света
Интерференционная картина в опыте Майкельсона с источником света лампой
накаливания
Слайд 41При отражении света от оптически более плотной среды фаза волны
скачком изменяется на π радиан. Это соответствует изменению оптической разности
хода на полволны. Говорят, что луч “теряет” полволны. На рисунке это делает луч 2.
Слайд 46Так как Δ при отражении и прохождении света отличается на
λ/2, то максимуму на отражение соответствует минимум на прохождение и
наоборот.
Слайд 48Рассеянный свет падает и отражается под разными углами. Для каких-то
углов могут выполниться условия минимума, для других – условия максимума.
В результате будут наблюдаться темные и светлые кольца. Эти кольца называют полосами равного наклона. Каждое кольцо образуется лучами, падающими на пленку под одинаковым углом с разных направлений. Если свет белый, кольца будут радужными.
Слайд 54Кольца Ньютона –
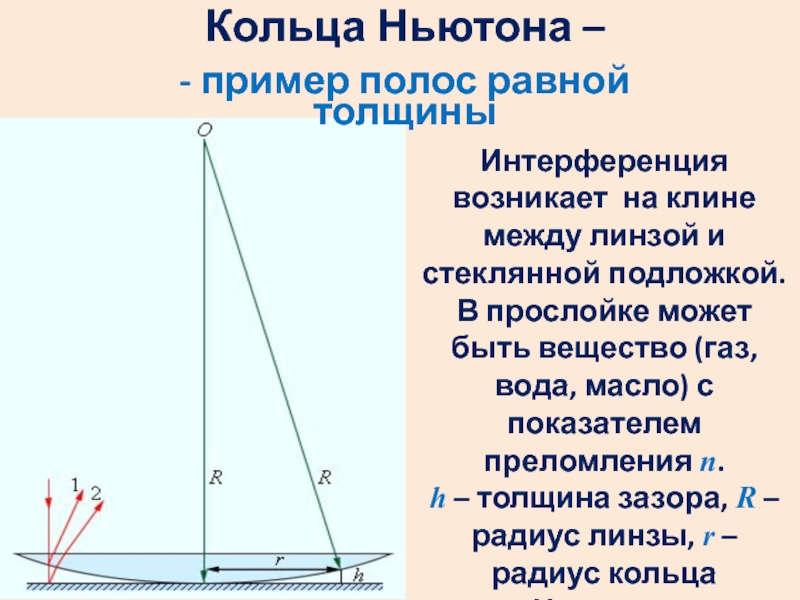
- пример полос равной толщины
Интерференция возникает на
клине между линзой и стеклянной подложкой. В прослойке может быть
вещество (газ,вода, масло) с показателем преломления n.h – толщина зазора, R – радиус линзы, r – радиус кольца Ньютона.
Слайд 56
Наблюдения в микроскоп
Для белого света кольца будут радужными.
В отраженном свете
в центре картины – темное пятно (разность хода лучей λ/2),
в проходящем свете – светлое пятно.
Слайд 59Применение интерференции
Измерение длин волн.
Измерение расстояний.
Измерение показателя преломления.
Просветление оптики.
Линзу оптического прибора
покрывают пленкой, такой чтобы выполнялось условие минимума на отражение. Тогда
весь свет проходит внутрь.
