Лекция 4

массы. Формула Циолковского.

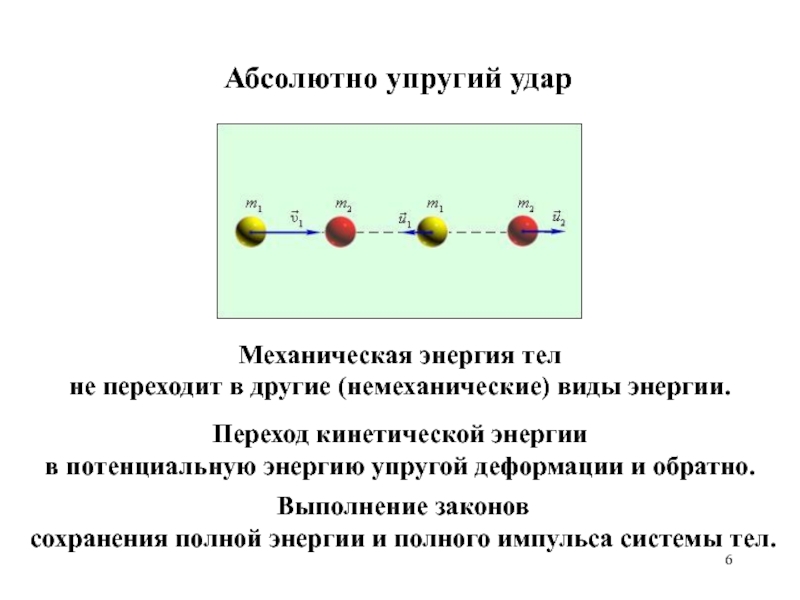
Механическая энергия

Сила, работа и потенциальная энергия, связь между

кинетической и потенциальной энергий,
г) как кинетическая, так и потенциальная энергии.
Закон

в)

движения: угловая скорость и угловое ускорение, их связь с линейной

неупругий удары.

энергии.
Переход кинетической энергии
в потенциальную энергию упругой деформации и обратно.
Выполнение

энергии во внутреннюю энергию.
После удара:
движение тел с одинаковой скоростью

суммарной энергии различных видов - механической и внутренней.
Абсолютно неупругий удар

удар

движение по концентрическим окружностям.

оси.
Неоднозначность в выборе направления поворота
– поворот возможен по или

угловой скорости

обращения Т при равномерном вращении – время, за которое тело

вокруг точки, относительно которой он берется.
Возможность произвольного вращения тела
относительно точки

Момент силы относительно оси

плоскости,
в которой лежат сила F и точка О,
т.е.

Момент силы относительно оси

тело вокруг этой оси.
Момент силы относительно оси

силы, не действующие вдоль одной прямой.
Плечо пары сил –
расстояние

выбора точки О.

которой лежат силы.
Численное значение вектора момента пары сил – произведение

же прямой.
Равенство по модулю и противоположное направление вдоль одной и

неизменным расстоянием между ними.
Момент инерции тела равен
сумме моментов инерции его

IC относительно оси, параллельной данной и проходящей через центр масс

оси С.
Оси перпендикулярны плоскости экрана.
а – расстояние между осями.

энергия i-й элементарной массы
Кинетическая энергия тела
вращающегося вокруг неподвижной оси

соотносятся как:
а) p1 < p2,
б) p1 = p2,
в)