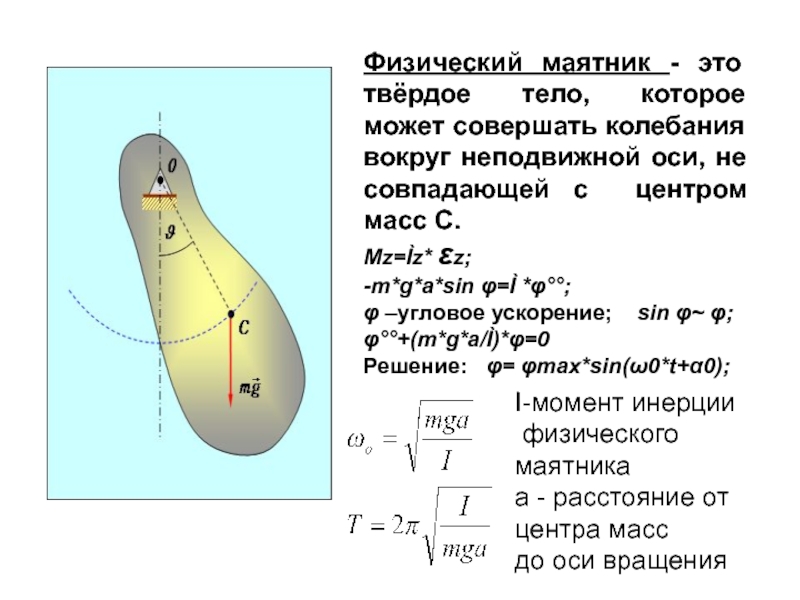
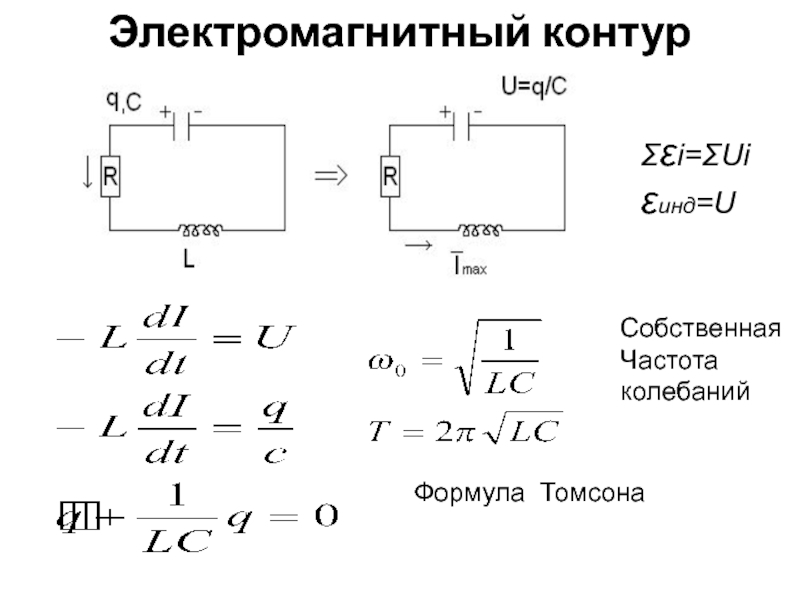
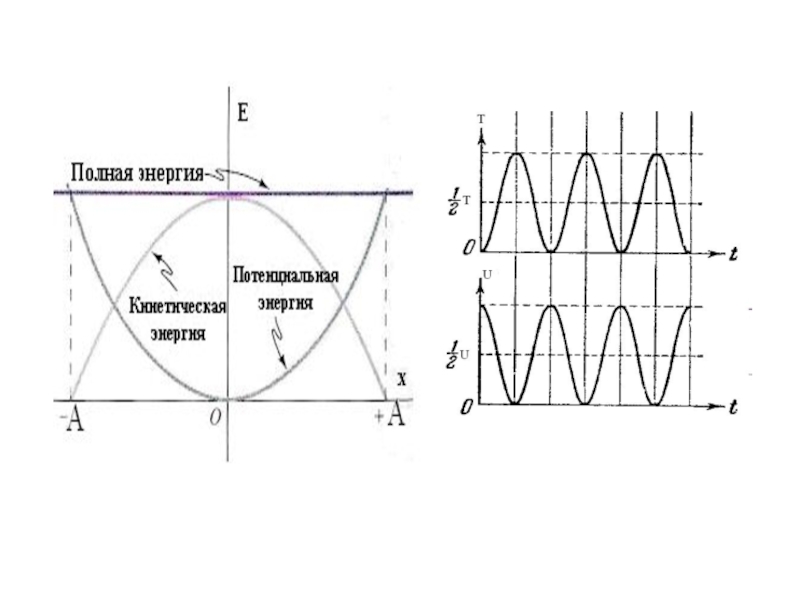
повторяемости во времени.
Осциллятор – это система, совершающая колебания.
Если состояние системы
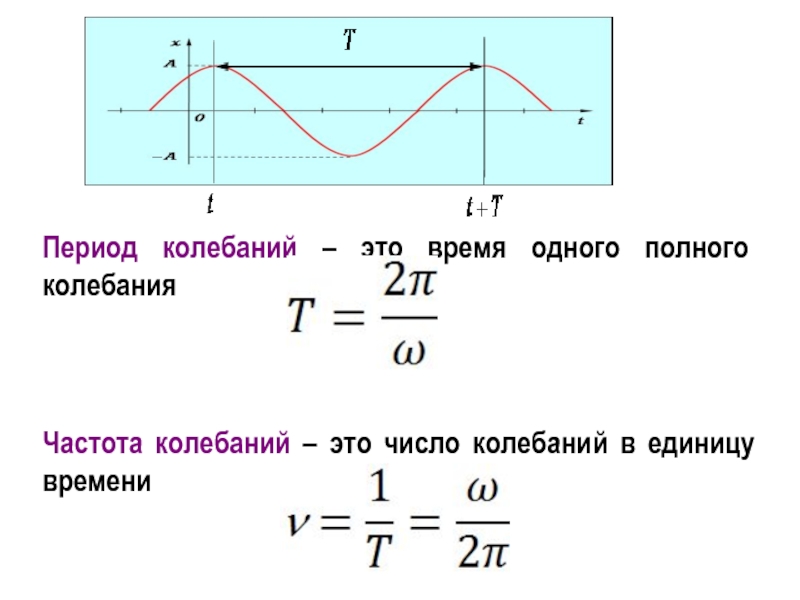
или значение какой-либо физической величины повторяется через равные промежутки времени, то такие колебания называются периодическими.f(t)=f (t+T) T – период {с}












![Колебания Математический маятник M=Ì* ε; M –момент силы; M=[R*F];Ì –момент инерции; ε -угловое ускорение; Математический маятник M=Ì* ε; M –момент силы; M=[R*F];Ì –момент инерции; ε -угловое ускорение;](/img/thumbs/713eb45001544e7811415da6ba4f8009-800x.jpg)