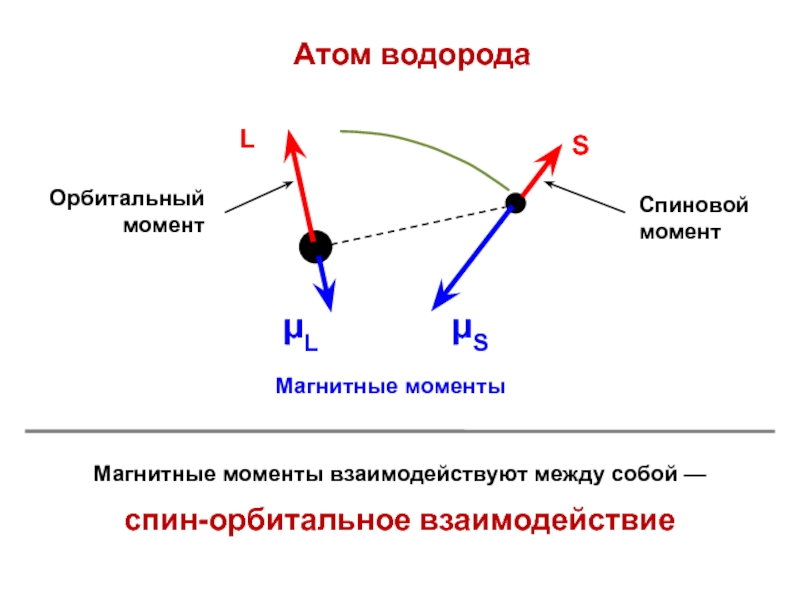
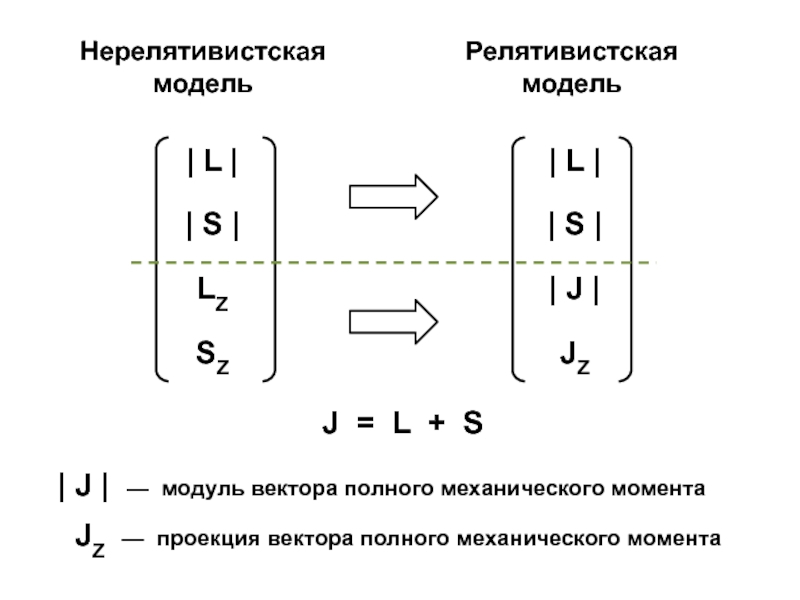
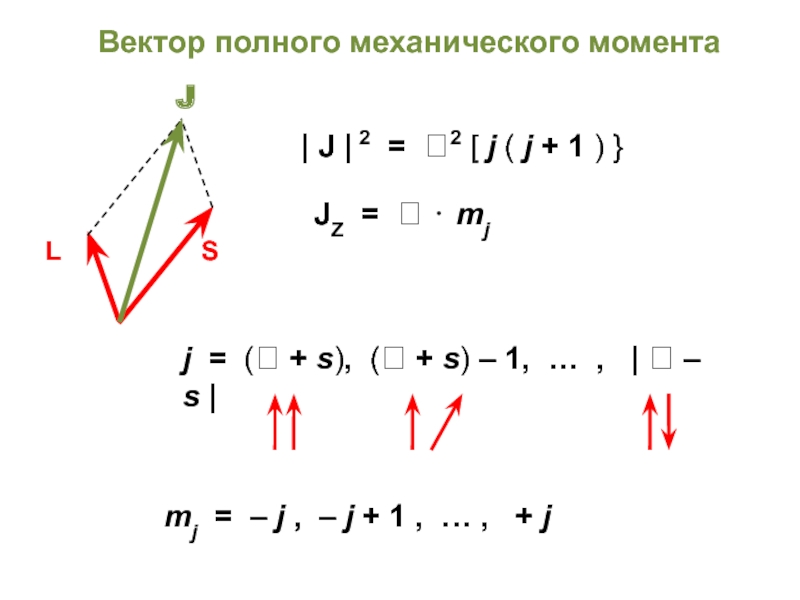
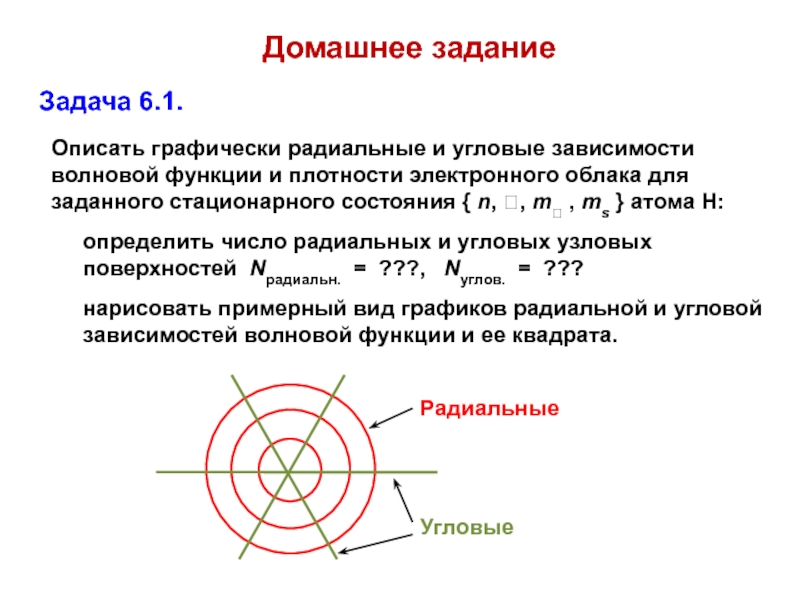
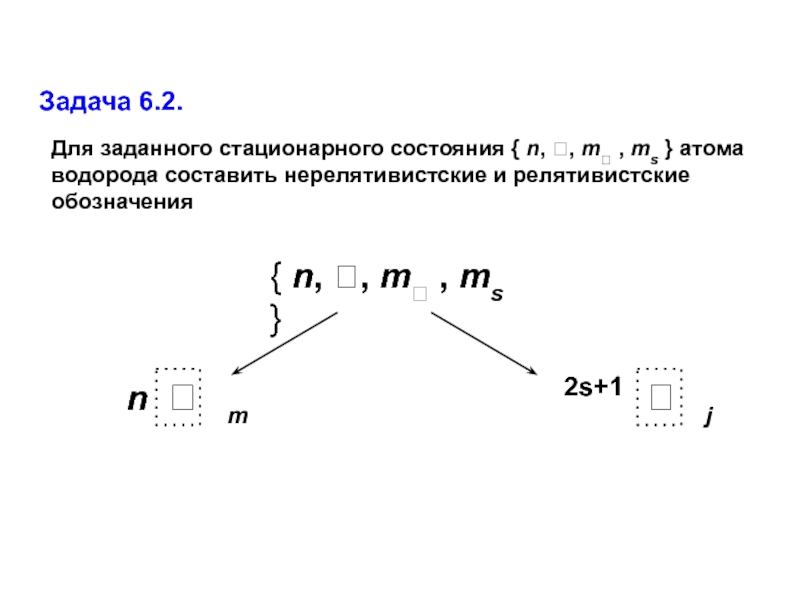
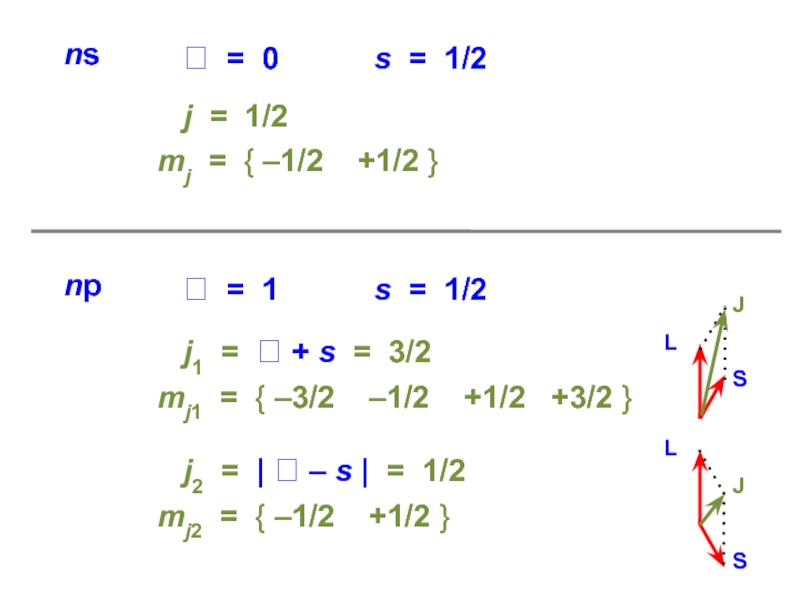атом водорода — это единственная реальная система, для которой возможно
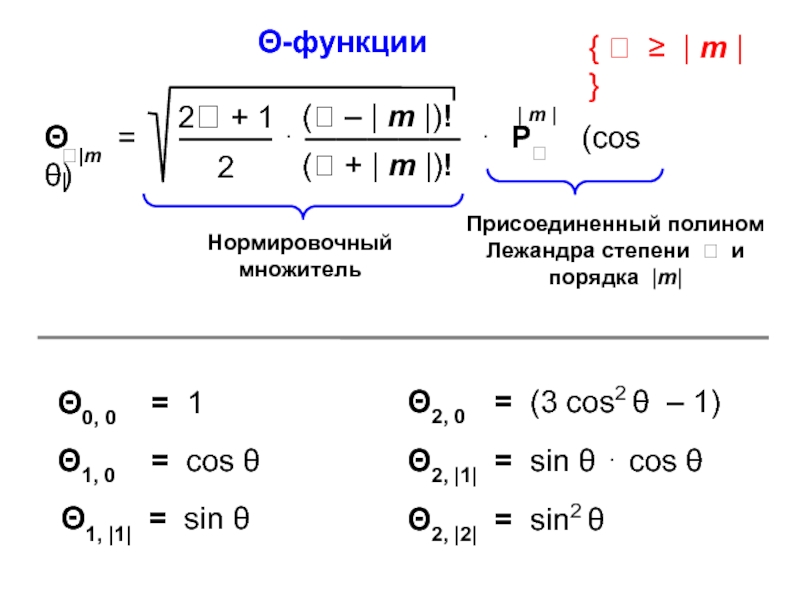
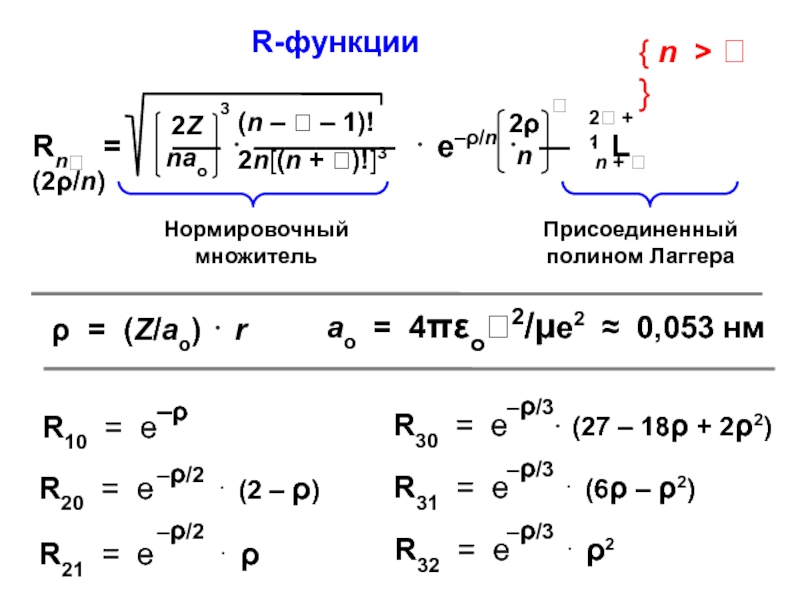
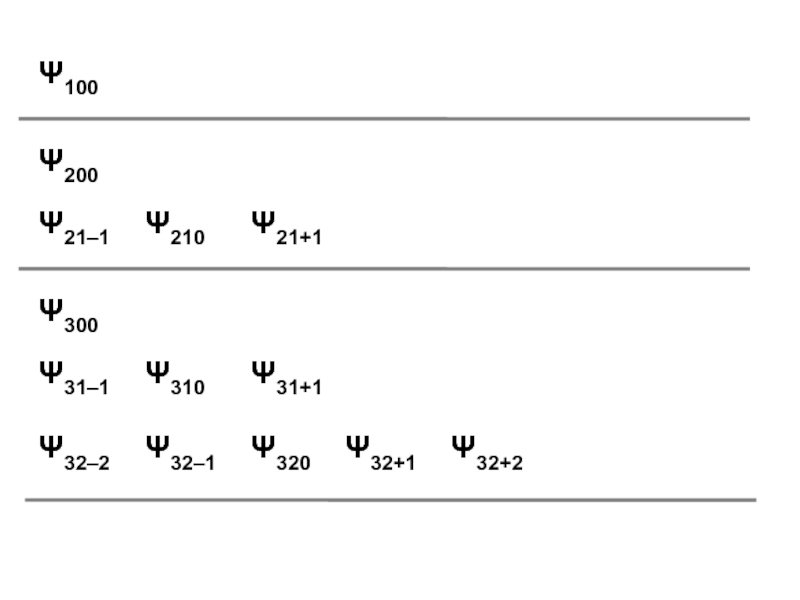
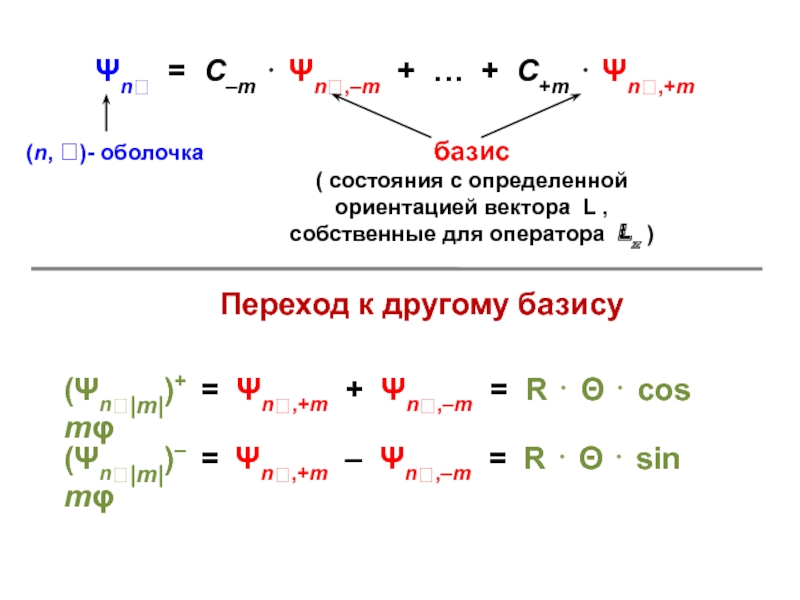
установить аналитический вид волновых функций2) волновые функции стационарных состояний атома водорода образуют базисный набор, который можно использовать для анализа волновых функций более сложных систем — многоэлектронных атомов и молекул
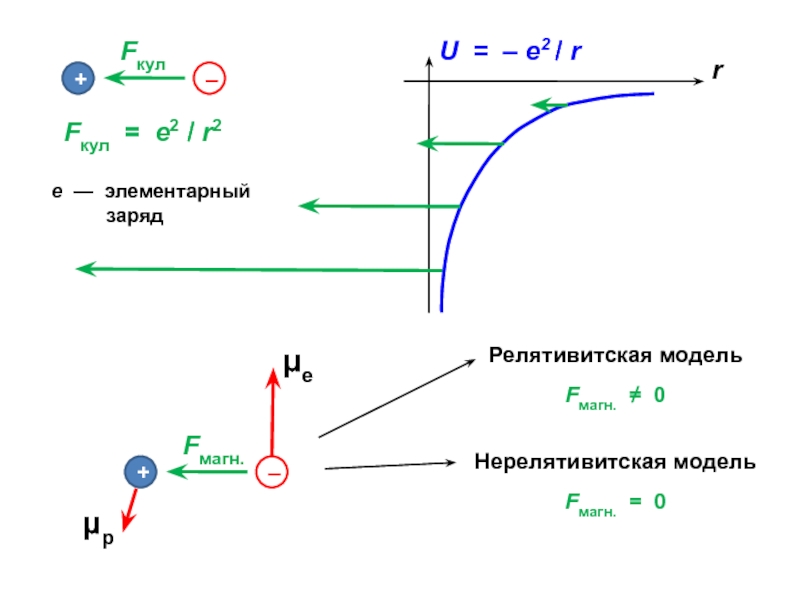
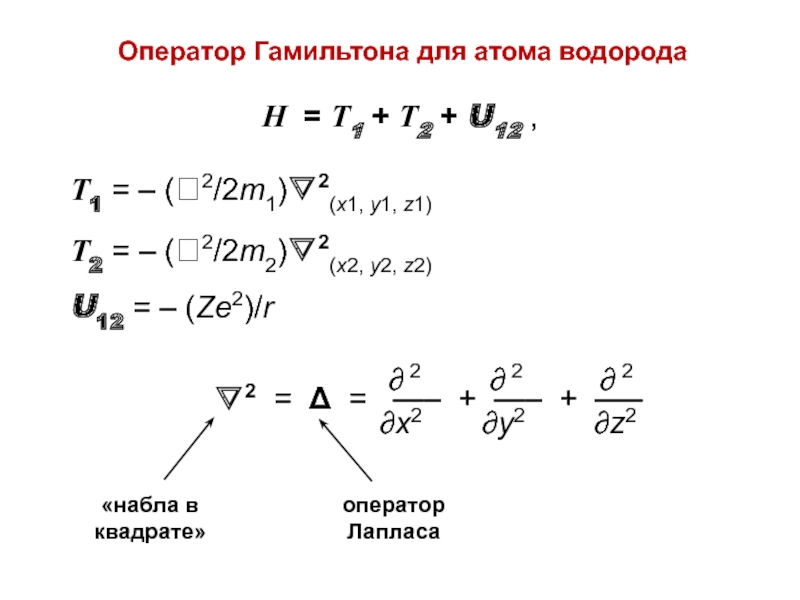
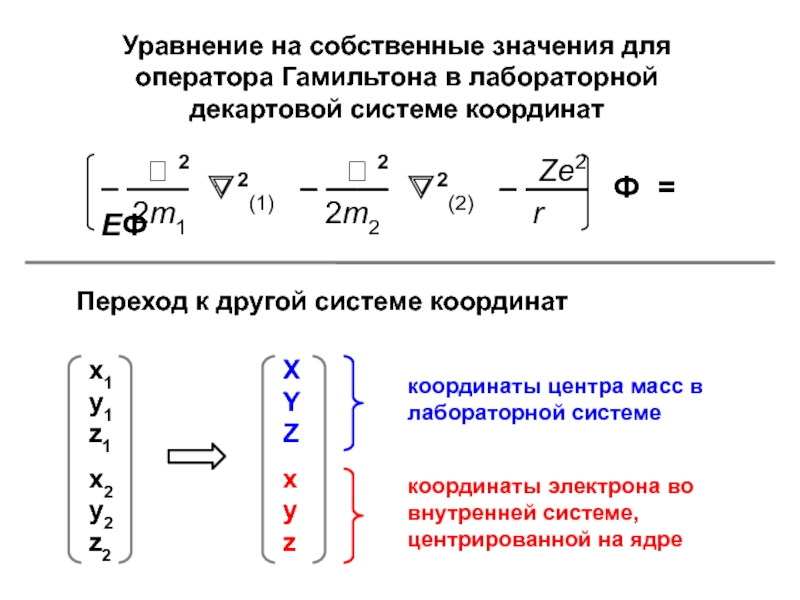
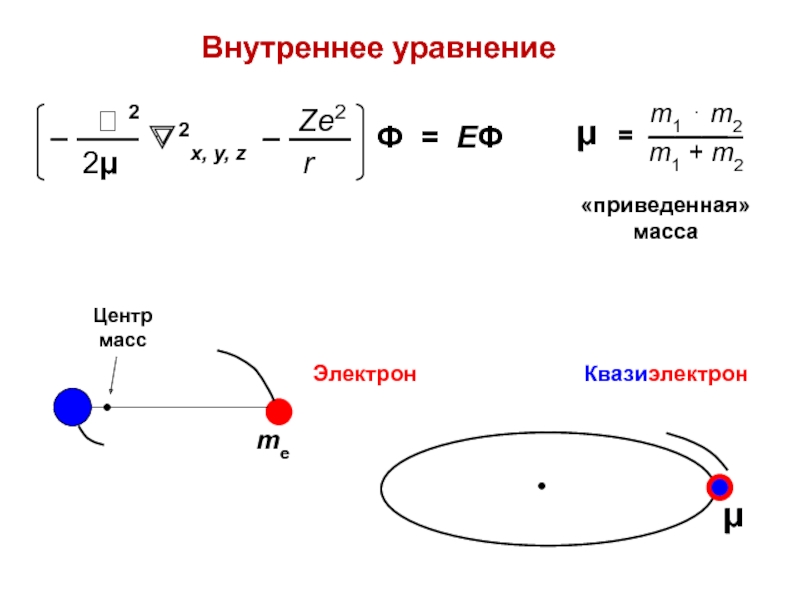
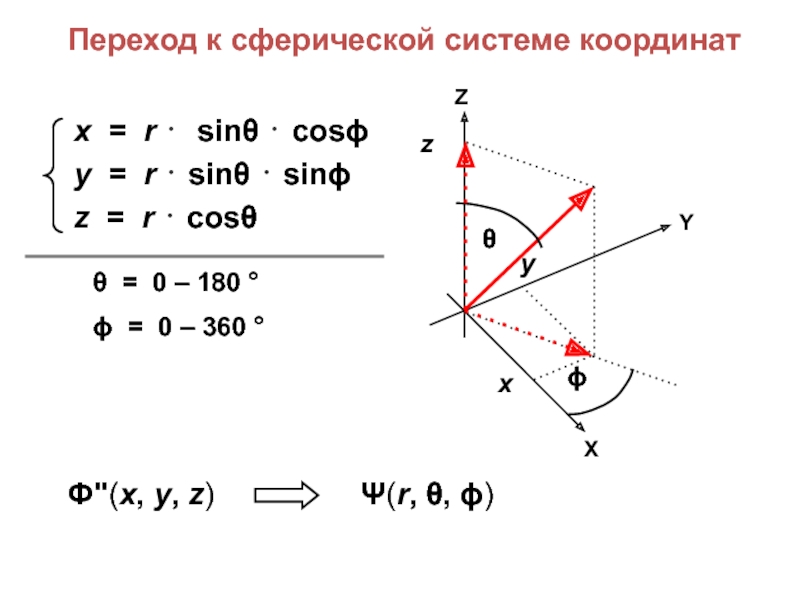
Водородоподобные атомы
(ядро + 1 электрон)
He+ Li2+ Be3+ …


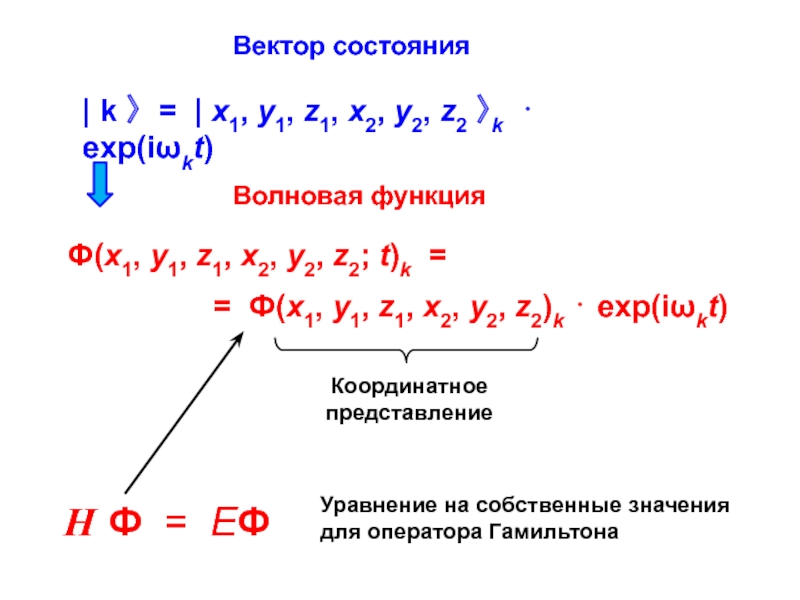












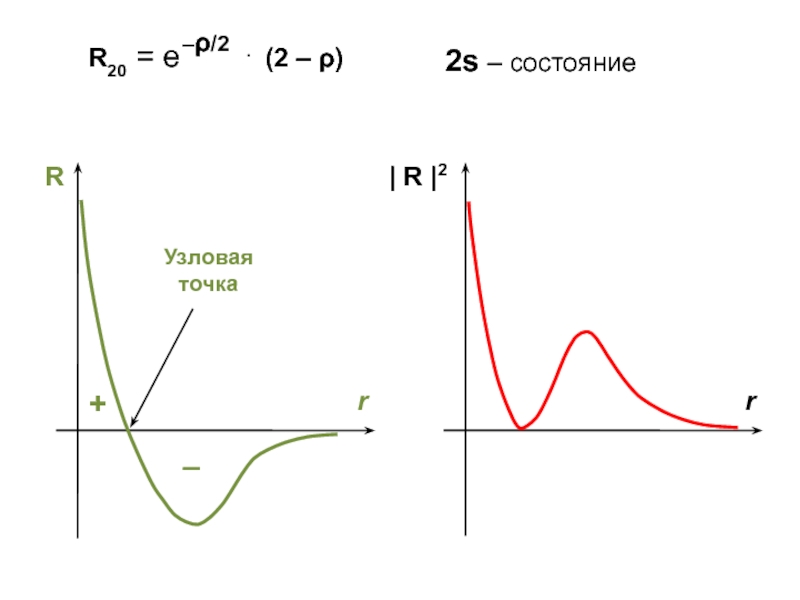
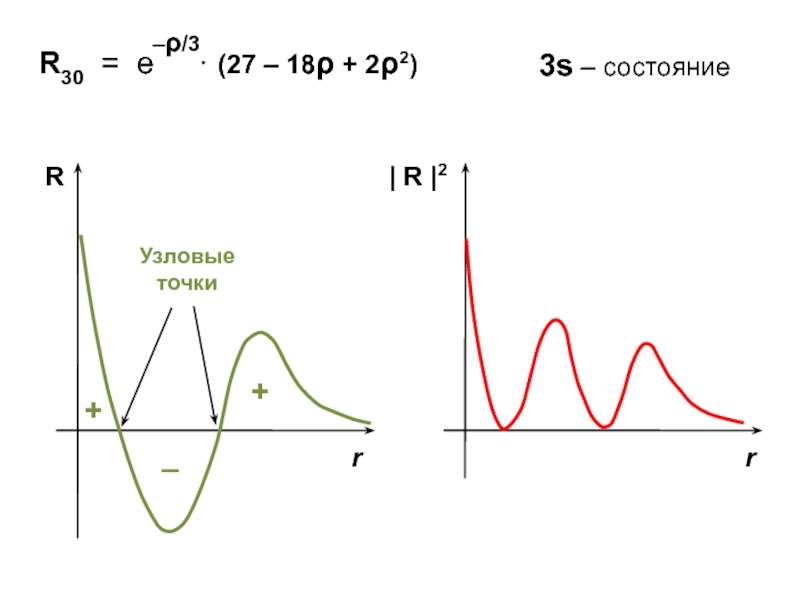
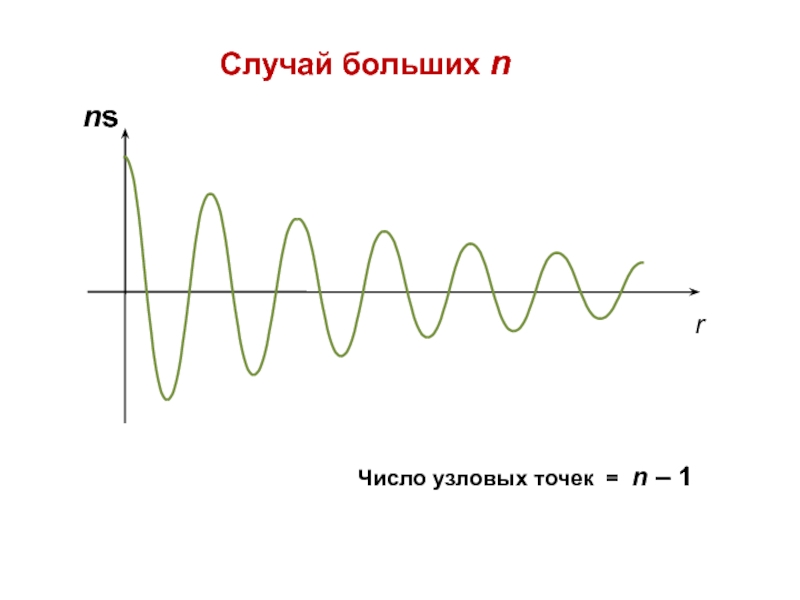
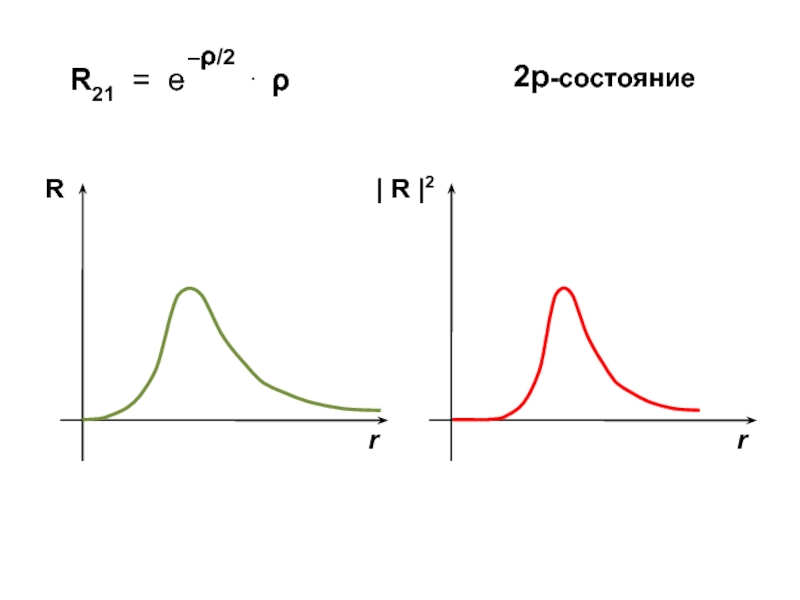
![Атом водорода Спиновые характеристики электрона Модуль | S |2 = 2 [ Спиновые характеристики электрона Модуль | S |2 = 2 [ s (s + 1) ]](/img/thumbs/f1190c6c4d0a8c8d500b70ae849c13fa-800x.jpg)