20.04.20 Определение производной, ее геометрический и физический

(1)

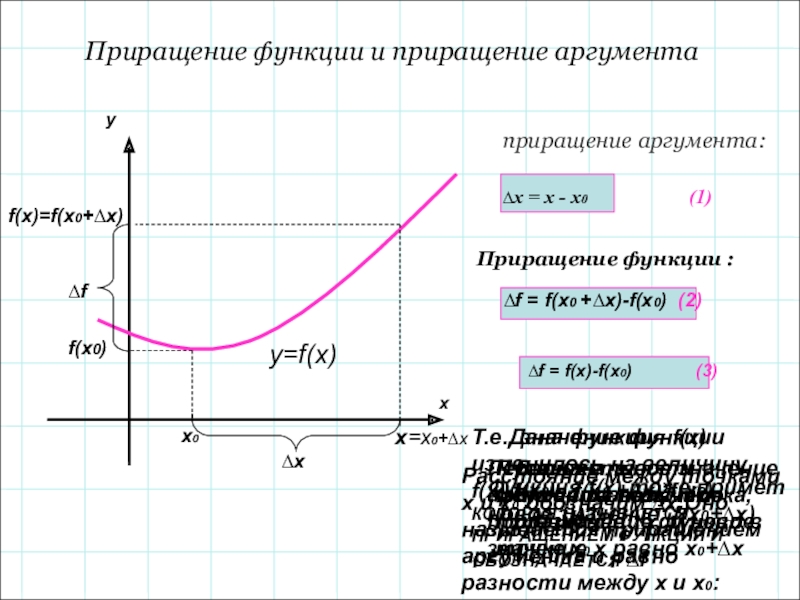
Приращение функции :

∆f = f(x0 +∆x)-f(x0) (2)

∆f = f(x)-f(x0) (3)

x

В окрестности точки х0 возьмём точку х

Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0

Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:

Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х

Функция f(х) тоже примет новое значение: f(x0+∆x)

Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f

Дана функция f(x)

начало отсчета, единица измерения и направление, движется некоторое тело.
Закон

движения задан формулой s=s (t), где t — время, s (t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета.
Найти скорость движения тела в момент времени t.

М
пройдя путь от начала движения ОМ = s{t). Дадим

аргументу t
приращение ∆t и рассмотрим момент времени t+∆t Координата
материальной точки стала другой, тело в этот момент будет
находиться в точке P : OP=s(t+∆t) Значит, за ∆t секунд тело переместилось из точки М в точку Р, т.е. прошло путь МР. Имеем:
MP=OP-OM=s(t+∆t)-s(t)=∆s Полученную разность мы назвали приращением функции
Путь ∆s тело прошло за ∆t секунд.
Нетрудно найти среднюю скорость движения тела за промежуток времени [t;t+∆t] :
=

А что такое скорость v (t) в момент времени t (ее называют иногда
мгновенной скоростью)? Можно сказать так: это средняя скорость движения
за промежуток времени [t;t+∆t] при условии , что ∆t выбирается все меньше и
меньше; точнее: иными словами, при условии, что ∆t→0.Это значит , что

Подводя итог решению задачи 1, получаем:

к графику функции стр.158

х0 называется предел отношения приращения функции к приращению аргумента при

последнем стремящимся к нулю:

в новую точку х + ∆х, найти f(x +

∆х).
Найти приращение функции: ∆f = f(x + ∆х) – f(x).
Составить отношение .
Вычислить lim .
Этот предел и есть f ′(x).

Алгоритм нахождения производной

∆x = x – x0
2)

∆f = f(x+x0) – f(x0)
3)

4)

k – угловой коэффициент прямой(секущей)
А
В
Итог
Геометрический смысл

производной
Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Автоматический показ.

=
Мгновенная скорость
или
Скорость изменения функции

Значение производной в точке

=

§27, 27.1(в)-27.5(в).