Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
29.04.20. Гомотетия. Подобие фигур
Содержание
- 1. 29.04.20. Гомотетия. Подобие фигур
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
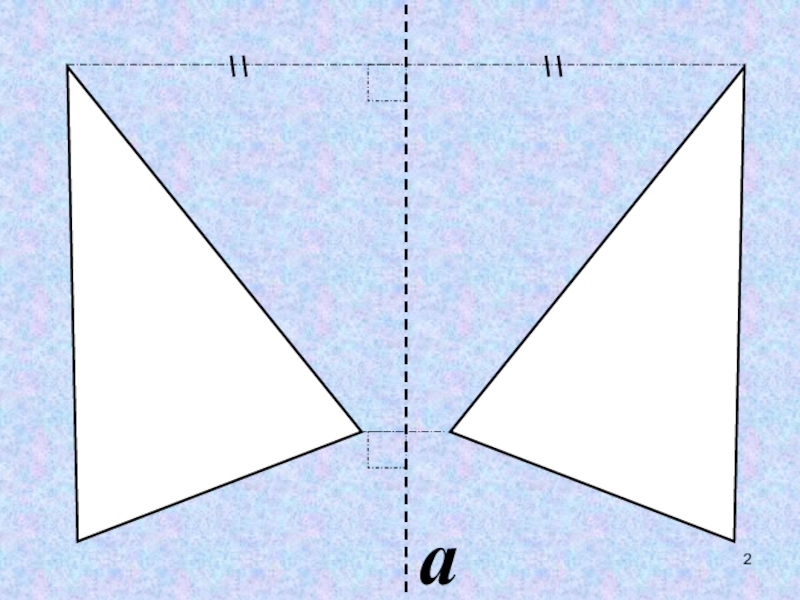
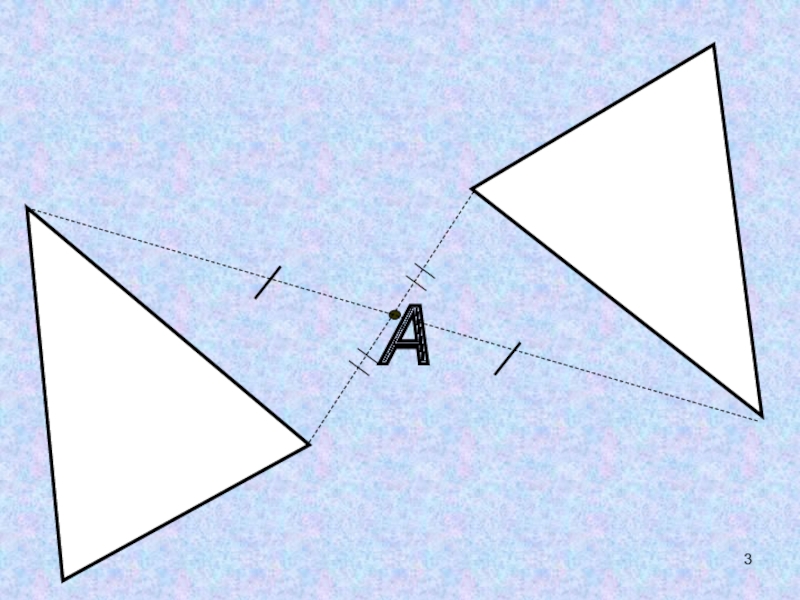
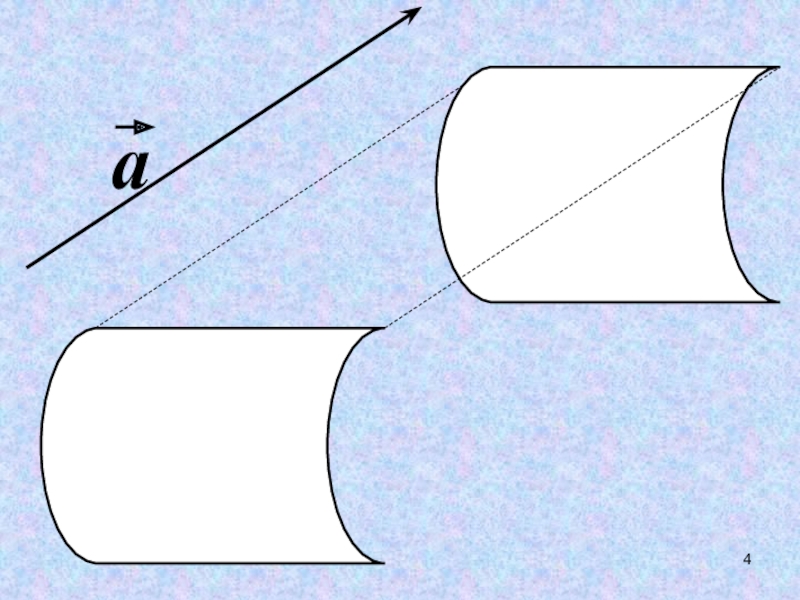
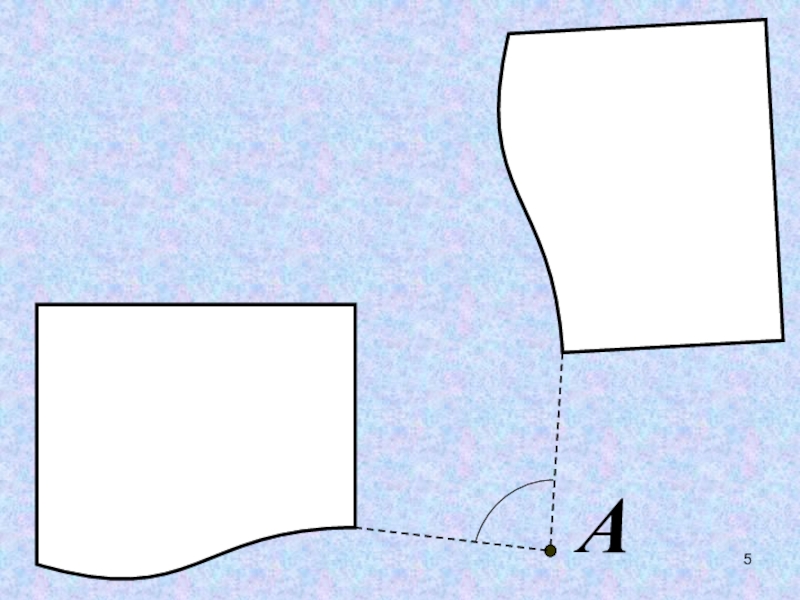
- 6. ОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПОВОРОТДВИЖЕНИЕ
- 7. Свойства движения:При движении прямая переходит в прямую,
- 8. Следствие:При движении фигура переходит в равную ей фигуру!!!
- 9. ГОМОТЕТИЯ.Гомотетия – одно из важнейших преобразований подобия.
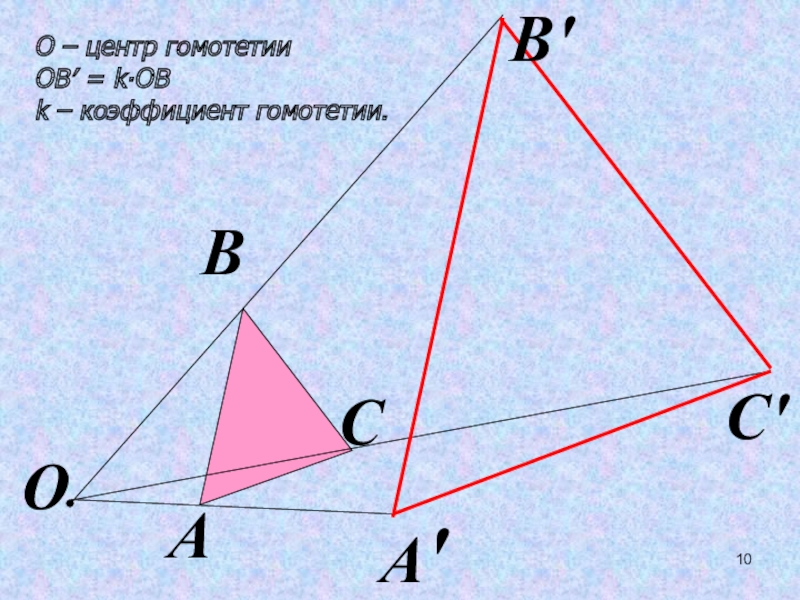
- 10. О – центр гомотетииОВ′ = k∙ОВk – коэффициент гомотетии.ОАА′ВВ′СС′
- 11. При гомотетии сохраняются только углы!!!
- 12. Рассмотрим случаи:1 случай: k > 0 а)
- 13. 1 случай а) k = 2ООА′ = 2∙ОА ОВ′ = 2∙ОВ ОС′ = 2∙ОС
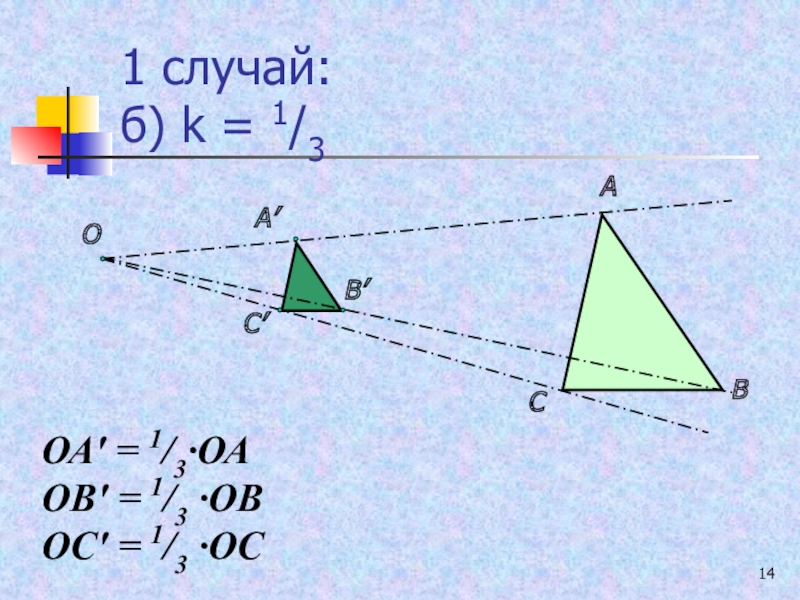
- 14. 1 случай: б) k = 1/3 АВСОА′В′С′ОА′
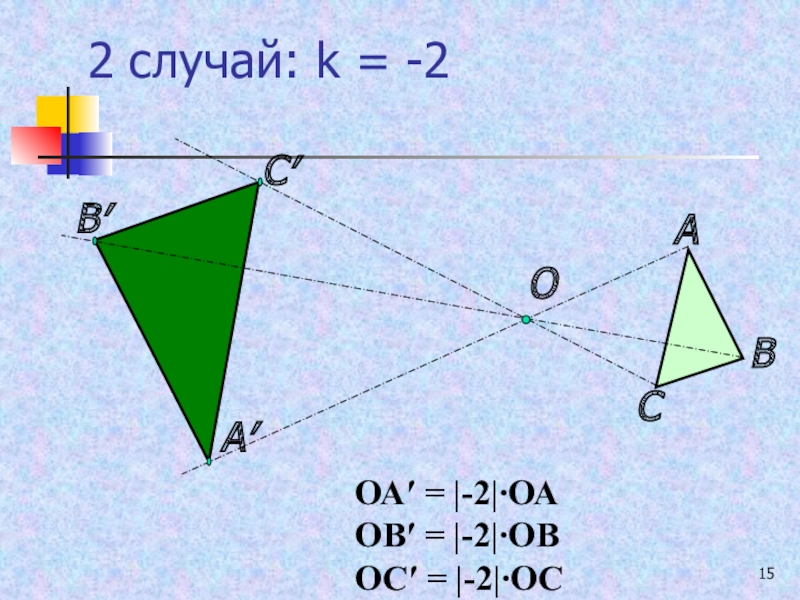
- 15. 2 случай: k = -2ОАВСА′В′С′ОА′ = |-2|∙ОА ОВ′ = |-2|∙ОВ ОС′ = |-2|∙ОС
- 16. Подобие фигурПреобразование фигуры F в фигуру F'
- 17. ГомотетияЗафиксируем точку O и положительное число k.
- 18. В геометрии фигуры одинаковой формы
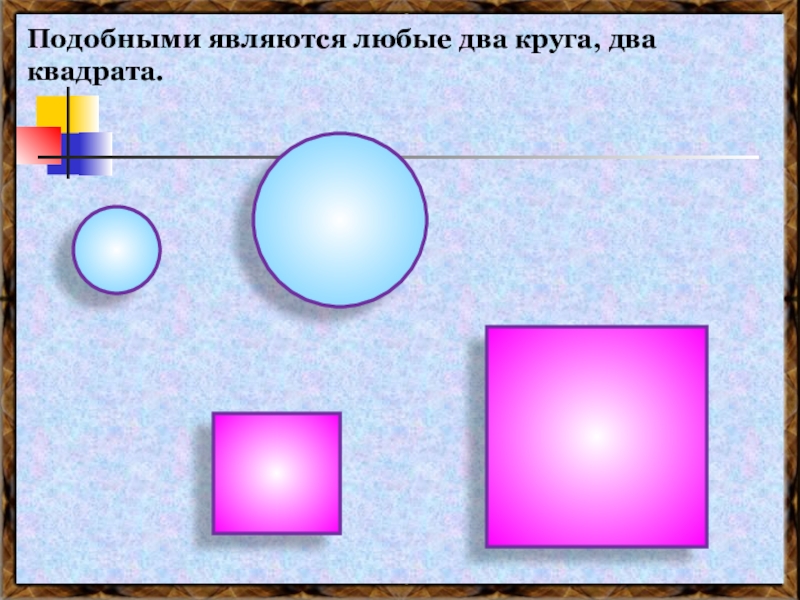
- 19. Подобными являются любые два круга, два квадрата.
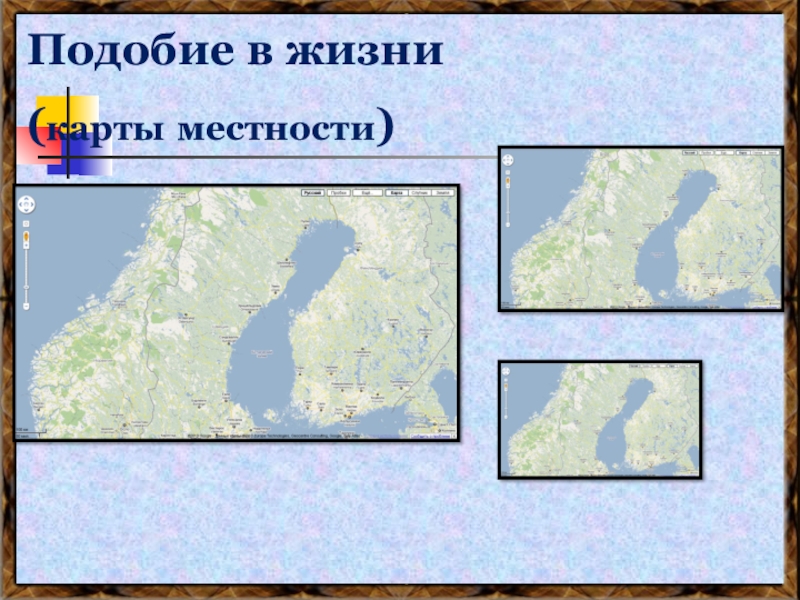
- 20. Подобие в жизни(карты местности)
- 21. Дано: ∆АВС,О – центр гомотетии,k = 3.Построить:
- 22. Подобные треугольники:АВСДва треугольника называются подобными, если их
- 23. Площади подобных фигурТеорема. Отношение площадей подобных фигур
- 24. Пример 1Периметры двух подобных многоугольников относятся как
- 25. Пример 2Как относятся стороны двух квадратов, если
- 26. Пример 3Стороны равносторонних треугольников равны 6 см
- 27. Домашнее задание: § 23, вопросы, № 23.2; 23.4(3)
- 28. СПАСИБО ЗА РАБОТУ!
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 29.04.20.
Гомотетия. Подобие фигур.
Цель урока: Рассмотреть одно из важнейших
преобразований подобия – гомотетию.
Слайд 7Свойства движения:
При движении прямая переходит в прямую, луч – в
луч, отрезок – в отрезок.
Сохраняются расстояния между точками.
Сохраняются углы между
лучами.Слайд 16Подобие фигур
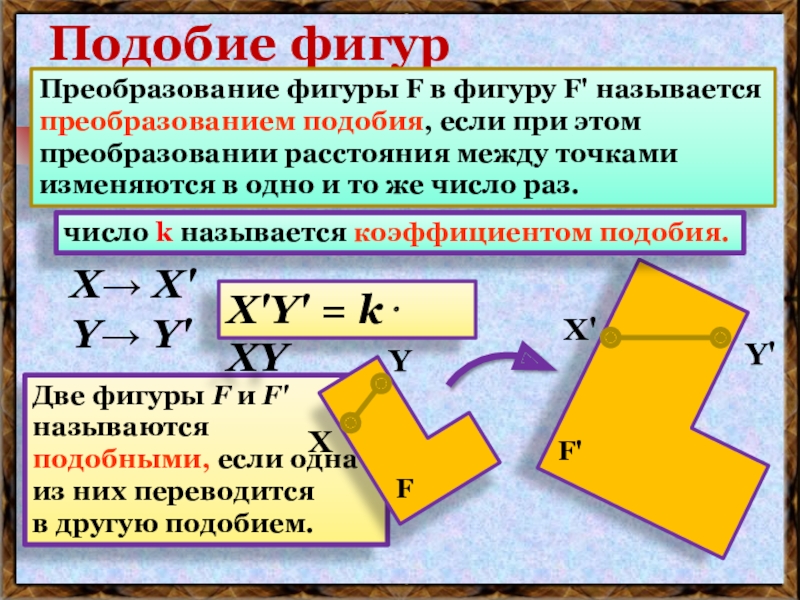
Преобразование фигуры F в фигуру F' называется преобразованием подобия,
если при этом преобразовании расстояния между точками изменяются в одно
и то же число раз.Две фигуры F и F' называются подобными, если одна из них переводится в другую подобием.
F
F'
Y
Х
Y'
Х'
Х Х'
Y Y'
Х'Y' = k ХY
число k называется коэффициентом подобия.
Слайд 17Гомотетия
Зафиксируем точку O и положительное число k. Каждой точке Х
плоскости, отличной от O сопоставим точку Х' на луче OХ
так, что OХ' = k OХ. Точке O сопоставим ее саму.O
Х
Х'
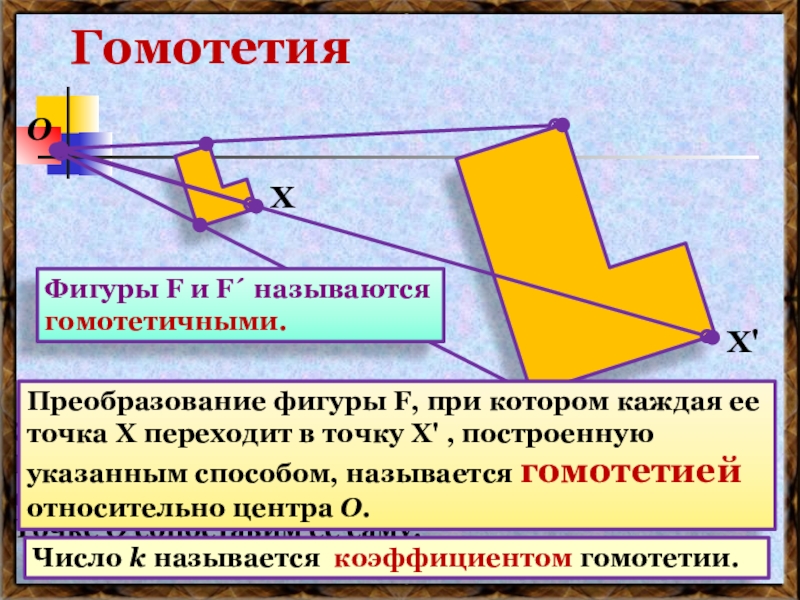
Преобразование фигуры F, при котором каждая ее точка Х переходит в точку Х' , построенную указанным способом, называется гомотетией относительно центра O.
Число k называется коэффициентом гомотетии.
Фигуры F и F´ называются гомотетичными.
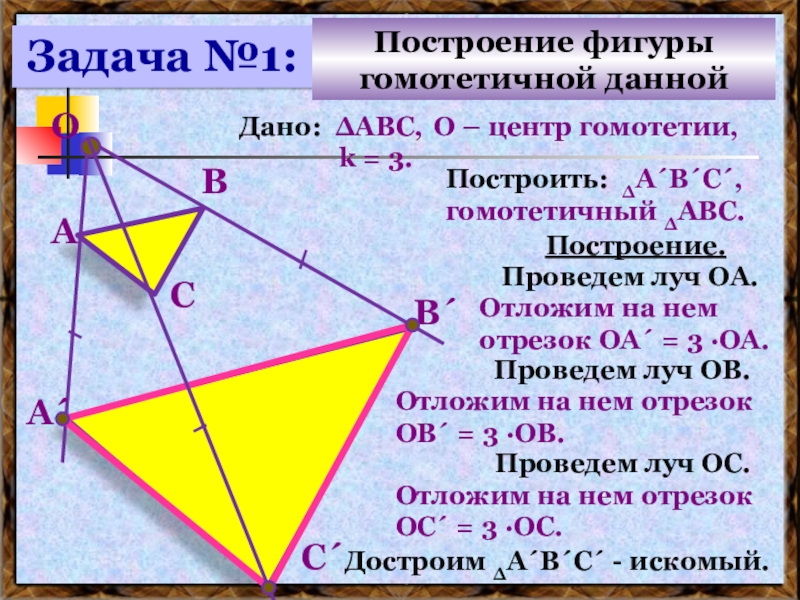
Слайд 21Дано: ∆АВС,
О – центр гомотетии,
k = 3.
Построить: ∆А´В´С´, гомотетичный ∆АВС.
Построение.
А
В
С´
А´
В´
С
Проведем луч ОА.
Отложим на нем
отрезок ОА´ = 3 ∙ОА.Проведем луч ОС.
Проведем луч ОВ.
Отложим на нем отрезок ОС´ = 3 ∙ОС.
Отложим на нем отрезок ОВ´ = 3 ∙ОВ.
Достроим ∆А´В´С´ - искомый.
О
Задача №1:
Построение фигуры
гомотетичной данной
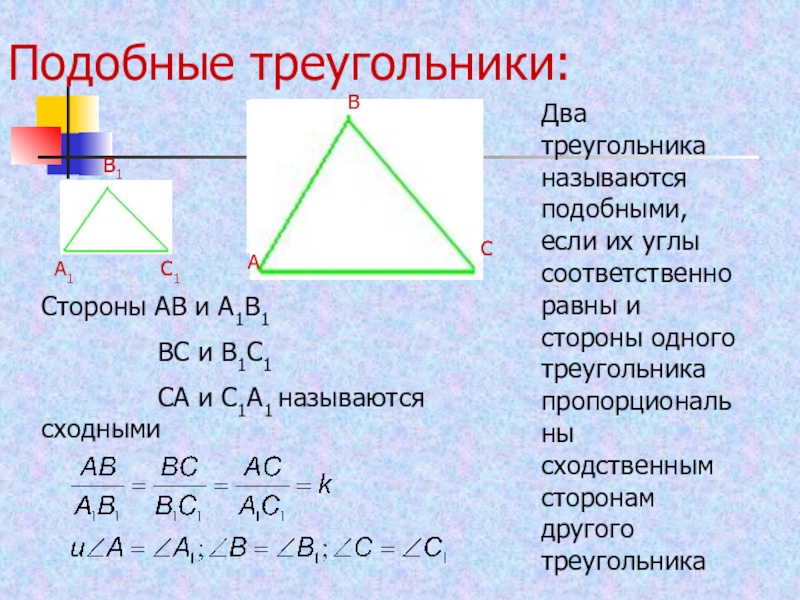
Слайд 22Подобные треугольники:
А
В
С
Два треугольника называются подобными, если их углы соответственно равны
и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
Стороны АВ
и А1В1ВС и В1С1
СА и С1А1 называются сходными
А1
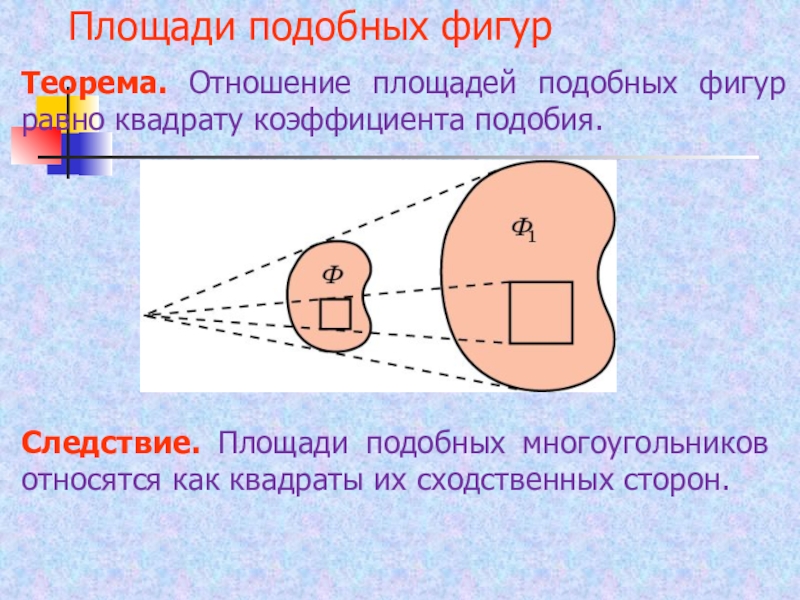
Слайд 23Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента
подобия.
Следствие. Площади подобных многоугольников относятся как квадраты их сходственных сторон.
Слайд 24Пример 1
Периметры двух подобных многоугольников относятся как 1 : 2.
Как относятся их площади?
Ответ: 1 : 4.
Слайд 25Пример 2
Как относятся стороны двух квадратов, если отношение площадей этих
квадратов равно: а) 4 : 9; б) 3 : 4;
в) 0,5 : 2?Ответ: а) 2 : 3;
в) 1 : 2.