3.2.2. Электрический ток в металлах

металлах был поставлен
ряд специальных опытов
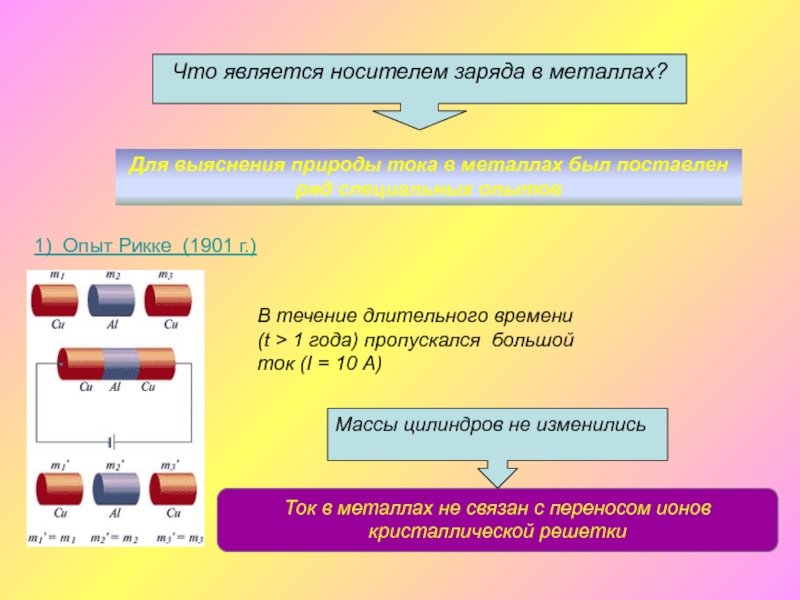
Что является носителем заряда в

металлах?

В течение длительного времени (t > 1 года) пропускался большой ток (I = 10 А)

Ток в металлах не связан с переносом ионов кристаллической решетки

Массы цилиндров не изменились

вращения составляла 300 м/с). К выводам катушки прикреплялся чувствительный гальванометр.

При резком торможении катушки через гальванометр протекал кратковременный ток. По направлению отклонения стрелки определили, что ток в металлах образуется отрицательно заряженными частицами. По величине отклонения стрелки гальванометра определили прошедший через него заряд, а затем и удельный заряд частиц , создающих ток.    

2)  Опыт Толмэна-Стюарта (1916 г.)

число заряженных частиц, прошедших через гальванометр;
n - их концентрация.
S -

площадь поперечного сечения проволоки;
l - ее длина.

проводимости под действием электрического поля.
Изменение энергии частиц идет на

выделение джоулевого тепла в проводнике:

Отсюда: -ml·dv=q0R·dq

где dv=0-v; dq=q-0=q

Что практически совпадает с удельным зарядом электрона:

классической электронной теории: дал теорию электронной проводимости металлов, теорию поляризации

света, отражённого от металлической поверхности, теорию дисперсии света.

Впервые обнаружил и объяснил аномальную дисперсию диэлектрической проницаемости). Предложил методы измерения диэлектрической проницаемости и показателя поглощения жидких диэлектриков в метровом и дециметровом диапазонах электромагнитных волн.
Член Берлинской АН

Классическая Электронная Теория
электорпроводимости металлов
(теория Друде-Лоренца)

КЭТ

валентные оболочки перекрываются. Внешние электроны, наиболее слабо связанные с атомом,

при этом отщепляются и становятся свободными. Атом становится положительным ионом. Переходя от атома к атому, электрон становится собственностью уже не отдельного атома, а всего кристалла в целом. Положительные ионы кристаллической решетки удерживаются вместе за счет взаимодействия со всеми свободными электронами. Такой вид связи атомов называется металлической связью.

Согласно КЭТ свободные электроны в металлах движутся и взаимодействуют с ионами кристаллической решетки подобно молекулам идеального газа. Они образуют электронный газ. Для электронного газа справедливы те же статистические закономерности, что и для идеального газа.

металлических проводников.
1. Закон Ома.
Средняя скорость направленного движения электронов в металле

равна его средней арифметической скорости за время свободного пробега :

Обозначим удельную проводимость вещества 

Тогда

j = E

отдает всю энергию, приобретенную им за время свободного пробега:
С учетом
Выделяющаяся

в проводнике теплота определяется потерями кинетической энергии всеми N электронами проводимости: Q = NWk = nVWk

Удельная тепловая мощность:

w = E2

проводимости  вещества прямо пропорционально температуре:
Закон Фурье для теплопроводности:

этих вопросов.
1. Температурная зависимость сопротивления.
По КЭТ должно быть

КЭТ
Однако

из опыта известно, что , т. е.

ОПЫТ!

температурах равна:
Обладая тепловой энергией, электронный газ должен вносить вклад в

теплоемкость кристалла. Теплоемкость металла складывается из теплоемкости кристаллической решетки и теплоемкости электронного газа.

Но согласно эмпирическому закону Дюлонга-Пти:

Следовательно, наличие электронного газа никак не сказывается на значении теплоемкости металлов, что необъяснимо в рамках классической теории

с экспериментальным значением, необходимо допустить, что средняя длина свободного пробега

в сотни раз превышает постоянную решетки. Для этого электроны должны проходить сотни междоузельных расстояний, не сталкиваясь с ионами. Это противоречит основным положениям классической электронной теории электропроводности металлов.

4. Коэффициент в законе Видемана-Франца.

Значение коэффициента , полученного Друде, оказалось близким к экспериментальным данным.
Лоренц попробовал уточнить его, учтя максвелловское распределение молекул по скоростям и получил ,
что еще хуже согласуется с опытом.

Сейчас мы знаем, что истинное значение

затруднения связаны с тем, что классическая теория не учитывает ряд

специфических свойств электронов. Эти свойства были установлены позднее, и на их основе была создана новая теория движения элементарных частиц – квантовая механика.

Тем не менее, в большинстве случаев классическая электронная теория электропроводности металлов дает правильные результаты, являясь в то же время более простой и наглядной, чем квантовая механика.

Закон Ома для электролитов.
Электролиз. Законы электролиза.
Применение электролиза.

разряд. Ток насыщения.
Самостоятельный газовый разряд.
Виды самостоятельного разряда (условия, механизм возникновения,

применение):
4.1. Тлеющий разряд.
4.2. Искровой разряд.
4.3. Коронный разряд.
4.4. Дуговой разряд.
5. Плазма.