Слайд 14. Динамические модели с бесконечным плановым периодом
Слайд 2В большинстве рассмотренных выше моделей:
будущее, находящееся за пределами заранее
установленного планового периода, практически не принимается во внимание.
В некоторых случаях
удается доказать теорему о длительности планового периода;
в других случаях – выбор тех или иных «конечных» условий.
Слайд 3Далее рассматриваются модели, в которых длительность планового периода предполагается бесконечной.
Для
получения решения в таких моделях необходимо дополнительное ограничение: допущение о
стационарности.
В простейшем случае предполагается:
все функции экономического эффекта, выбираемой программы и внешние условия (например, объем спроса) для каждого из плановых отрезков одинаковы.
Слайд 4В реальной действительности стационарность редко сохраняется в течение длительных периодов
возникает вопрос о практической значимости моделей, основанных на предположении о
стационарности в течение бесконечного планового периода.
Обоснование значимости – на примерах ситуаций двух типов.
Слайд 51. Использование динамических оптимизационных моделей для улучшения текущих оперативных решений
(например, о пополнении запасов и разработке графиков производства).
Пример.
Ежедневный контроль запасов
и пополнение запасов (закупка) при достижении некоторого критического значения уровня запасов.
Если спрос, а также затраты на покупку и хранение устойчивы в течение 12 месяцев, то один из возможных подходов – построение оптимальной программы для планового периода длительностью 365 дней и использование этой программы в течение нескольких первых месяцев.
Модель с бесконечным плановым периодом может дать хорошие результаты и требует намного меньших объемов вычислений
Слайд 62. Использование динамических оптимизационных моделей при принятии повторяющихся решений о
распределении капитальных вложений (например, о замене дорогостоящего оборудования).
При принятии решения
о приобретении нового оборудования учет затрат на его будущие повторные замены может привести к лучшим решениям, чем отказ от учета будущего.
Слайд 7Проблема выбора оптимального решения при бесконечном плановом периоде
Конечный плановый период:
в
начале любого отрезка необходимо знать состояние системы и число оставшихся
отрезков;
об оптимальности программы можно судить по сумме конечной последовательности значений локального дохода.
Бесконечный плановый период:
любая программа (стратегия) обусловливает бесконечную последовательность значений локального дохода
необходим способ сравнения стратегий.
Слайд 8Если одна стратегия обеспечивает бóльший эффект, чем другая, для любой
фиксированной длительности планового периода, то результат сравнения очевиден.
Проблема:
как
выбрать решение, если одна и та же стратегия представляется лучшей для одной длительности планового периода и худшей для другой.
Слайд 9Пример.
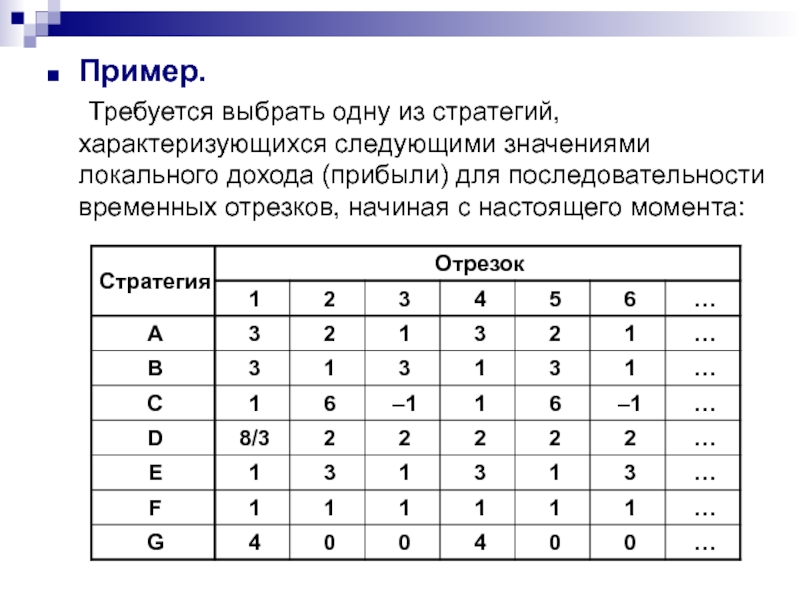
Требуется выбрать одну из стратегий, характеризующихся следующими значениями локального дохода
(прибыли) для последовательности временных отрезков, начиная с настоящего момента:
Слайд 10Разумно сразу исключить вариант F, т. к. стратегия А для
каждого из отрезков обеспечивает лучшие (или по меньшей мере не
худшие) результаты – А доминирует над F.
Можно также обосновать исключение варианта Е, т. к. стратегия D для любого отрезка обеспечивает бóльшую совокупную прибыль (прибыль с начала планового периода).
Вопрос: по какому принципу выбрать лучший из вариантов А, В, С, D и G?
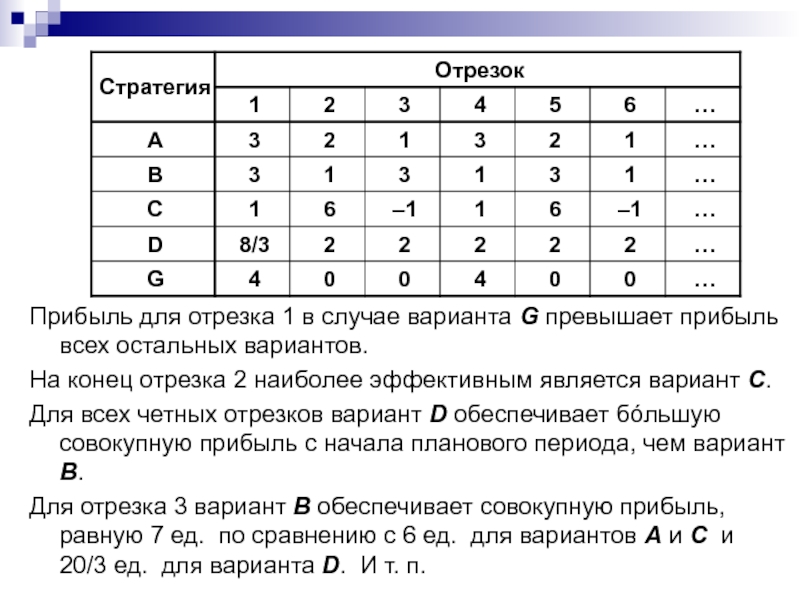
Слайд 11Прибыль для отрезка 1 в случае варианта G превышает прибыль
всех остальных вариантов.
На конец отрезка 2 наиболее эффективным является вариант
С.
Для всех четных отрезков вариант D обеспечивает бóльшую совокупную прибыль с начала планового периода, чем вариант В.
Для отрезка 3 вариант В обеспечивает совокупную прибыль, равную 7 ед. по сравнению с 6 ед. для вариантов А и С и 20/3 ед. для варианта D. И т. п.
Слайд 12Утверждать, что один из вариантов А, В, С, D или
G является лучшим, можно только на основе дополнительных допущений.
На основе
того или иного допущения –
формулы, позволяющие преобразовать бесконечную последовательность значений локального дохода в одно число (критерий), характеризующее «относительное качество» соответствующей программы (стратегии).
Слайд 13Критерии качества стратегий
Средняя величина дохода за отрезок.
На практике
этот критерий используется чаще всего в случаях, когда экономический эффект
измеряется уровнем затрат.
Тогда рекомендуется правило выбора: следует выбрать стратегию, которой отвечают наименьшие средние затраты за отрезок.
Интегральный доход, дисконтированный к настоящему моменту времени (интегральный дисконтированный доход).
При использовании этих двух критериев не всегда выбираются одинаковые стратегии!
Слайд 14 Эквивалентный средний доход.
При использовании этого критерия часто удается определить
вид оптимальной стратегии; затем можно вычислить конкретные численные значения: среднего
дохода за отрезок, или интегрального дисконтированного дохода.
Этот критерий в некотором смысле аналогичен широко применяемому в отечественной практике критерию приведенных затрат.
Слайд 15Критерий среднего дохода за отрезок
Допущение: для ЛПР имеет одинаковое значение
получение единицы дохода на любом из отрезков.
Это означает: получение дохода
на более раннем отрезке не дает каких-либо преимуществ по сравнению с его получением позже.
Целесообразно рассмотреть средний доход за отрезок при бесконечно возрастающем числе отрезков, выбирая вариант с наибольшим средним доходом.
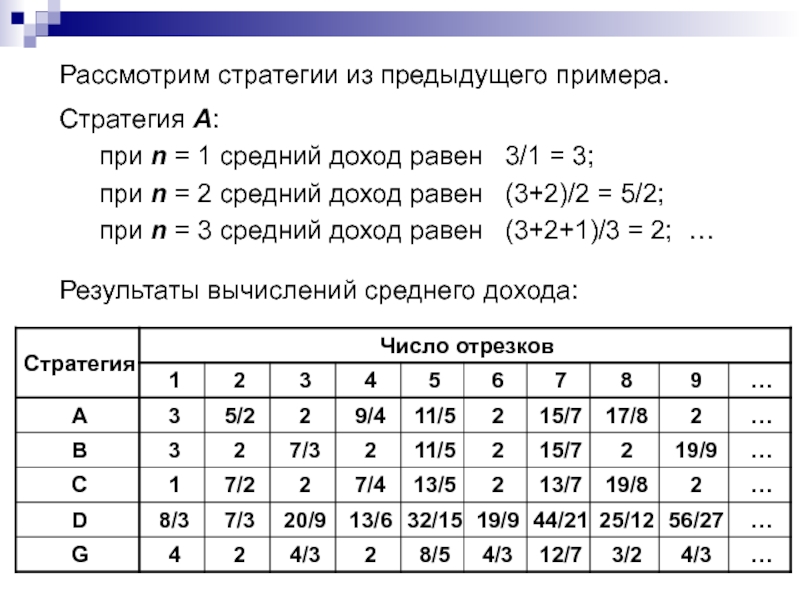
Слайд 16Рассмотрим стратегии из предыдущего примера.
Стратегия А:
при n = 1
средний доход равен 3/1 = 3;
при n = 2
средний доход равен (3+2)/2 = 5/2;
при n = 3 средний доход равен (3+2+1)/3 = 2; …
Результаты вычислений среднего дохода:
Слайд 17Можно вывести формулы для общих членов последовательностей средних доходов за
отрезок.
Стратегия А:
при n = 3k + 1,
k = 0, 1, 2, …
при n = 3k + 2, k = 0, 1, 2, …
при n = 3k, k = 1, 2, …
Слайд 18 Стратегия В:
при n = 2k + 1,
k = 0, 1, 2, …
при n =
2k, k = 1, 2, …
Слайд 19 Стратегия С:
при n = 3k + 1,
k = 0, 1, 2, …
при n =
3k + 2, k = 0, 1, 2, …
при n = 3k, k = 1, 2, …
Слайд 20 Стратегия D:
при любых n = 1, 2,
…
Слайд 21 Стратегия G:
при n = 3k + 1,
k = 0, 1, 2, …
при n =
3k + 2, k = 0, 1, 2, …
при n = 3k, k = 1, 2, …
Слайд 22Итог:
для стратегий А, В, С и D величина среднего дохода
за отрезок стремится к 2 при n → ∞ ;
для
стратегии G эта величина стремится к 4/3.
Вывод:
в предположении об отсутствии временнóй предпочтительности дохода стратегии А, В, С и D являются одинаково предпочтительными (несмотря на то, что для любого конечного планового периода их эффективность различна);
стратегия G – менее предпочтительной.
Слайд 23Очевидный недостаток критерия среднего дохода за отрезок: полная нечувствительность этого
критерия к величине дохода за
конечное число отрезков.
Иллюстрация.
Пусть имеется вариант А', показатели которого полностью идентичны показателям варианта А, за исключением того, что прибыль на отрезке 1 для А' равна не 3, а 100 ед.
С точки зрения критерия среднего дохода за отрезок варианты А и А' являются одинаково предпочтительными.
Слайд 24Другой недостаток:
этот критерий неприменим, если при бесконечном возрастании числа отрезков
бесконечно возрастает и средний доход за отрезок.
Необходимое условие применения данного
критерия:
для сравниваемых последовательностей должен существовать конечный предел среднего дохода за отрезок.
Слайд 25Критерий интегрального дисконтированного дохода
Подход к соизмерению бесконечных последовательностей:
вычисление так
называемых интегральных показателей дохода, дисконтированных к настоящему моменту времени.
Слайд 26Пусть последовательность значений дохода имеет вид
R1, R2, R3, … ,
Rn, …
Интегральный дисконтированный доход равен
где
коэффициент дисконтирования за отрезок,
i – процентная ставка за отрезок.
Допущение:
для данного предприятия может быть определено адекватное значение i.
Слайд 27Обоснование допущения – учет внешних условий.
Пример.
Пусть предприятие может как брать
взаймы, так и ссужать любую сумму денег при оплате по
правилу сложных процентов при фиксированной процентной ставке, равной i% за отрезок.
Тогда, взяв взаймы 1 д. е.,
через год необходимо вернуть (1 + i /100) д. е.,
через два года – (1 + i /100)2 д. е., ………
через n лет – (1 + i /100)n д. е.
Аналогично:
1 д. е., которая будет получена через n лет, в настоящий момент эквивалентна (1 + i /100)–n д. е.
Слайд 28При данном подходе предполагается: полезность денежных поступлений и затрат в
разные моменты времени неодинакова
для перераспределения дохода во времени ЛПР,
возможно, на одних отрезках пожелает брать ссуды, а на других – давать взаймы.
Какова бы ни была система предпочтений денег во времени, наилучший выбор – это выбор варианта, которому соответствует наибольший интегральный дисконтированный доход.
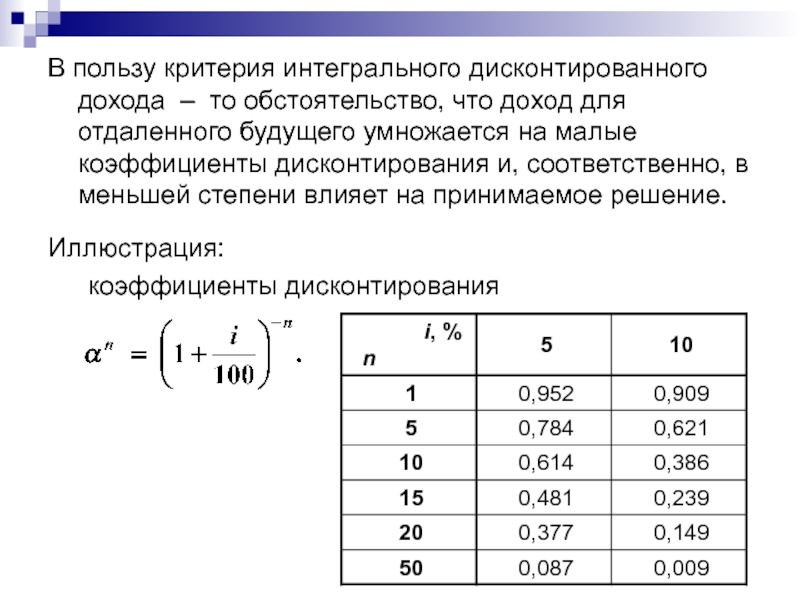
Слайд 29В пользу критерия интегрального дисконтированного дохода – то обстоятельство, что
доход для отдаленного будущего умножается на малые коэффициенты дисконтирования и,
соответственно, в меньшей степени влияет на принимаемое решение.
Иллюстрация:
коэффициенты дисконтирования
Слайд 30Вопрос: всегда ли является конечной сумма
бесконечного числа слагаемых в формуле (4.1)?
Пусть значения дохода R
для всех отрезков одинаковы.
Тогда интегральный дисконтированный доход (ИДД) равен
геометрическая прогрессия;
при 0 ≤ α < 1
Слайд 31Пример.
Вычислим ИДД для стратегий из предыдущего примера, предполагая, что 0
≤ α < 1.
Для стратегии А:
Для стратегии В:
Слайд 32 Для стратегии С:
Для стратегии D:
Для стратегии G:
Слайд 33Сопоставление стратегий:
ИДД(А) – ИДД(В) =
ИДД(А) > ИДД(В);
стратегию В можно
исключить как доминируемую.
Слайд 34 ИДД(А) – ИДД(С) =
ИДД(А) > ИДД(С);
стратегию С можно исключить
как доминируемую.
Слайд 35 ИДД(А) – ИДД(D) =
ИДД(А) > ИДД(D);
стратегию D можно исключить
как доминируемую.
Слайд 36 ИДД(А) – ИДД(G) =
при
стратегия А более
предпочтительна, чем G;
при стратегия G более предпочтительна, чем A;
при стратегии А и G одинаково предпочтительны.
Слайд 37Если процентная ставка очень высока (значение α мало), то получение
при варианте G 4 ед. прибыли на первом отрезке оказывает
бóльшее влияние, чем получение более поздних выгод при варианте А.
В общем случае:
чем меньше α, тем больше значение ранних эффектов;
в пределе при α = 0 оказывает влияние только прибыль первого отрезка R1.
Слайд 38При дисконтировании могут разрешиться проблемы, возникающие в ряде случаев при
применении критерия среднего дохода, связанные с бесконечным возрастанием среднего дохода
за отрезок.
Но: и сумма ряда (4.1) не всегда конечна.
Слайд 39Критерий эквивалентного среднего дохода
Это подход, связывающий понятия средних и дисконтированных
значений.
Основан на идее построения бесконечной последовательности значений дохода, для которой
значение
ИДД является таким же, как для исходной последовательности;
значения дохода (до дисконтирования) на всех отрезках одинаковы.
Это общее значение интерпретируется как эквивалентный средний доход данной последовательности.
Слайд 40Пусть ИДД для стратегии X при некотором фиксированном значении α
составляет Р(α).
Рассмотрим новую последовательность, в которой недисконтированный доход для
любого отрезка n равен
Rn = (1 – α)∙P(α). (4.2)
Для этой последовательности
Последовательность (4.2) характеризуется тем же значением ИДД, что и стратегия X, а величина (1 – α)∙P(α) есть эквивалентный средний доход.
Слайд 41При любом фиксированном значении α, 0 ≤ α < 1,
использование критерия эквивалентного среднего дохода приводит к выбору тех же
вариантов, что и использование критерия интегрального дисконтированного дохода.
Причина:
значение эквивалентного среднего дохода (ЭСД) получается путем умножения ИДД на коэффициент (1 – α), одинаковый для всех стратегий.
Слайд 42Пример.
Вычислим ЭСД для стратегий из предыдущего примера.
Слайд 43Важно:
во всех случаях, когда средний доход за отрезок определен (предел
конечен), его можно получить из формулы ЭСД предельным переходом при
α → 1-0.
Для рассматриваемого примера при α = 1:
ЭСД не всегда определен при α = 1
Слайд 44С точки зрения критерия эквивалентного среднего дохода при α =
1 варианты А, В, С и D в равной степени
предпочтительны.
Действительно ли это так?
Окончательный ответ – за ЛПР.
Можно привести веские доводы в пользу того, что при α = 1
оптимальной следует считать стратегию А;
стратегии С и D – близкими к оптимальным;
стратегию В исключить из рассмотрения.
Слайд 45Из
ИДД(А) – ИДД(В) =
ИДД(А) – ИДД(С) =
ИДД(А) – ИДД(D) =
Слайд 46При значении α, близком к 1, дисконтированный доход для варианта
А больше, чем для вариантов В, С и D;
при
α = 1 ИДД(А) – ИДД(С) = 0, и ИДД(А) – ИДД(D) = 0, варианты С или D почти столь же хороши, как и вариант А;
при α = 1 ИДД(А) – ИДД(В) = 1/6 вариант В менее предпочтителен и должен быть исключен (несмотря на то, что ЭСД(А) = ЭСД(В) ).
Слайд 47Выводы о выборе критерия оптимальности в динамических моделях:
метод соизмерения последовательностей
значений дохода должен включать то или иное допущение о предпочтительности
денежных поступлений и затрат во времени;
метод сведения бесконечных последовательностей к некоторому конечному числу не обязательно применим к любой такой последовательности;
даже если с помощью некоторого метода две различные последовательности сводятся к одному и тому же числу, соответствующие стратегии не обязательно являются одинаково предпочтительными, если учитывать другие соображения экономического характера.
Слайд 48Модель восстановления с бесконечным числом этапов
Типичный пример модели восстановления –
задача замены оборудования.
Период восстановления начинается каждый раз, когда заменяется оборудование
(восстановление в том смысле, что необходимо заново принимать решение о сроке следующей замены).
Управляемые переменные – последовательные интервалы времени между моментами замены.
Далее – построение и анализ общей модели.
Слайд 49Пусть
момент восстановления можно выбирать из N альтернативных вариантов, которым
присвоены индексы k = 1, 2, . . ., N;
если вариант k выбран в момент восстановления t, то следующий момент восстановления наступит на отрезке (t + k).
Обозначим
Rk – затраты варианта k при их оценке в начале его периода восстановления.
Здесь – допущение о стационарности: Rk не зависит от того, о каком именно периоде восстановления идет речь.
Цель оптимизации – достижение минимума затрат
Слайд 50Конечный плановый период.
Обозначим:
fn – интегральные дисконтированные затраты для
оптимальной стратегии восстановления, при которой один из альтернативных
вариантов должен быть выбран за n отрезков до конца планового периода.
Пусть выбран вариант k, тогда затраты составят Rk .
Если в следующий момент восстановления (на отрезке (n – k)) также принимается оптимальное решение, то дальнейшие затраты составят αk∙fn–k ,
где αk – коэффициент дисконтирования будущих затрат к настоящему моменту.
Слайд 51За n отрезков до конца планового периода
при n ≥
N оптимальной является стратегия, определяемая рекуррентным соотношением
при n < N
минимум отыскивается при k = 1, 2, ... , n.
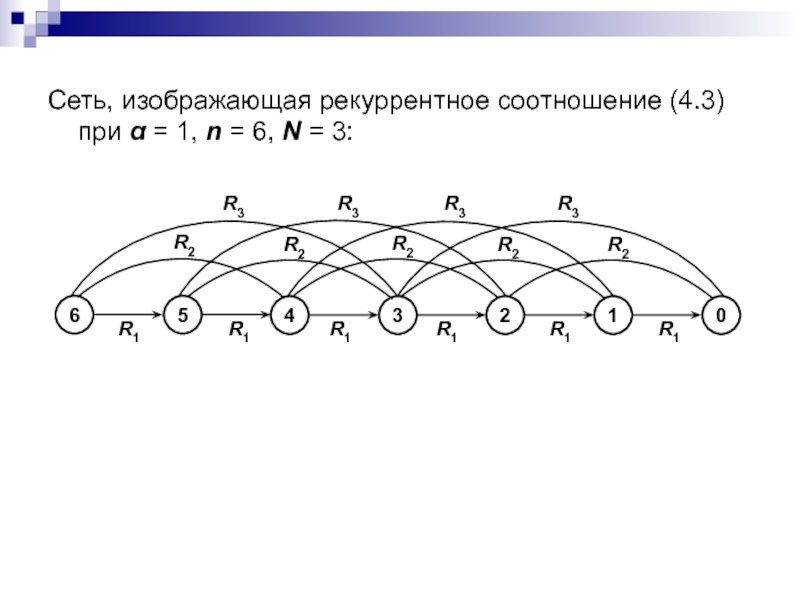
Слайд 52Сеть, изображающая рекуррентное соотношение (4.3) при α = 1, n
= 6, N = 3:
Слайд 53Иллюстрация.
В частности, если для всех плановых периодов длительностью n отрезков
значение k = 1 является оптимальным, то из (4.3)
Слайд 54Бесконечный плановый период.
Каждый раз, когда наступает очередной момент восстановления, принятие
решения осуществляется в условиях бесконечного планового периода.
Можно доказать:
существует оптимальная
стратегия, которая является стационарной, т. е. в каждый момент восстановления выбирается один и тот же вариант k.
Тогда при α ≠ 1 соответствующим обобщением (4.3) является рекуррентное соотношение
Функциональное (экстремальное) уравнение
Слайд 55В отношении экстремальных уравнений ставятся вопросы:
имеется ли у данного уравнения
конечное решение;
если имеется, то является ли это решение единственным;
если решение
единственно, то является ли f максимальным значением дисконтированного дохода для всех (не обязательно стационарных) стратегий.
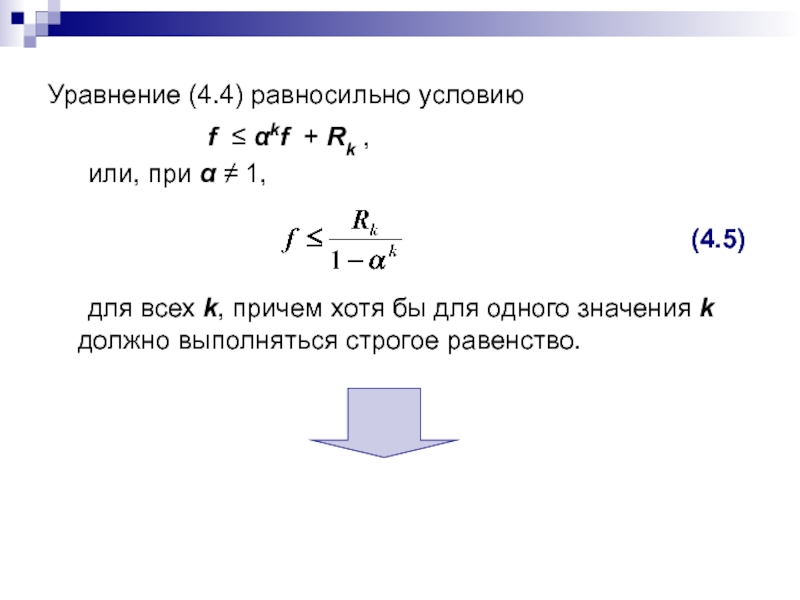
Слайд 56Уравнение (4.4) равносильно условию
f ≤ αkf + Rk ,
или, при
α ≠ 1,
для всех k, причем хотя бы для
одного значения k должно выполняться строгое равенство.
Слайд 57Уравнение (4.4) при α ≠ 1 имеет однозначное конечное решение,
равное
Оптимальная стационарная стратегия соответствует выбору любого k, которое позволяет получить
оптимальное значение f.
Замечание.
Минимизируемое выражение совпадает с ИДД для стационарной стратегии:
Слайд 58При α = 1 уравнение (4.4) неприменимо по следующей причине:
если
допустить, что при любом k Rk > 0, то ни
одно конечное значение f не удовлетворяет (4.4)
(для некоторого k получим f = f + Rk – невозможно при Rk > 0);
если допустить, что при любом k Rk = 0, тогда любое конечное значение f удовлетворяет (4.4).
Слайд 59Если в уравнении (4.4) заменить f на эквивалентный средний доход
g
= (1 – α)∙f ,
то после преобразований (4.6) примет вид
Соотношение
(4.7) можно использовать при 0 ≤ α ≤ 1:
при 0 ≤ α < 1 стратегия, оптимальная согласно (4.6), будет оптимальной и согласно (4.7);
при α = 1 оптимальная стратегия определяется в соответствии с
Минимизация средних затрат за отрезок
Слайд 60Одно из возможных направлений использования соотношения (4.8) – стационарная модель
управления производством и запасами с вогнутой функцией затрат.
Слайд 61Выпуклые и вогнутые функции
Функция g(x), определенная при целочисленных значениях х,
называется выпуклой, если
g(x + 1) – g(x) ≥ g(x) –
g(x – 1)
или
и вогнутой, если
g(x + 1) – g(x) ≤ g(x) – g(x – 1)
или
Слайд 62Если g(x) – общая сумма затрат, то
функция затрат будет
выпуклой, если каждая дополнительная единица продукции стóит не меньше предыдущей;
функция
затрат будет вогнутой, если каждая дополнительная единица продукции стóит не больше предыдущей.
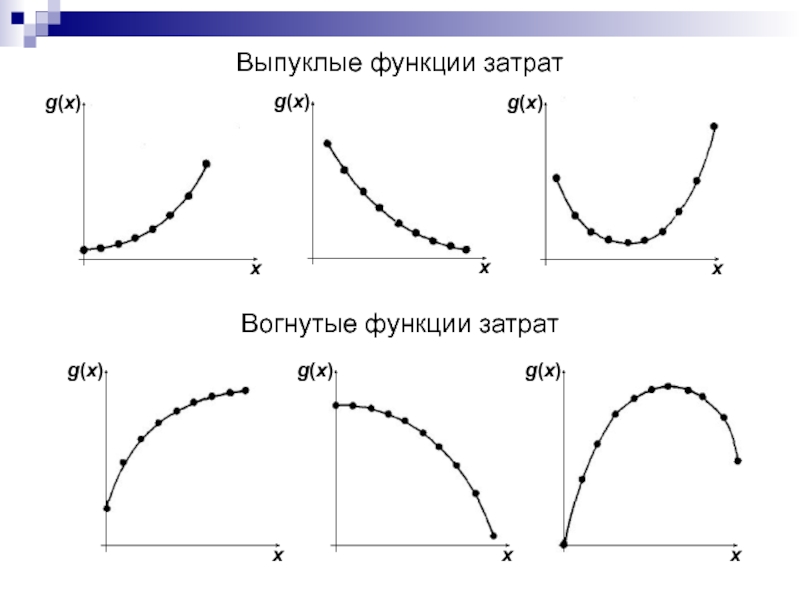
Слайд 63Выпуклые функции затрат
Вогнутые функции затрат
Слайд 64Примеры.
Пусть g(x) = a∙x + b.
Тогда
Вывод: линейная функция для любых
х одновременно является и выпуклой, и
вогнутой.
Слайд 65Пусть g(x) = a∙x2 + b.
Тогда
Вывод: данная функция для любых
х
выпукла при неотрицательном а,
вогнута при неположительном а.
Слайд 66Пусть
где b ≥ 0.
Результаты примера 1):
при х > 1
функция одновременно является и выпуклой, и вогнутой.
При х =
1:
Вывод: данная функция для неотрицательных х является вогнутой.
Слайд 67Пусть
Показать самостоятельно:
функция является
выпуклой при а1 ≤ а2 ≤ а3
,
вогнутой при а1 ≥ а2 ≥ а3 .
Указание: выполнить анализ
при х = w1 и х = w2 .
Слайд 68Пусть функции затрат на производство продукции и содержание запасов являются
стационарными и имеют вид
ht(it) = h∙it
для всех t,
где s ≥ 0, с ≥ 0 и h > 0;
хt – объем выпуска продукции на отрезке t (или размер заказа в начале отрезка t);
it – уровень запасов на конец отрезка t.
Стационарная модель управления производством и запасами с вогнутой функцией затрат
Слайд 69Предположим
спрос является стационарным: Dt = D для всех t,
спрос
должен быть полностью и своевременно удовлетворен.
Обозначим:
Q – объем выпуска
(заказа) в момент восстановления, если исходный запас на начало планового периода равен нулю.
При конечном плановом периоде
Q = kD,
где k – положительное целое число.
Для вогнутых функций затрат
Слайд 70Предположим:
такой же характер решения сохраняется и для бесконечного планового
периода.
Тогда задача состоит в нахождении значения k, позволяющего минимизировать
средние затраты за отрезок.
Слайд 71 Rk – сумма затрат на переналадку (размещение заказа), производство
(закупку) продукции и содержание запасов:
Тогда средние затраты за отрезок
составят
Слайд 72Минимизация:
Вывод:
критическая точка является точкой минимума функции Rk/k.
Слайд 73Итог:
Выражение (4.10), определяющее оптимальное значение Q, называется формулой экономически выгодного
размера партии.
Оптимальная стратегия:
производить (заказывать)
ед. продукции
через каждые ед. времени.
Слайд 74Замечание.
Формулы (4.9) и (4.10) являются приближенными, т. к. получаемые величины
в общем случае не обязательно целочисленны.
Если найденное из (4.9) значение
k не есть целое число, то оптимальную стратегию можно найти так:
вычислить средние затраты за отрезок Rk /k для двух ближайших к k целых чисел (большего и меньшего),
выбрать лучшее из полученных значений.
Слайд 75В рассуждениях выше предполагалось, что пополнение запаса происходит мгновенно в
момент восстановления.
В реальных ситуациях существует положительный срок выполнения заказа l
(временнóе запаздывание) от момента размещения заказа до реальной поставки.
Слайд 76При l < k (время выполнения заказа меньше
продолжительности периода восстановления)
результаты (4.9) и
(4.10) остаются в силе, но:
момент возобновления наступает не тогда, когда уровень запасов становится нулевым, а когда он опускается до значения lD ед.
Слайд 77При l > k (время выполнения заказа больше
продолжительности периода восстановления)
необходимо определить эффективный
срок выполнения заказа
Обоснование:
После [l /k] циклов (длиной k каждый) ситуация становится такой, как если бы интервал между размещением одного заказа и получением другого был равен le.
Момент восстановления наступает, когда уровень запасов опускается до le∙D.
[z] означает целую часть z (наибольшее целое, не превосходящее z).
Слайд 78Пример.
Неоновые лампы в университетском городке заменяются с интенсивностью 100 штук
в день.
Стоимость размещения заказа на покупку ламп составляет $100.
Стоимость
хранения лампы на складе оценивается в $0,02 в день.
Срок выполнения заказа от момента его размещения до реальной поставки равен 12 дней.
Определим оптимальную стратегию заказа неоновых ламп.
Слайд 79По условию D = 100 шт./день,
s = $100,
h = $0,02,
l
= 12 дней.
Поэтому
период восстановления составит
дней;
оптимальный размер заказа составляет
штук;
Слайд 80 эффективный срок выполнения заказа
дня;
момент восстановления имеет
место при уровне запаса
le∙D = 2 ∙100 = 200
шт.
Оптимальная стратегия:
заказывать 1000 ламп, как только уровень их запаса уменьшается до 200 шт.
Слайд 81Структура описанной выше модели восстановления очень проста.
Задачи более общего вида
нельзя решить столь же легко: для решения требуются более сложные
методы.
В рамках динамического программирования эти методы обычно называются методами последовательного приближения.