Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Quantum mechanics
Содержание
- 1. Quantum mechanics
- 2. The Wave FunctionWe concluded on the basis
- 3. The Wave FunctionThe number of photons per
- 4. The Wave FunctionThe amplitude of the de
- 5. The Wave FunctionThis probabilistic interpretation of the
- 6. The Wave FunctionOne-Dimensional Wave Functions and Expectation
- 7. The Wave FunctionAlthough it is not possible
- 8. The Wave FunctionBecause the particle must be
- 9. The Wave FunctionFurthermore, one can find the
- 10. SOLUTIONThe Wave FunctionApply the normalization condition, to the wave function:
- 11. The Wave Function
- 12. (B) What is the expectation value of x for this particle?The Wave FunctionSOLUTIONEvaluate the expectation value:
- 13. The Wave Function
- 14. Classical physics places no restrictions on the
- 15. Analysis Model: Quantum ParticleUnder Boundary ConditionsThe wave
- 16. Analysis Model: Quantum ParticleUnder Boundary ConditionsIncorporating this
- 17. Analysis Model: Quantum ParticleUnder Boundary ConditionsA Particle in a Box
- 18. Because the wavelengths of the particle are
- 19. Analysis Model: Quantum ParticleUnder Boundary ConditionsBecause the
- 20. Analysis Model: Quantum ParticleUnder Boundary ConditionsBoundary Conditions
- 21. Analysis Model: Quantum ParticleUnder Boundary ConditionsBoundary Conditions
- 22. The Schrödinger EquationPreviously we discussed a wave
- 23. The Schrödinger EquationThe Schrödinger equation as it
- 24. The Schrödinger EquationThe Particle in a Box
- 25. The Schrödinger Equationwhere A and B are
- 26. The Schrödinger EquationEach value of the integer
- 27. A Particle in a Well of Finite
- 28. A Particle in a Well of Finite Height
- 29. A Particle in a Well of Finite Height
- 30. A Particle in a Well of Finite
- 31. Tunneling Through a Potential Energy BarrierA potential
- 32. Tunneling Through a Potential Energy BarrierThe probability
- 33. The Simple Harmonic OscillatorThe potential energy of
- 34. The Simple Harmonic OscillatorLet’s investigate how the
- 35. The Simple Harmonic OscillatorIt turns out that
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2The Wave Function
We concluded on the basis of experimental evidence
that both matter and electromagnetic radiation are sometimes best modeled
as particles and sometimes as waves, depending on the phenomenon being observed. We can improve our understanding of quantum physics by making another connection between particles and waves using the notion of probabilityWe begin by discussing electromagnetic radiation using the particle model. The probability per unit volume of finding a photon in a given region of space at an instant of time is proportional to the number of photons per unit volume at that time:
Слайд 3The Wave Function
The number of photons per unit volume is
proportional to the intensity of the radiation:
Now, let’s form a
connection between the particle model and the wave model by recalling that the intensity of electromagnetic radiation is proportional to the square of the electric field amplitude E for the electromagnetic wave:Equating the beginning and the end of this series of proportionalities gives
Слайд 4The Wave Function
The amplitude of the de Broglie wave associated
with a particle is not a measurable quantity because the
wave function representing a particle is generally a complex function as we discuss below. In contrast, the electric field for an electromagnetic wave is a real function. The matter analog to Equation 41.1 relates the square of the amplitude of the wave to the probability per unit volume of finding the particle. Hence, the amplitude of the wave associated with the particle is called the probability amplitude, or the wave function, and it has the symbol Ψ.Слайд 5The Wave Function
This probabilistic interpretation of the wave function was
first suggested by Max Born (1882–1970) in 1928. In 1926,
Erwin Schrцdinger proposed a wave equation that describes the manner in which the wave function changes in space and time.The Schrцdinger represents a key element in the theory of quantum mechanics.
Слайд 6The Wave Function
One-Dimensional Wave Functions and Expectation Values
The probability that
the particle will be found in the infinitesimal interval dx
around the point x isСлайд 7The Wave Function
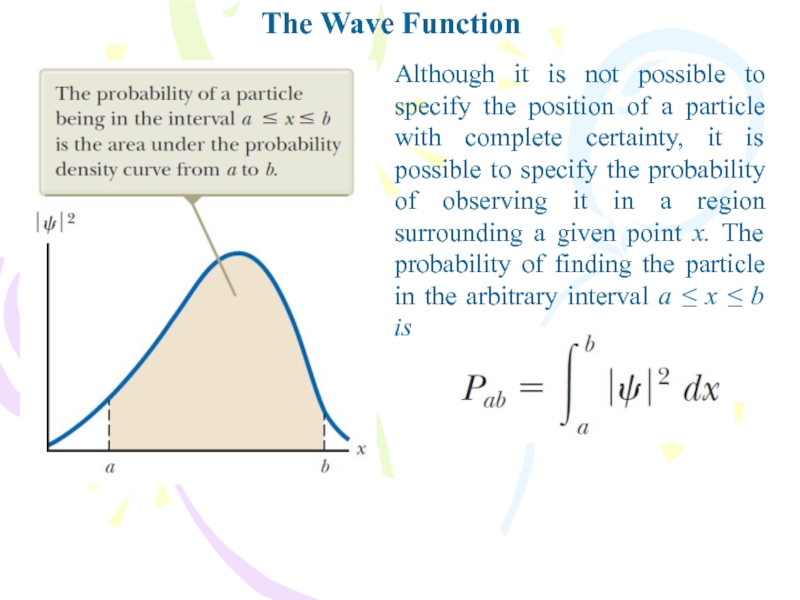
Although it is not possible to specify the
position of a particle with complete certainty, it is possible
to specify the probability of observing it in a region surrounding a given point x. The probability of finding the particle in the arbitrary interval a ≤ x ≤ b isСлайд 8The Wave Function
Because the particle must be somewhere along the
x axis, the sum of the probabilities over all values
of x must be 1:Any wave function satisfying this Equation is said to be normalized. Normalization is simply a statement that the particle exists at some point in space. Once the wave function for a particle is known, it is possible to calculate the average position at which you would expect to find the particle after many measurements. This average position is called the expectation value of x and is defined by the equation
Слайд 9The Wave Function
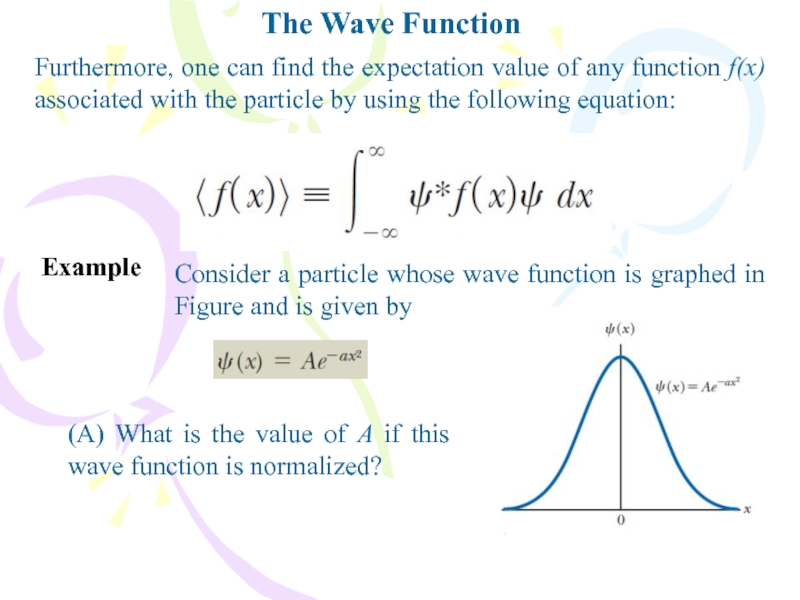
Furthermore, one can find the expectation value of
any function f(x) associated with the particle by using the
following equation:Example
Consider a particle whose wave function is graphed in Figure and is given by
(A) What is the value of A if this wave function is normalized?
Слайд 12(B) What is the expectation value of x for this
particle?
The Wave Function
SOLUTION
Evaluate the expectation value:
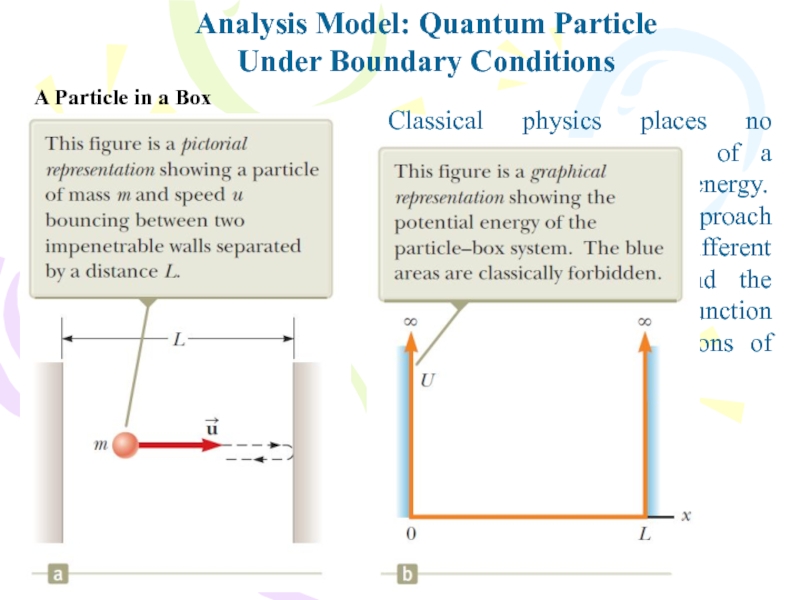
Слайд 14Classical physics places no restrictions on the values of a
particle’s momentum and energy. The quantum-mechanical approach to this problem
is quite different and requires that we find the appropriate wave function consistent with the conditions of the situation.Analysis Model: Quantum Particle
Under Boundary Conditions
A Particle in a Box
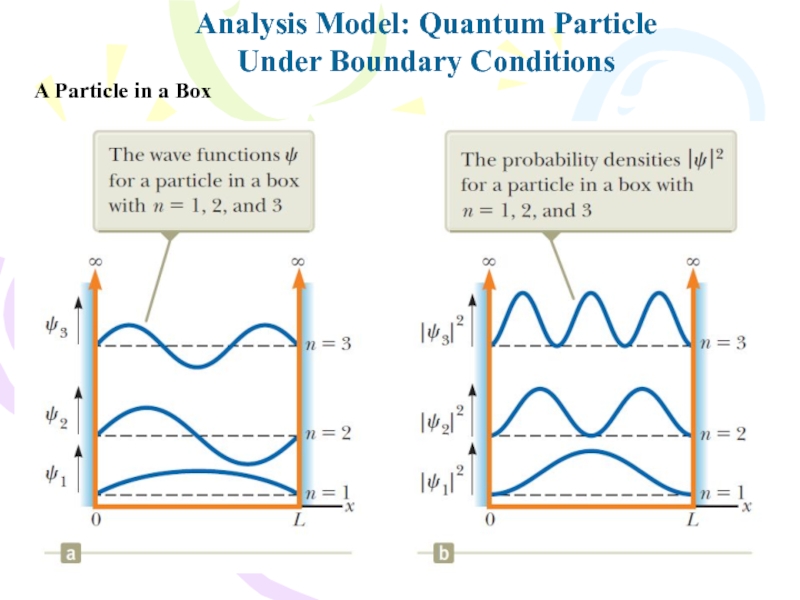
Слайд 15Analysis Model: Quantum Particle
Under Boundary Conditions
The wave function for a
particle in the box can be expressed as a real
sinusoidal function:Therefore, only certain wavelengths for the particle are allowed!
A Particle in a Box
Слайд 16Analysis Model: Quantum Particle
Under Boundary Conditions
Incorporating this Equation in previous
Equation gives
Normalizing this wave function shows that
Therefore, the normalized wave
function for the particle in a box isA Particle in a Box
Слайд 18Because the wavelengths of the particle are restricted by the
condition λ=2L/n, the magnitude of the momentum of the particle
is also restricted to specific values, which can be found from the expression for the de Broglie wavelengthAnalysis Model: Quantum Particle
Under Boundary Conditions
We have chosen the potential energy of the system to be zero when the particle is inside the box. Therefore, the energy of the system is simply the kinetic energy of the particle and the allowed values are given by
A Particle in a Box
Слайд 19Analysis Model: Quantum Particle
Under Boundary Conditions
Because the lowest energy of
the particle in a box is not zero, then, according
to quantum mechanics, the particle can never be at rest! The smallest energy it can have, corresponding to n=1, is called the ground-state energy. This result contradicts the classical viewpoint, in which E=0 is an acceptable state, as are all positive values of E.A Particle in a Box
Слайд 20Analysis Model: Quantum Particle
Under Boundary Conditions
Boundary Conditions on Particles in
General
In quantum mechanics, it is very common for particles to
be subject to boundary conditions. We therefore introduce a new analysis model, the quantum particle under boundary conditions. In many ways, this model is similar to the waves under boundary conditions model. In fact, the allowed wavelengths for the wave function of a particle in a box are identical in form to the allowed wavelengths for mechanical waves on a string fixed at both ends.The quantum particle under boundary conditions model differs in some ways from the waves under boundary conditions model:
• In most cases of quantum particles, the wave function is not a simple sinusoidal function like the wave function for waves on strings. Furthermore, the wave function for a quantum particle may be a complex function.
• For a quantum particle, frequency is related to energy through E =hf, so the quantized frequencies lead to quantized energies.
• There may be no stationary “nodes” associated with the wave function of a quantum particle under boundary conditions. Systems more complicated than the particle in a box have more complicated wave functions, and some boundary conditions may not lead to zeroes of the wave function at fixed points.
Слайд 21Analysis Model: Quantum Particle
Under Boundary Conditions
Boundary Conditions on Particles in
General
In general,
an interaction of a quantum particle with its
environment represents one or more boundary conditions, and, if the interaction restricts the particle to a finite region of space, results in quantization of the energy of the system.Слайд 22The Schrödinger Equation
Previously we discussed a wave equation for electromagnetic
radiation that follows from Maxwell’s equations. The waves associated with
particles also satisfy a wave equation. The wave equation for material particles is different from that associated with photons because material particles have a nonzero rest energy. The appropriate wave equation was developed by Schrödinger in 1926. In analyzing the behavior of a quantum system, the approach is to determine a solution to this equation and then apply the appropriate boundary conditions to the solution. This process yields the allowed wave functions and energy levels of the system under consideration. Proper manipulation of the wave function then enables one to calculate all measurable features of the system.Слайд 23The Schrödinger Equation
The Schrödinger equation as it applies to a
particle of mass m confined to moving along the x
axis and interacting with its environment through a potential energy function U(x) iswhere E is a constant equal to the total energy of the system (the particle and its environment). Because this equation is independent of time, it is commonly referred to as the time-independent Schrödinger equation.
Слайд 24The Schrödinger Equation
The Particle in a Box Revisited
Because of the
shape of the curve in Figure, the particle in a
box is sometimes said to be in a square well, where a well is an upward-facing region of the curve in a potential-energy diagram.Слайд 25The Schrödinger Equation
where A and B are constants that are
determined by the boundary and normalization conditions.
everywhere, which is not
a valid wave functionСлайд 26The Schrödinger Equation
Each value of the integer n corresponds to
a quantized energy that we call En. Solving for the
allowed energies En givesSubstituting the values of k in the wave function, the allowed wave functions are given by
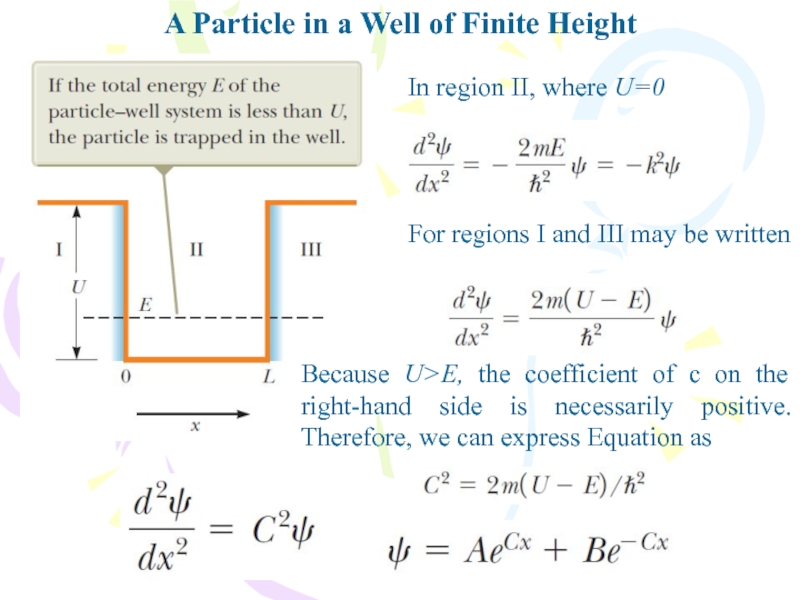
Слайд 27A Particle in a Well of Finite Height
In region II,
where U=0
For regions I and III may be written
Because U>E,
the coefficient of c on the right-hand side is necessarily positive. Therefore, we can express Equation asСлайд 30A Particle in a Well of Finite Height
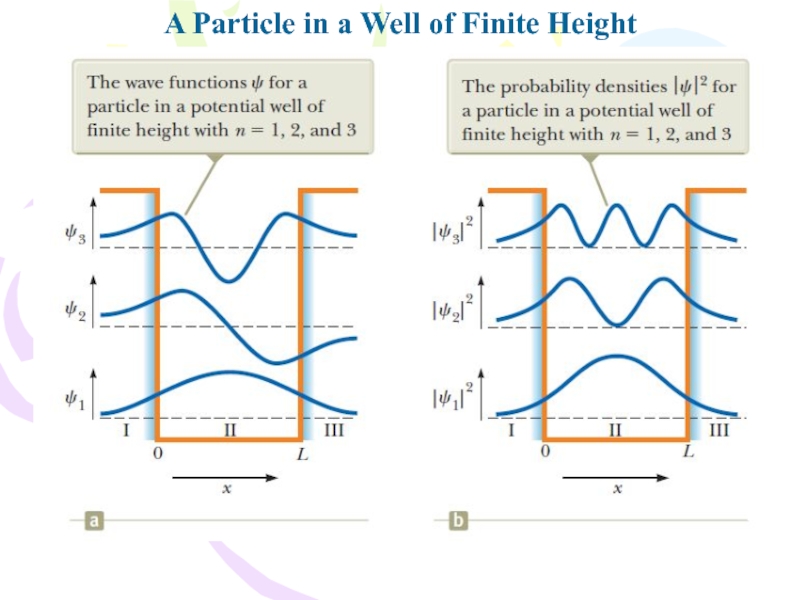
In evaluating the
complete wave function, we impose the following boundary conditions:
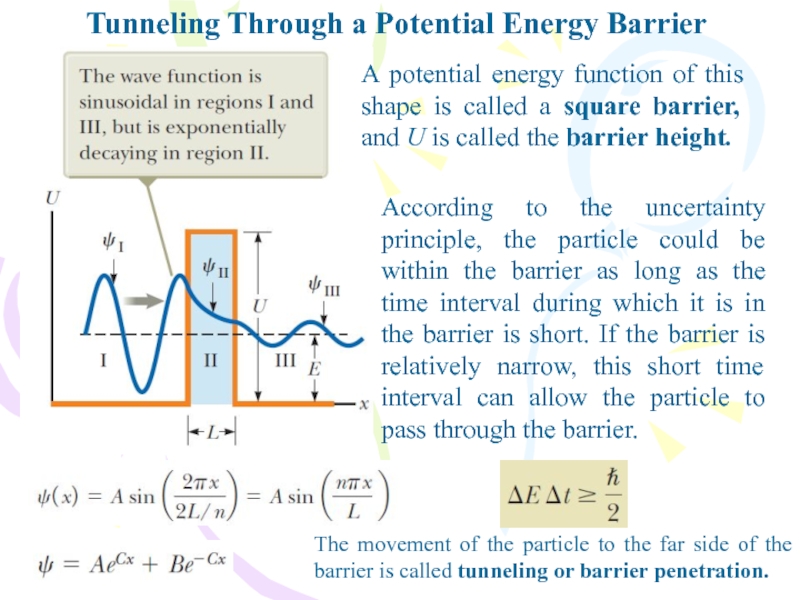
Слайд 31Tunneling Through a Potential Energy Barrier
A potential energy function of
this shape is called a square barrier, and U is
called the barrier height.According to the uncertainty principle, the particle could be within the barrier as long as the time interval during which it is in the barrier is short. If the barrier is relatively narrow, this short time interval can allow the particle to pass through the barrier.
The movement of the particle to the far side of the barrier is called tunneling or barrier penetration.
Слайд 32Tunneling Through a Potential Energy Barrier
The probability of tunneling can
be described with a transmission coefficient T and a reflection
coefficient R. The transmission coefficient represents the probability that the particle penetrates to the other side of the barrier, and the reflection coefficient is the probability that the particle is reflected by the barrier.This quantum model of barrier penetration shows that T can be nonzero. That the phenomenon of tunneling is observed experimentally provides further confidence in the principles of quantum physics.
Слайд 33The Simple Harmonic Oscillator
The potential energy of the system is
In
the classical model, any value of E is allowed, including
E=0, which is the total energy when the particle is at rest at x=0.where the angular frequency of vibration is
Слайд 34The Simple Harmonic Oscillator
Let’s investigate how the simple harmonic oscillator
is treated from a quantum point of view. The Schrödinger
equation for this problem isСлайд 35The Simple Harmonic Oscillator
It turns out that the solution we
have guessed corresponds to the ground state of the system,
which has an energyThe energy levels of a harmonic oscillator are quantized as we would expect because the oscillating particle is bound to stay near x=0. The energy of a state having an arbitrary quantum number n is