Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Содержание
- 1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- 2. Уравнение линии на плоскости Линия – это
- 3. 1.Задана линия l как множество точек плоскости,
- 4. Уравнение прямой на плоскости по точке и
- 5. М0(x0,y0) - точка на прямой,
- 6. Пример 1.Написать уравнение прямой, проходящей через точку
- 7. Решение.=>Вектор можно
- 8. Пример 3.Написать уравнение прямой, проходящей через точку
- 9. Общее уравнение прямой на плоскостиНа плоскости
- 10. Пример 1.1. Построить прямую 3х-2у+6=0. 2.Проверить, лежат
- 11. Положим в уравнении у=0, тогда: 3х+6=0. Отсюда:
- 12. 2. Проверим, проходит ли прямая через точку
- 13. Частные случаи общего уравнения прямой на плоскостиОбщее
- 14. 2. Пусть В=0, А0, С0. В этом
- 15. 3. Пусть С=0, А0, В0. Уравнение прямой
- 16. 4. Пусть А=С=О, ВО. В этом случае
- 17. Уравнение прямой с угловым коэффициентом Общее уравнение
- 18. Уравнение пучка прямых на плоскости Рассмотрим уравнение
- 19. Пример: Написать уравнение прямой, проходящей через точку
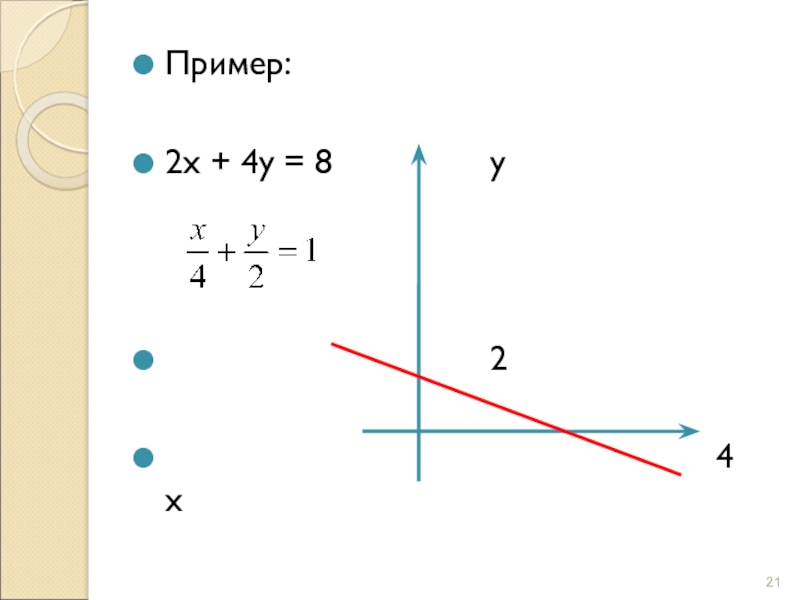
- 20. Уравнение прямой в отрезках на осяхОбщее уравнение прямой:Ах+Ву+С=0 или Ах+Ву=-Сили
- 21. Пример:2х + 4у = 8
- 22. Уравнение прямой на плоскости по точке и
- 23. Вектор
- 24. Пример 1: Написать уравнение прямой, проходящей через
- 25. Угол между двумя прямыми на плоскости. Условие
- 26. Угол между двумя прямыми равен углу между
- 27. Пример 1: Найти угол между прямыми 3х+у-5=0
- 28. Пример 2: Найти угол между прямыми 2х+6у+1=0
- 29. Условие параллельности прямых совпадает с условием коллинеарности
- 30. Условие параллельности и перпендикулярности прямых, если они
- 31. Из условия А1А2 + В1В2=0
- 32. Пример: Написать уравнение прямой, проходящей через точку
- 33. Точка пересечения прямых Прямые заданы общими уравнениями:I:
- 34. Пример:Найти точку пересечения прямых 5х-3у-15=0 и х+2у-3=0.Решение:Решаем
- 35. Скачать презентанцию
Уравнение линии на плоскости Линия – это множество точек плоскости, обладающих определенным свойством. Уравнением линии l называется уравнение вида F(x,y)=0, которому удовлетворяют координаты всех точек, лежащих на линии l, и не
Слайды и текст этой презентации
Слайд 1АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Аналитическая геометрия - это раздел курса высшей математики, в
котором изучаются свойства геометрических объектов алгебраическими способами.
Слайд 2Уравнение линии на плоскости
Линия – это множество точек плоскости, обладающих
определенным свойством. Уравнением линии l называется уравнение вида F(x,y)=0, которому
удовлетворяют координаты всех точек, лежащих на линии l, и не удовлетворяют координаты ни одной точки, не лежащей на этой линии.Аналитическая геометрия на плоскости ставит перед собой две основные задачи:
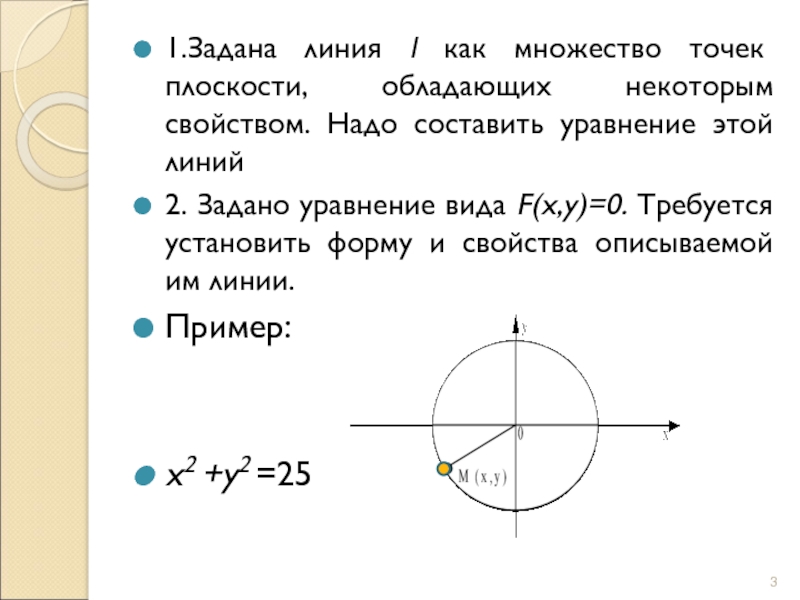
Слайд 31.Задана линия l как множество точек плоскости, обладающих некоторым свойством.
Надо составить уравнение этой линий
2. Задано уравнение вида F(x,y)=0. Требуется
установить форму и свойства описываемой им линии.Пример:
x2 +y2 =25
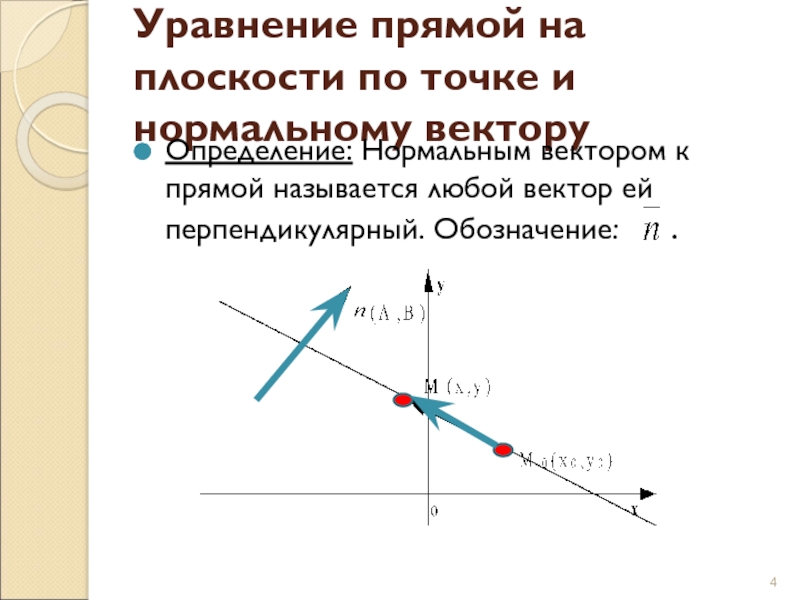
Слайд 4Уравнение прямой на плоскости по точке и нормальному вектору
Определение: Нормальным
вектором к прямой называется любой вектор ей перпендикулярный. Обозначение:
.
Слайд 5М0(x0,y0) - точка на прямой,
- нормальный вектор этой прямой
. (А и В одновременно нулю не равны). M(x,y) – произвольная точка рассматриваемой прямой. Введем в рассмотрение векторВектор и вектор - ортогональны => , или:
А(х-х0)+В(у-у0)=0 (1)
Слайд 6Пример 1.
Написать уравнение прямой, проходящей через точку М(1,-3) и имеющую
нормальный вектор
Решение. Из уравнения (1) следует:
2(х-1)+5(у+3)=0
или 2х+5y+13=0.Пример 2.
Даны вершины треугольника АВС: А(1,2);
В(-3,5);C(1,4). Написать уравнение высоты HA, опущенной из вершины А.
Слайд 7Решение.
=>
Вектор можно принять за нормальный
вектор с координатами (4,-1).
Тогда уравнение высоты:
4(х-1)-1(у-2)=0, или 4х-у-2=0.
Слайд 8Пример 3.
Написать уравнение прямой, проходящей через точку М(-4,2) и имеющую
нормальный вектор
.Решение. Из уравнения (1) следует:
0(х+4)-3(у-2)=0
или у=2.
Слайд 9 Общее уравнение прямой на плоскости
На плоскости XOY уравнение Ах+Ву+С=0
определяет прямую линию, при условии, что А и В одновременно
не равны нулю. Раскроем скобки в (1):Ах-Ах0+Ву-Ву0=0.
Обозначим - Ах0-Ву0=С. Тогда уравнение (1) приведется в виду:
Ах+Ву+С=0 (2) - общее уравнение прямой на плоскости. Коэффициенты А и В - координаты нормального вектора этой прямой.
Слайд 10Пример 1.
1. Построить прямую 3х-2у+6=0. 2.Проверить, лежат ли точки М1(1,2)
и
М2(-4,-3) на этой прямой.
3. Найти нормальный вектор этой
прямой.Решение. 1. Чтобы построить прямую, найдем две точки, лежащие на ней и проведем через них прямую линию.
Положим в уравнении х=0, тогда –2у+6=0. Отсюда: у=3. Таким образом, точка А с координатами (0,3) лежит на прямой.
Слайд 11Положим в уравнении у=0, тогда: 3х+6=0. Отсюда: х=-2. Нашли вторую
точку, лежащую на прямой – В(-2,0). Откладываем их на осях
координат и строим прямую l.
Слайд 122. Проверим, проходит ли прямая через точку М1. Подставим координаты
точки в уравнение прямой. Получим: 3·1-2·2+60. Координаты точки М1 не
удовлетворяют уравнению прямой l, => точка М1 не лежит на данной прямой.Подставим координаты точки М2 в уравнение прямой. Получаем: 0=0, => точка М2 лежит на прямой.
Координаты нормального вектора равны коэффициентам при х и у в общем уравнении прямой.
Слайд 13Частные случаи общего уравнения прямой на плоскости
Общее уравнение прямой: Ах+Ву+С=0
1. Пусть А=0, В0, С0. Уравнение примет вид: Ву+С=0 или
у=b, гдеНормальный вектор этой прямой
перпендикулярен оси ОХ
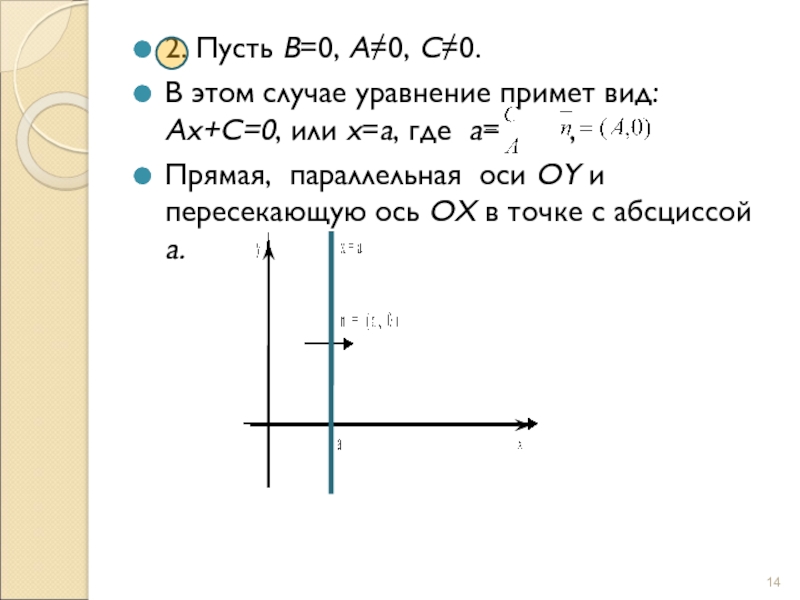
Слайд 142. Пусть В=0, А0, С0.
В этом случае уравнение примет
вид: Ах+С=0, или х=а, где а= ,
Прямая,
параллельная оси OY и пересекающую ось OX в точке с абсциссой а. =
.
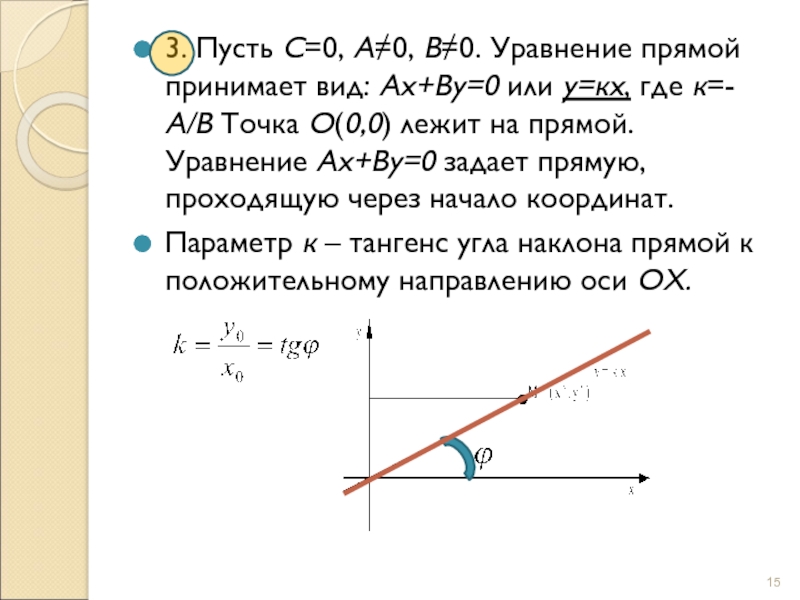
Слайд 153. Пусть С=0, А0, В0. Уравнение прямой принимает вид: Ах+Ву=0
или у=кх, где к=-А/В Точка О(0,0) лежит на прямой. Уравнение
Ах+Ву=0 задает прямую, проходящую через начало координат.Параметр к – тангенс угла наклона прямой к положительному направлению оси ОХ.
Слайд 164. Пусть А=С=О, ВО. В этом случае уравнение прямой принимает
вид: Ву=0 или у=0. Это уравнение выражает прямую, одновременно параллельную
оси ОХ и проходящую через начало координат. Уравнение у=0 есть уравнение координатной оси ОХ.Аналогично, уравнение х=0 представляет собой уравнение координатной оси ОУ
Слайд 17Уравнение прямой с угловым коэффициентом
Общее уравнение прямой на плоскости: Ах+Ву+С=0.
Пусть В0, (прямая не параллельна оси ординат). Тогда
у= . угловой коэффициент прямой к= -А/В , параметр b=-С/В - ордината точки пересечения прямой с осью ОУ. Уравнение записано в виде: у=кх+b. Оно называется уравнением прямой с угловым коэффициентом.
Слайд 18Уравнение пучка прямых на плоскости
Рассмотрим уравнение :
А(х-х0) + В(у-у0) = 0.
Пусть
В≠0, то есть прямая не параллельна оси ординат. Тогда у-у0 = к(х-х0),где к=-А/В – угловой коэффициент прямой. Множество всех прямых на плоскости, проходящих через данную точку (х0,у0), называется пучком прямых с центром в этой точке. Если к фиксировано, получим уравнение прямой по точке и угловому коэффициенту.
Слайд 19Пример:
Написать уравнение прямой, проходящей через точку М0(3,-1) и образующей
с осью ОХ угол 450.
Решение: Воспользуемся уравнением
у-у0 = к(х-х0).
Здесь ,х0=3, у0=-1. Следовательно, получаем:
у+1=1(х-3) или х-у-4=0
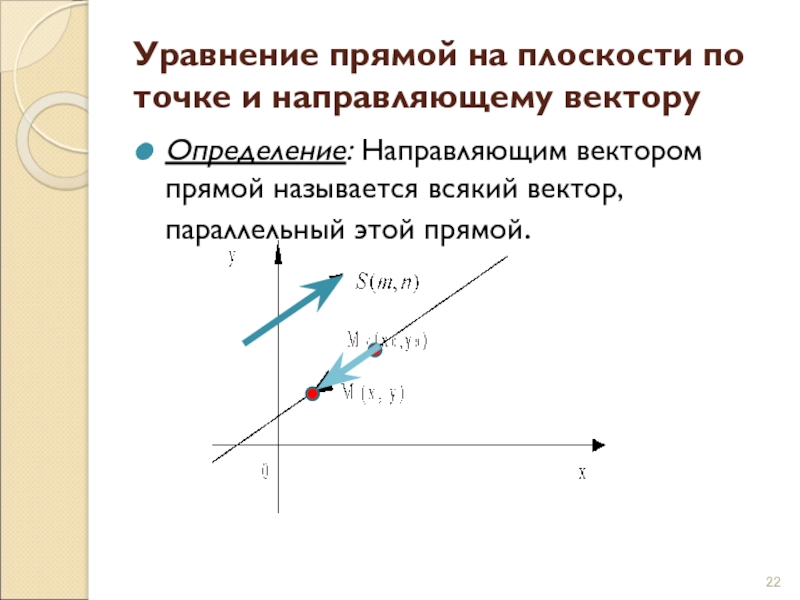
Слайд 22Уравнение прямой на плоскости по точке и направляющему вектору
Определение: Направляющим
вектором прямой называется всякий вектор, параллельный этой прямой.
Слайд 23Вектор (х-х0, у-у0)
будет параллелен вектору =(m,n). Следовательно,
(условие коллинеарности
векторов). Это равенство будет справедливо только для тех точек, которые лежат на прямой => уравнение прямой на плоскости по точке и направляющему вектору или каноническое уравнение прямой.
Слайд 24Пример 1: Написать уравнение прямой, проходящей через точку М0(-2,0), параллельно
вектору
Решение:
Из уравнения следует:
или
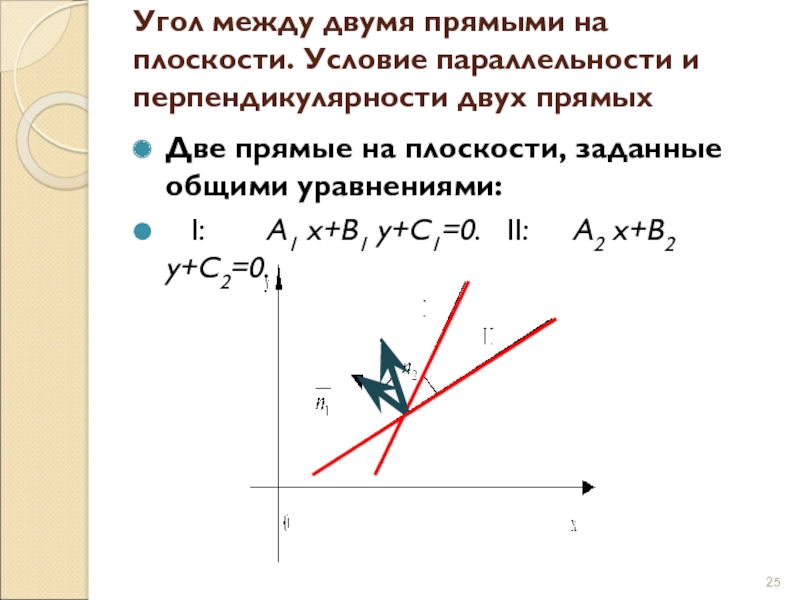
х+3у+2=0
Слайд 25Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности
двух прямых
Две прямые на плоскости, заданные общими уравнениями:
I:
А1 х+В1 у+С1=0. II: А2 х+В2 у+С2=0.
Слайд 26Угол между двумя прямыми равен углу между нормальными векторами этих
прямых:
иCos φ=
Формула определяет один из углов между прямыми, второй угол равен π-φ
Слайд 27Пример 1:
Найти угол между прямыми 3х+у-5=0 и 2х-у+1=0.
Решение:
По формуле имеем:
Cosφ=
=один из углов равен π/4, другой 3π/4.
Слайд 28Пример 2:
Найти угол между прямыми 2х+6у+1=0 и 9х-3у+8=0.
Решение: По
формуле имеем:
Cosφ =
=OОдин из углов равен π/2, другой 3π/2, прямые перпендикулярны.
Слайд 29Условие параллельности прямых совпадает с условием коллинеарности их нормальных векторов:
Условие перпендикулярности прямых совпадает с условием ортогональности их нормальных векторов,
следовательно, оно имеет вид:А1А2 + В1В2=0
Слайд 30Условие параллельности и перпендикулярности прямых, если они заданы уравнениями с
угловыми коэффициентами.
I: y=k1x+b1 ;
II: y=k2x+b2
Выразим предыдущие условия через
угловые коэффициенты прямых:=>
Слайд 31Из условия А1А2 + В1В2=0 =>
Или
Итак, прямые
параллельны: к1=к2
Прямые перпендикулярны: угловые коэффициенты обратны по величине и
противоположны по знаку . 
Слайд 32Пример: Написать уравнение прямой, проходящей через точку М(5, -1) параллельно
прямой у=2.
Решение: Так как прямые параллельны, то к1=к2, следовательно, к1=0.
Получаем: у+1=0(х-5), или у=-1.Пример : Написать уравнение прямой, проходящей через точку М(5, -1) перпендикулярно прямой у=2.
Решение: Так как к2=0,, то прямая у=2 параллельна оси ОХ. Искомая прямая перпендикулярна оси ОХ и проходит через точку М(5, -1). Уравнение такой прямой: х=5
Слайд 33Точка пересечения прямых
Прямые заданы общими уравнениями:
I: А1
х+В1 у+С1=0. II: А2 х+В2 у+С2=0.
Пусть точка М0(х0,у0)
точка пересечения прямых. Тогда ее координаты х0,у0 удовлетворяют и уравнению I и уравнению II. Следовательно, координаты этой точки являются решением системы уравнений:
Слайд 34Пример:
Найти точку пересечения прямых 5х-3у-15=0 и х+2у-3=0.
Решение:
Решаем совместно систему уравнений
получаем:
х=3, у=0. Таким образом, точка пересечения прямых имеет координаты: М0(3,0).
