Анализ начальных участков изотерм адсорбции

применимость уравнения БЭТ, cравнительный метод, теория объемного заполнения микропор Дубинина

(ТОЗМ), распределение объема микропор по размерам.

Начальные участки ИА (до начала капиллярной конденсации) используются для определения удельной поверхности А, объема микропор Vµ и их распределения

основе работ М.М.Дубинина)
Микропоры – эффективный размер Н  2 нм
Мезопоры

– размер 2 нмМакропоры – Н > 50 нм

Эффективный размер Н – диаметр наибольшей окружности, которая может быть вписана в плоское сечение поры произвольной формы (эфф. размер полости – по максим. диаметру вписанной сферы)

Эта классификация основана на особенностях адсорбции
в порах разных размеров

расположенных стенок пор. Поэтому такие поры заполняются при малых значениях

Р/Р0 с повышенными Qадс

Классификация адсорбентов по размерам пор

большой кривизны поверхности)-
капиллярная конденсация, обычно - с характерным гистерезисом
Область

капиллярной
конденсации с
гистерезисом

и полимолекулярная адсорбция
Макропоры

БЭТ (обычно – область Р/Р0 0.05- 0.30).
С момента рождения

(1938 г) этот метод критикуют, модифицируют и тем не менее он остается наиболее широко использу-емым методом расчета удельной поверхности по адсорбционным данным

молекулярных посадочных площадок i в заполненном монослое, как и постоянство

принятого значения N2 = 0.162 нм2

АБЭТ = amNA

a

P/P0

модель БЭТ предполагает:

-энергетическую однородность поверхности,

-отсутствие взаимодействия G/G в слое ????

-полимолекулярную адсорбцию до завер-шения образования монослоя

но

не использующих значения ;

Поэтому БЭТ с современной точки зрения

- это не обосно-ванная теория адсорбции на реальной неоднородной поверхности, а модель, дающая простое аналитическое уравнение.
Но отличия АБЭТ от результатов независимых измерений на гладких поверхностях макропористых или непористых систем обычно не превышают 20-30% относ.

Это рождает проблемы:

значений , которые необхо-димы для перехода от емкости монослоя аm

к поверхности А
Удельная поверхность
А = аmNA
где NA –число Авогадро

без ?
Альтернатива – отказаться от  и определять уд.

поверхность А по области полимолекуляр-ной адсорбции, менее чувствительной к природе поверхности адсорбента, где опреде-ляющим становится взаимодействие G/G.
По результатам прецизионных калориметри-ческих исследований, для этого надо нанести на поверхность ~1.2 монослоя адсорбата (G)

Проблема БЭТ

адсорбции N2 на крупно-
пористых системах разной
химической природы в области

Р/Р0 > 0.1 - 0.2 удовлетворительно
описываются общим графиком,

если нормировать ИА как а/АБЭТ

Это подтверждает относительно слабое влияние природы поверхности на полимолекулярную адсорбцию на поверхности мезо- и макропор.
ИА в этой области назвали стандартными (СИА).

для разных систем.
Использовались разные способы нормировки изотерм адсорбции:
 = а/А

(мкМоль/м2) – А.В. Киселев
t (нм) = avm/A- (где vm – мольный объем)- де Бур и т.д.
В настоящее время за рубежом наиболее популярна нормировка Синга
s = /0.4, где 0.4 – уд. адсорбция при Р/Ро = 0.4)
но все эти нормировки линейно взаимосвязаны, например, t = vm

в области полимолекулярной адсорбции, измеренных в идентичных условиях на различных

макро- и мезопористых системах, соответствует условию

мезопорах приводит к дополнительной адсорбции. Адсорбция в микропорах происходит только

в начальной области изотермы и обычно завершается до образования монослоя на остальной поверхности, а капиллярная конденсация начинается при относи-тельно высоких Р/Р0 в области полимолек. адсорбции.
На изотерме адсорбции обычно существует достаточ-но протяженная область полимолекулярной адсорб-ции после завершения адсорбции в микропорах до начала капиллярной конденсации



зависим от БЭТ, т.к. поверхность стандарта сравнения может быть определена

независимым от БЭТ методом (электронная микроскопия на модельных системах и др).
Постоянство значений функции α(Р/Р0) наблюдается в области полимолекулярной адсорбции после образования монослоя на всей поверхности до начала заметного дополнительного вклада капиллярной конденсации.

системе N2/СН3ОН/ГС
m – степень покрытия поверхности модификато-ром, стандарт сравнения –

ИА на немодифицирован-ной ГС (исходной)
В области полимолеку-лярной адсорбции графи-ки параллельны, т.е. А = Соnst и не зависит от наличия модификатора

данные Синга)
Стандарт сравнения – СИА N2 на непористых системах

0.1)

возможностях Теории Объемного Заполнения Микропор (ТОЗМ), которая развивается с 1947

г российской школой академика М.М. Дубинина, а в последние десятилетия – и во многих других странах.
Первоначально ТОЗМ была развита для описания ИА в активных углях с характерной для них структурой щелевидных пор, позже была распространена на другие микропористые системы.

потенциал (дифференциальная мольная работа переноса моля газа в адсорбированное жидкофазное

состояние)
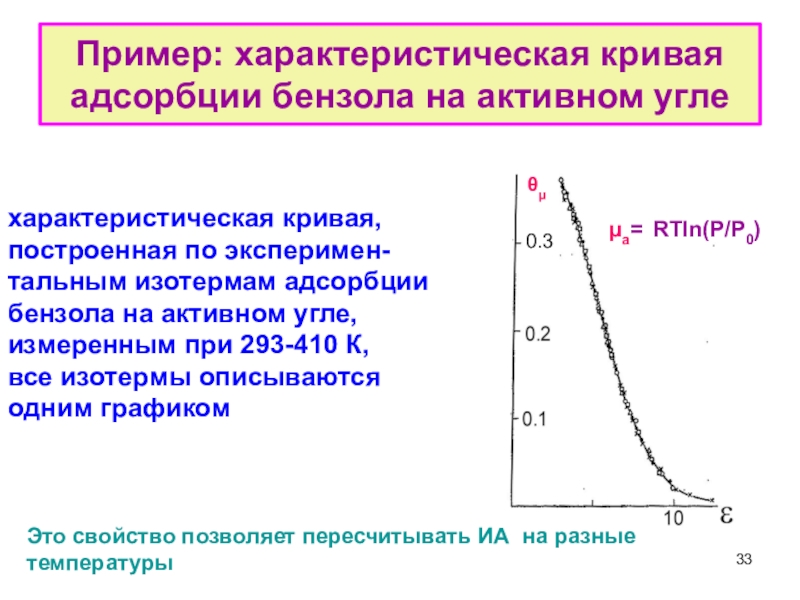
µа= µ = RTln(P/P0)
Степень заполнения объема W0 – функция свойств адсорбата и адсорбента в широком температурном диапазоне выражается уравнениями типа
µ = W/W0 = exp [(- µа/E0)n].
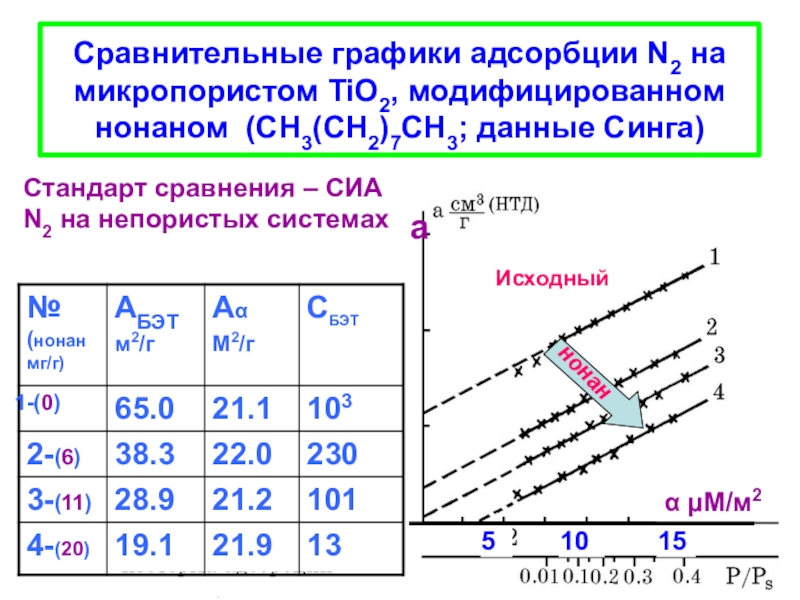
 - коэффициент аффинности (подобия), характеризующий адсорбционные свойства использованного адсорбата относительно стандартного (N2 или C6H6);
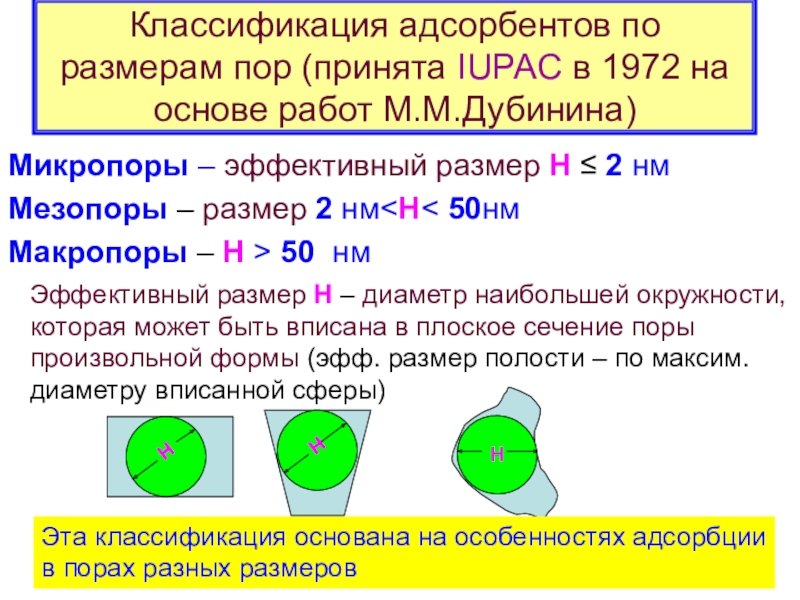
Е0 – средняя характеристическая энергия адсорбции для данного адсорбента, возрастающая с уменьшением средних размеров микропор, для щелевидных пор в активных углях полуширина пор X  12/Е0 (где X - нм, Е0 - кдж/моль). Существуют и другие аппроксимации связи Х и Е0.

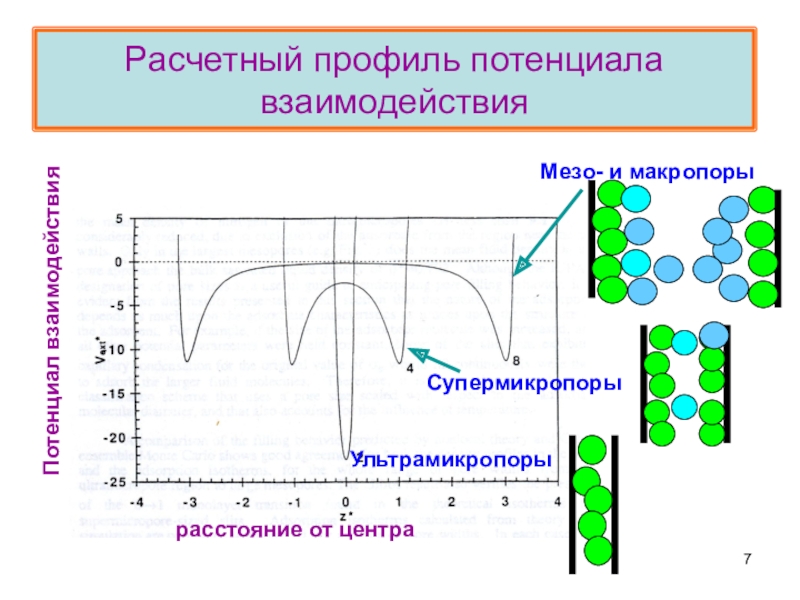
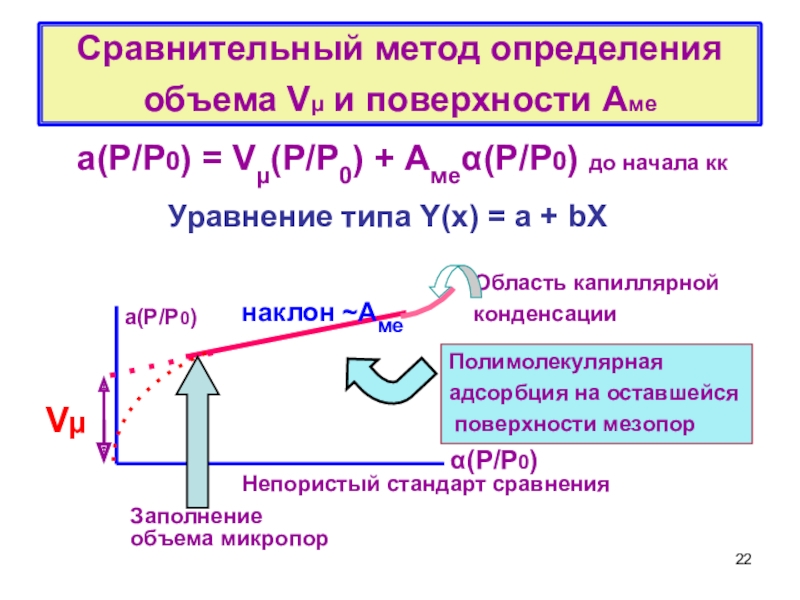
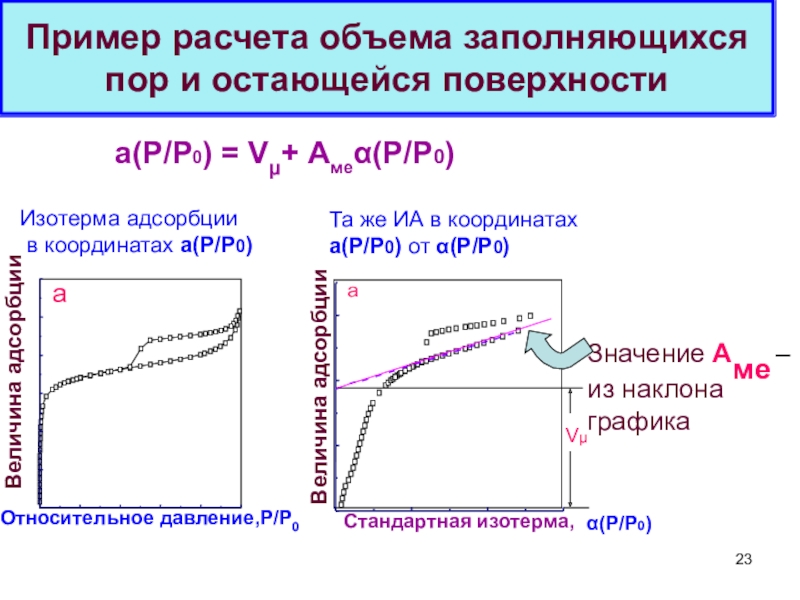
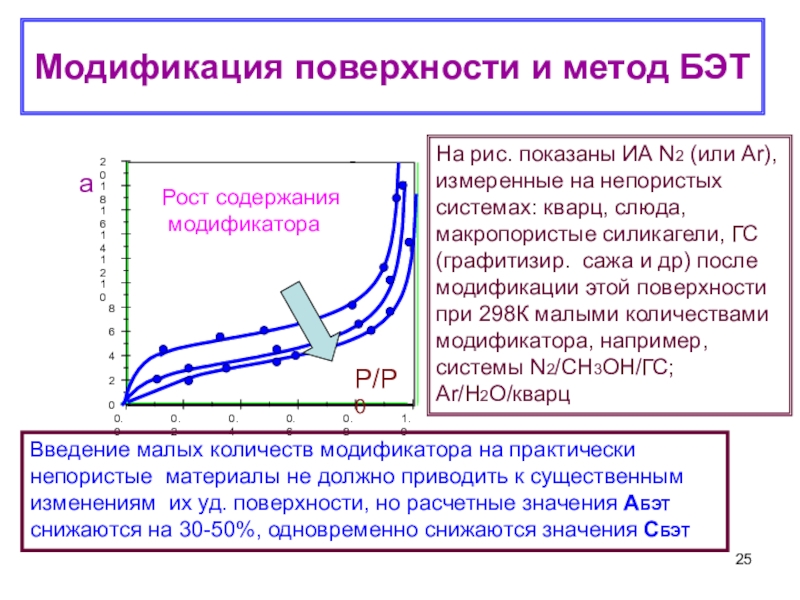
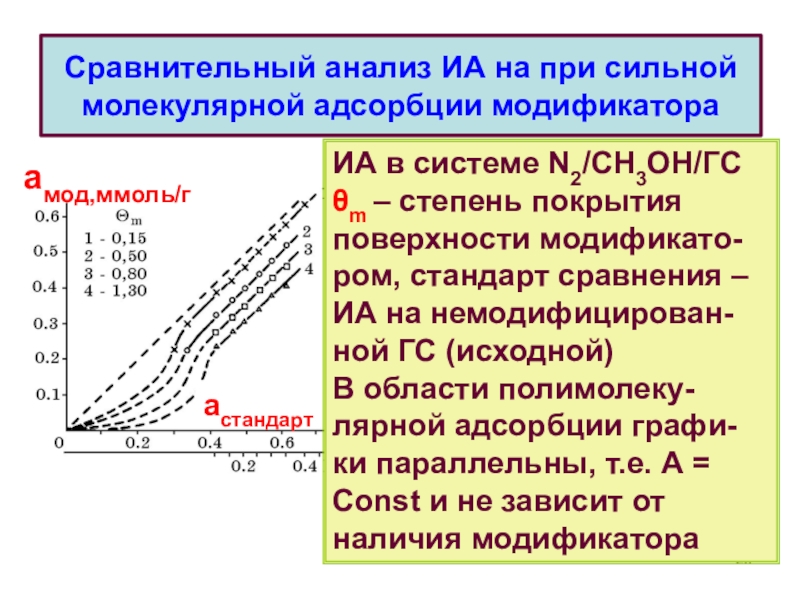
Теория объемного заполнения микропор (ТОЗМ) – школа М.М. Дубинина

ИА – практическая независимость функции µ = µ(µа) = µ(RTln(P/P0))

от температуры.
µа = µ(RTln(P/P0))-адсорбционный потенциал.
График функции µ от µа называют характеристической кривой для данного адсорбента.

–Радушкевича, предложенным в 1947 г.
µ = W/W0 = exp

[(-µа/E0)2]
называемым уравнением ДР.
В этом уравнении Е0 и W0 характеризуют адсорбент, - адсорбат.
Уравнение ДР соответствует статистически нормальному (гауссовскому) распределению микропор с разным адс. потенциалом µа.

стандартного (N2 или C6H6) адсорбатов.
Парахор – не зависящий от

Т параметр, равный ж1/4/(ж - пара), где ж - поверхностное натяжение жидкости
(иногда – отношение мольных объемов и др. эмпирические корреляции).

Коэффициент аффинности в ТОЗМ

координатах уравнения ДР с учетом коэффициентов аффинности 

в координатах ДР
W/W0 = exp [(-µа/E0)2], где µа= RTln(P0/P)

привело к более общему уравнению ДА (Дубинин-Астахов) :
µ =

W/W0 = exp [(-µа/E0)n].
n (=1-5) –параметр, характеризующий свойства адсорбента (рост n – сужение распределения размеров пор).
Для супермикропористых углей n =1;
Для цеолитов n =4-5.
Такой вид уравнения соответствует статистике Вейбула (Weibull), где допускаются ассимметричные распределения, а нормальное распределение - частный случай.