Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Анализ работы импульсного регулятора сопротивления
Содержание
- 1. Анализ работы импульсного регулятора сопротивления
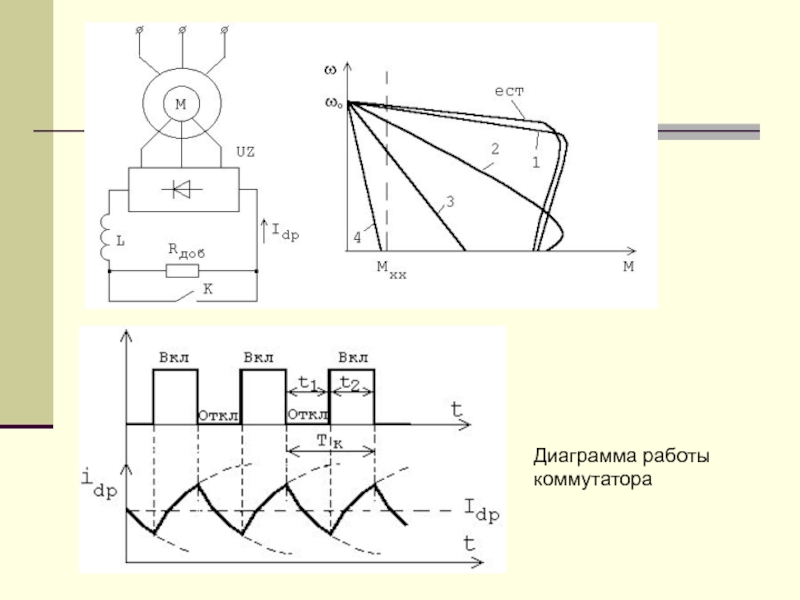
- 2. Диаграмма работы коммутатора
- 3. Среднее значение выпрямленного тока ротора Idp, которое
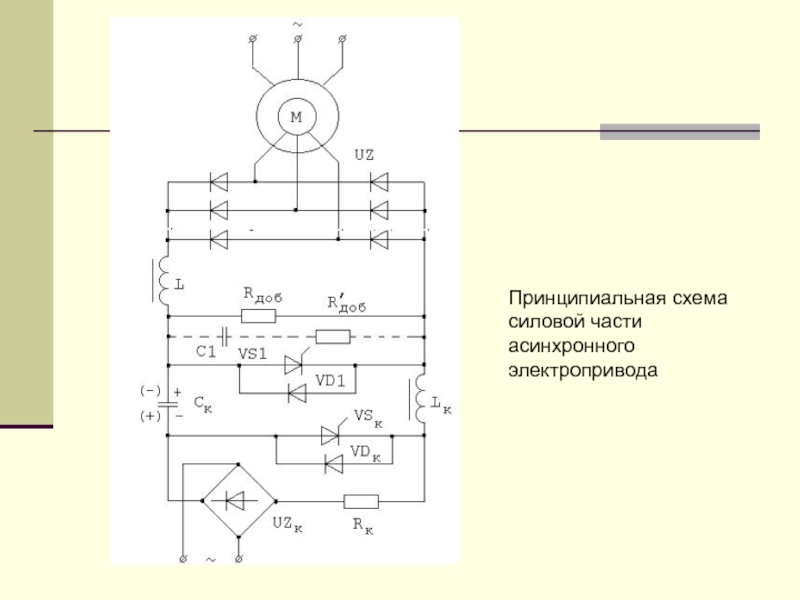
- 4. Принципиальная схема силовой части асинхронного электропривода
- 5. Среднее значение импульсного регулируемого сопротивления Rd линейно
- 6. Слайд 6
- 7. Диаграммы напряжений отражающие работу схемы показаны ниже
- 8. Регулировочная характеристика коммутатора имеет вид, Коэффициент передачи
- 9. Анализ статических характеристик замкнутой системы
- 10. Слайд 10
- 11. на вход усилителя А2, формирующего сигнал обратной
- 12. Ке⋅ Uе = Кс⋅ ωо; Кн= Кс⋅ (ωо/Edo); КТ
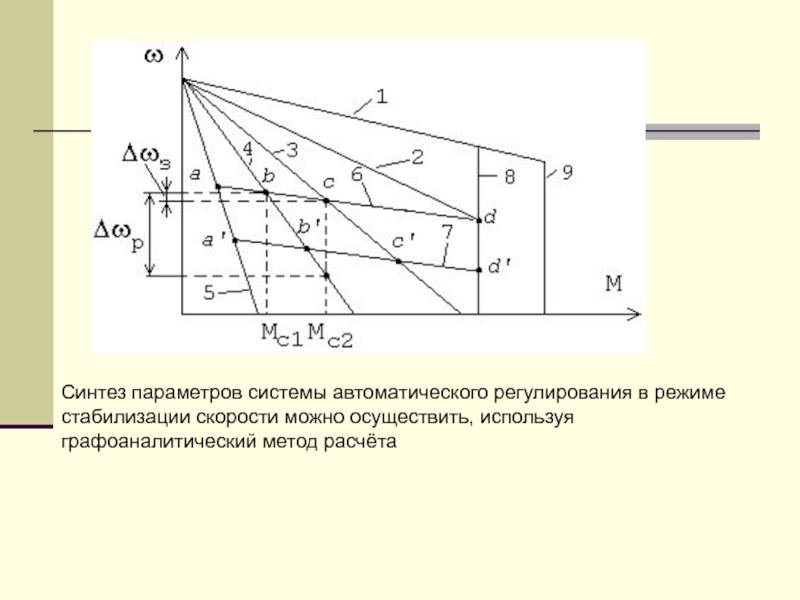
- 13. Синтез параметров системы автоматического регулирования в режиме стабилизации скорости можно осуществить, используя графоаналитический метод расчёта
- 14. Ку (Кзс⋅Uзс – Кос⋅Кс⋅ωа)= 0; Ку (Кзс⋅Uзс
- 15. В тех случаях, когда момент нагрузки на
- 16. Динамические характеристики системы с импульсным регуляторомдифференциальные
- 17. Составить структурную схему по этим уравнениям невозможно
- 18. Линеаризировать нелинейную зависимость выпрямленного тока ротора id
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1АСИХРОННЫЙ ЭЛЕКТРОПРИВОД С ИМПУЛЬСНЫМ РЕГУЛИРОВАНИЕМ СОПРОТИВЛЕНИЯ РОТОРНОЙ ЦЕПИ.
Анализ работы
импульсного регулятора сопротивления
Слайд 3Среднее значение выпрямленного тока ротора Idp, которое определяет момент двигателя
при данном скольжении, зависит от скважности (относительной продолжительности включения) процесса
коммутации ключа К ε = t1 /Tк.Работа тиристорного коммутатора происходит следующим образом:
Открытому состоянию тиристора VS1 соответствует механическая характеристика 1 на рис. 1.б, закрытому – 4. Соотношение открытого и закрытого состояния определяет скважность процесса коммутации и вид механической характеристики. При постоянной скважности 0 < ε < 1 получается характеристики типа 2 или 3 на рис..1,б, причём ε 2 > ε 3.
Слайд 5Среднее значение импульсного регулируемого сопротивления Rd линейно зависит от скважности
Rd=Rдоб ⋅(1- ε)
Idp=Edo⋅S/(Rэ+Rd)
отсюда
Rэ=(S⋅m⋅Xд/2⋅π)+2⋅Rд
где
где .,Хд
= Х2 + Х1' Rд = R2+R1'
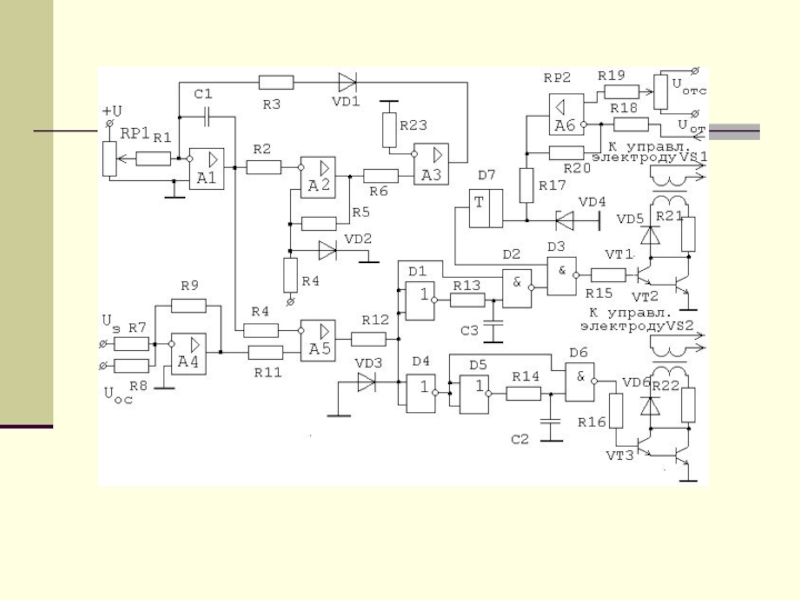
Один из вариантов схемы управления тиристорным коммутатором приведён на рис.
Слайд 8Регулировочная характеристика коммутатора имеет вид,
Коэффициент передачи звена может быть
подсчитан по выражению
Если учесть дискретность управления системы управления коммутатором, передаточная
функция коммутатора может быть описана выражениемWк(p) = Kу (ехр) -τу р,
Слайд 9Анализ статических характеристик замкнутой системы
регулирования скорости.
Вариант замкнутой системы
регулирования скорости с суммирующим
усилителем приведён на рис
Выделение сигнала
Uос осуществляется косвенным образом путём измерения выпрямленного напряжения Ud и выпрямленного тока Id.Пропорциональность выходного напряжения Uос усилителя А2 текущему значению скорости базируется на следующем
Еdo⋅ S = Ud + Id ⋅ Rэ
Тогда
S = (Ud + Id⋅Rэ)/Edo
ω = ωо(1– S )= (ωо/Edo)[Edo – (Ud + Id ⋅ Rэ)]
Слайд 11на вход усилителя А2, формирующего сигнал обратной связи по скорости,
в соответствии с уравнением подаются три сигнала
Напряжение на выходе
А2 Uос = Ке⋅ Uе – [R2/(R1+R2)]КU ⋅ Ud – Rш⋅ КI ⋅ Id
или Uос = Кс⋅ ω = Ке⋅ Uе – Кн⋅ Ud – КТ⋅ Id
где Ке = R11/R16; КU = R11/(R13+R14); КI = R11/(R12+R15)
Кн = [R2/(R1+R2)]⋅КU; КТ = Rш⋅ КI
Для нахождения соотношений между коэффициентами обратных связей и параметрами схемы умножим почленно выражение для ω на Кс
Кс⋅ωо – Кс⋅ (ωо/Edo)⋅ Ud – Кс (ωо/Edo)⋅ Rэ⋅ Id = Ке⋅ Uе – Кн⋅ Ud – КТ⋅ Id
Отсюда получим
Слайд 12Ке⋅ Uе = Кс⋅ ωо; Кн= Кс⋅ (ωо/Edo); КТ = Кс⋅ (ωо/Edo)⋅
Rэ
Для анализа работы системы регулирования запишем уравнения, характеризующие процессы
в цепи управления коммутатором Uу= Кзс⋅ Uз – Кос⋅ Кс ω
где Кзс=R6/(R3+R4); Кос = R6/R5
ε = Ку⋅ Uу = Ку⋅ (Кзс⋅ Uзс – Кос⋅ Кс⋅ ω)
В режиме стабилизации скорости схема работает следующим образом
Слайд 13
Синтез параметров системы автоматического регулирования в режиме стабилизации скорости можно
осуществить, используя графоаналитический метод расчёта
Слайд 14Ку (Кзс⋅Uзс – Кос⋅Кс⋅ωа)= 0;
Ку (Кзс⋅Uзс – Кос⋅Кс ωd
)= ε2
Вычитая из 2 1 получим
Ку⋅Кос⋅Кс = ε2/(ωа–ωd )=
ε2 /Δ ωз при известных значениях Ку, Кос и Кс
Uзс = (Кос/Кзс)Кс ωа
Уравнение механической характеристики замкнутой системы регулирования
Слайд 15В тех случаях, когда момент нагрузки на валу двигателя достигнет
больших значений, вступит в работу узел токоограничения. Регулировочная характеристика узла
токоограничения изображена на рисПри превышении сигналом обратной связи Uот напряжения отсечки Uотс на величину ΔU, то есть когда
(R17/R10)⋅Uот – Uотс ≥ ΔU
параметры узла токоограничения можно определить из
[Rш /(R15+R10)] Id оТс=UоТс/R17
Слайд 16Динамические характеристики системы с импульсным
регулятором
дифференциальные уравнения, записанные для каждого
узла системы.
КА1 (Uзс – Кс⋅ ω) = Uу;
Ку
⋅ Uу ⋅ехр–τу⋅р = ε;
Слайд 17Составить структурную схему по этим уравнениям невозможно из-за наличия нескольких
нелинейностей, обусловленных зависимостью эквивалентного сопротивления ротора от скольжения, а также
от относительной продолжительности включенияКроме того, электромагнитный момент двигателя нелинейно зависит от выпрямленного тока id
Для практических расчётов можно принять Rэ при среднем значении скольжения Sср для заданного диапазона регулирования скорости
Нелинейную зависимость момента М от id можно линеаризировать, если коэффициент между моментом и током в уравнении определить по средней для данного привода нагрузке:
Слайд 18Линеаризировать нелинейную зависимость выпрямленного тока ротора id от относительной продолжительности
включения обычными методами не удаётся. Однако если учесть, что используемая
в системе отрицательная связь по току id в конечном итоге обеспечивает стабилизацию (релейное регулирование) момента двигателя, то приняв за величину инерционности контура релейного регулирования момента электромагнитную постоянную времени цепи выпрямленного тока ротора для случая, соответствующего открытому состоянию тиристора VS1 Тm = Lэ/Rэ и учтя выше приведённые допущения, можно записатьКА1⋅ (Uзс – Кс⋅ ω)⋅ СМ = КТ⋅ (Тμ⋅р+1) ⋅ М.