Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Билет № 26
Содержание
- 1. Билет № 26
- 2. Правильные многоугольникиМногоугольник называется правильным, если все его
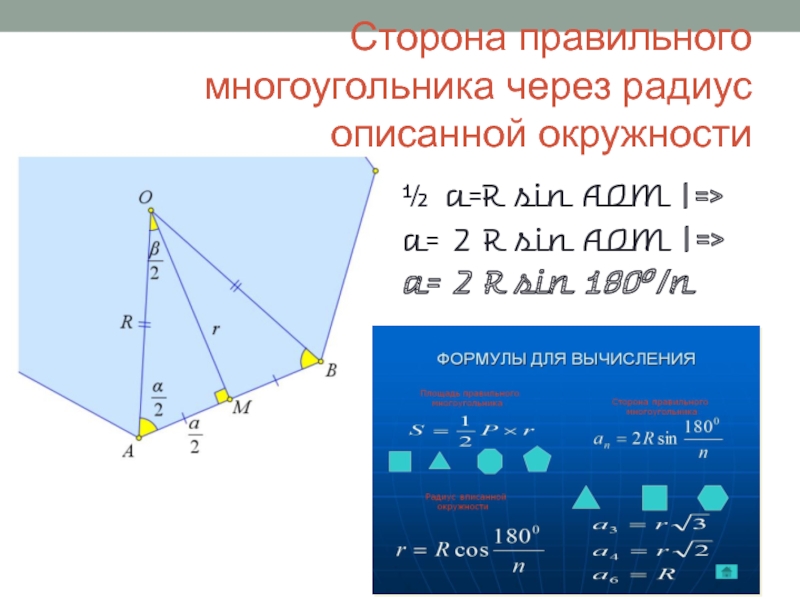
- 3. Сторона правильного многоугольника через радиус описанной окружности½
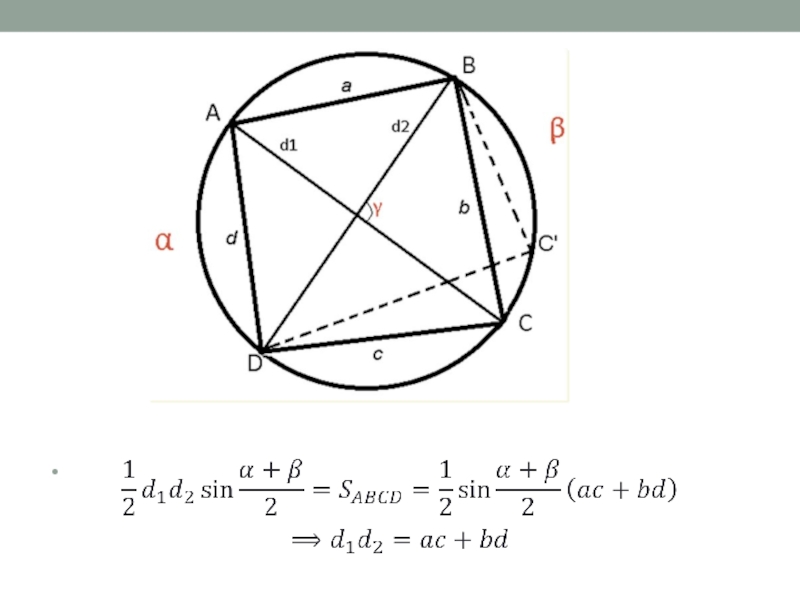
- 4. Теорема ПтолемеяПроизведение диагоналей вписанного в окружность четырехугольника равно сумме произведений противоположных сторонd1*d2 = a*c + b*d
- 5. Доказательство
- 6. Слайд 6
- 7. Скачать презентанцию
Правильные многоугольникиМногоугольник называется правильным, если все его стороны равны и все его углы равны.Пусть α – это угол правильного n-угольника, тогдаαn=(180°(n-2))/nА сумма вcех углов равнаSn=180°(n-2)
Слайды и текст этой презентации
Слайд 1Билет № 26
Правильные многоугольники. Сторона правильного многоугольника через радиус вписанной
и описанной окружности.
Слайд 2Правильные многоугольники
Многоугольник называется правильным, если все его стороны равны и
все его углы равны.
Пусть α – это угол правильного n-угольника,
тогдаαn=(180°(n-2))/n
А сумма вcех углов равна
Sn=180°(n-2)