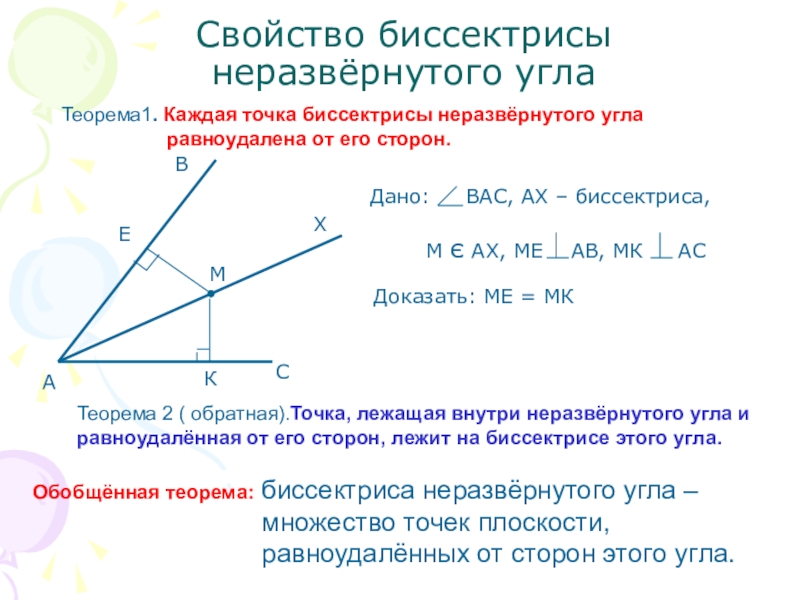
равноудалена от
его сторон.Доказать: МЕ = МК
Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.
Обобщённая теорема: биссектриса неразвёрнутого угла –
множество точек плоскости,
равноудалённых от сторон этого угла.