Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численный анализ истории погружения, термической эволюции и процессов генерации углеводородов в осадочных бассейнах
Содержание
- 1. Численный анализ истории погружения, термической эволюции и процессов генерации углеводородов в осадочных бассейнах
- 2. Осадочный нефтегазоносный бассейн подобен химическому реактору, генерирующему
- 3. Первый шаг моделирова-ния: данные из всех источ-ников,
- 4. Основные задачи, решаемые системой моделирования ГАЛО:
- 5. Слайд 5
- 6. Следующие данные привязаны к конкретным скважинам:-
- 7.
- 8. Слайд 8
- 9. Сравнение вычисленных значений пористости пород, температур и
- 10. Уплотнение осадков, история погружения бассейна и пористость
- 11. В системах моделирования бассейнов имеют дело с
- 12. Δz1·(1-ϕ(z1)) = Δz2·(1-ϕ(z2)) где ϕ(z)- пористость на
- 13. Изменение пористости с глубиной Пористость - важнейшая характеристика
- 14. В случае так называемого нормального давления поровое
- 15. Ситуация, когда пористость пород в разрезе является
- 16. При моделировании бассейнов задают свой закон изменения
- 17. Для песчаника – линейная зависимость или ϕ(z)
- 18. В процедуре численного моделировании бассейнов процесс формирования
- 19. В зависимости от начальной пористости осадков значение
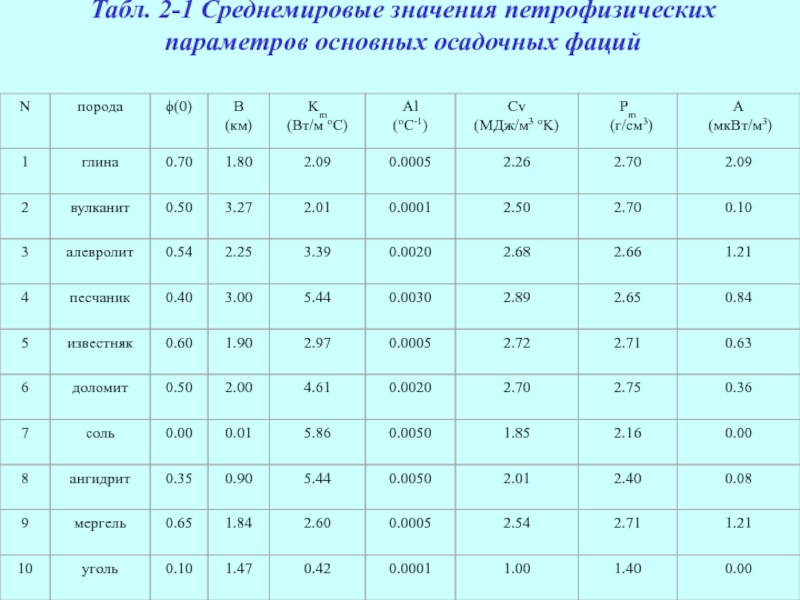
- 20. Табл. 2-1 Среднемировые значения петрофизических параметров основных осадочных фаций
- 21. Для смеси пород пористость вычисляется по следующему
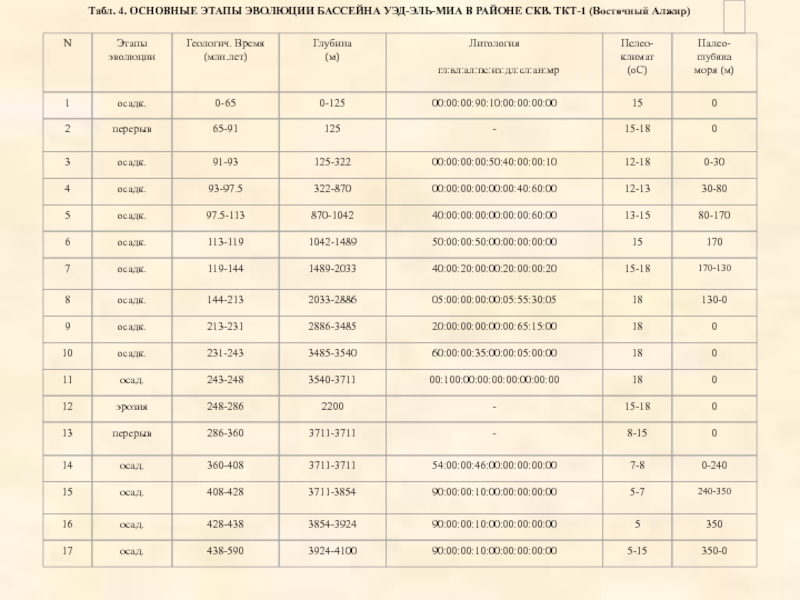
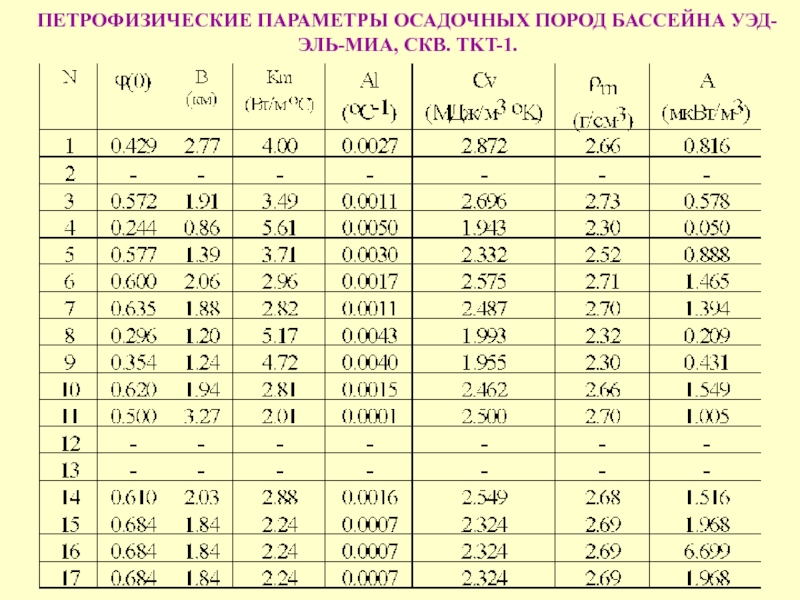
- 22. ПЕТРОФИЗИЧЕСКИЕ ПАРАМЕТРЫ ОСАДОЧНЫХ ПОРОД БАССЕЙНА УЭД-ЭЛЬ-МИА, СКВ. TKT-1.
- 23. Распределение пористости с глубиной (рассчитанные и измеренные
- 24. Пористость пород может иметь различные значения в
- 25. Физическая или полная пористость ϕtotal, это объём,
- 26. Пористость течения жидкости в породах ϕflow --
- 27. Пористость течения и диффузии жидкости ϕdiff -связывает
- 28. Оценка пористости пород по данным скважинного каротажа.
- 29. Оценка пористости пород по данным скважинного каротажа.
- 30. Оценка пористости пород по данным скважинного каротажа.
- 31. Пористость-проницаемостьПроницаемость определяет скорость течения жидкости в пористых
- 32. Проницаемость - наиболее резко меняющийся (по x,
- 33. Ряд полуэмпирических соотношений используются для связи проницаемость
- 34. Согласно (*), проницаемость глин k=(6.25; 0.62; и
- 35. Проницаемость пород для течений вдоль простирания слоя
- 36. Генерация АВПД Аномальное поровое давлениеР > Pg=ρw⋅g⋅z
- 37. Аномальные давления, созданные в одном месте, могут
- 38. Согласно уравнению диффузии для давления:где βb =
- 39. Для резервуара толщиной Hc, окружённого сверху и
- 40. Для описания изменения давления поровой жидкости со
- 41. k – проницаемость и μ -
- 42. Неравновесное уплотнение При медленном погружении осадки будут
- 43. Предел прочности на растяжения составляет обычно 70
- 44. Согласно оценкам, максимально допустимая проницаемость пород, способная
- 45. Зоны АВПД при неравновесном уплотнении могут развиваться
- 46. Тектоническое сжатие Латеральное тектоническое сжатие может
- 47. Акватермальное расширение поровой жидкости Рост АПД за
- 48. Повышение порового давления за счет процессов диагенеза
- 49. Генерация углеводородов как причина АВПД Преобразование
- 50. С приближением к порогу миграции поровое давление
- 51. Вторичный крекинг жидких УВ – источник АВПД Ряд
- 52. Течение грунтовых вод и другие источники
- 53. Выводы Возникновение зон АВПД относится к локальным событиям
- 54. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Численный анализ истории погружения, термической эволюции и процессов генерации углеводородов
в осадочных бассейнах
(« Моделирование Бассейнов »)
Слайд 2
Осадочный нефтегазоносный бассейн подобен химическому реактору, генерирующему УВ. Но, в
отличие от реактора, где исходный состав продуктов, продолжительность реакций, температура
и давление контролируются техническими средствами, в осадочных бассейнах мы можем лишь с некоторой точностью реконструировать условия формирования залежей УВ. И лучшим средством для этого служат компьютерные системы моделирования бассейнов.Анализ эволюции осадочного нефтегазоносного бассейна требует понимания большого числа процессов, действовавших в пределах этого геологического объекта за всё время его существования:
Погружения, поднятия и деформации бассейна
Палеогеографических и палеоклиматических условий развития бассейна
Условий осадконакопления и типа отложений
Кондуктивного и конвективного теплопереноса в бассейне
Кинетики преобразования ОВ и генерации УВ породами бассейна
Переноса жидкости, с особой ролью первичной и вторичной миграции нефти и газа
Формирования ловушек и анализа их надёжности
Процессов аккумуляции, преобразования и потери УВ.
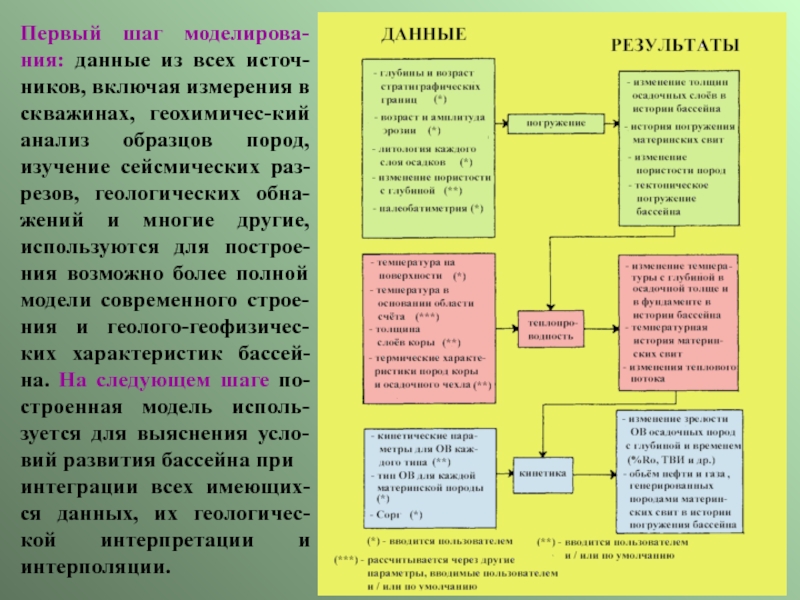
Слайд 3Первый шаг моделирова-ния: данные из всех источ-ников, включая измерения в
скважинах, геохимичес-кий анализ образцов пород, изучение сейсмических раз-резов, геологических обна-жений
и многие другие, используются для построе-ния возможно более полной модели современного строе-ния и геолого-геофизичес-ких характеристик бассей-на. На следующем шаге по-строенная модель исполь-зуется для выяснения усло-вий развития бассейна приинтеграции всех имеющих-ся данных, их геологичес-кой интерпретации и интерполяции.
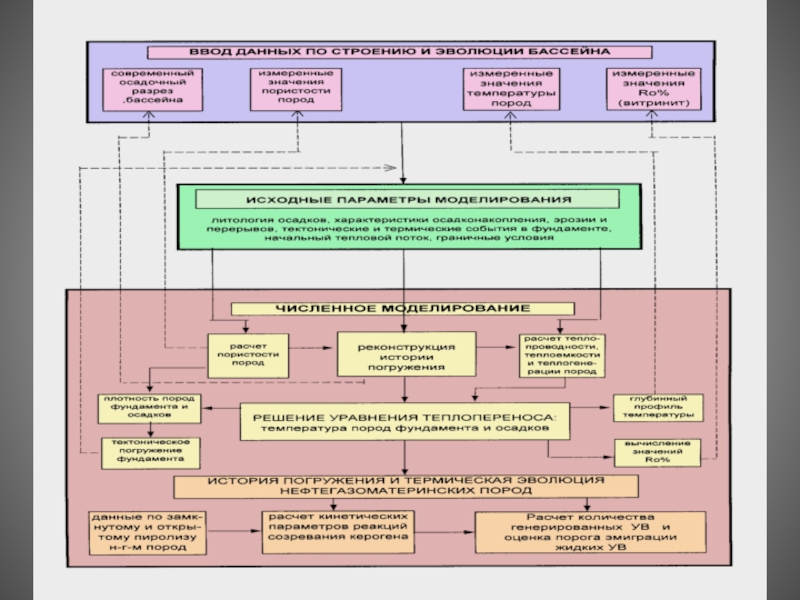
Слайд 4Основные задачи, решаемые системой моделирования ГАЛО:
1. Численное
восстановление истории погружения бассейна.
2. Расчёт изменения термического режима
осадочной толщи и подсти-лающей литосферы бассейна в условиях термической и тектоничес-
кой активизации района, внедрения интрузий и резких колебаний
климата.
3. Численная оценка изменения степени метаморфизма органического
вещества осадочной толщи бассейна
4. Реконструкция истории реализации нефтегазогенерационного потен-
циала бассейна и оценка порога первичной эмиграции жидких УВ.
5. Восстановление спектра химико-кинетических реакций, управляю-
щих процессами созревания ОВ материнских свит бассейна.
Слайд 6Следующие данные привязаны к конкретным скважинам:
- Толщины и возраст
слоев осадков
- Распределение пористости в уплотненных породах
- Давление в
породах- Температуры пород
- Распределение зрелости органического вещества осадков
- измерения глубинных температур
- оценки палеотемператур (включения жидкостей и другие методы)
Геохимические характеристики генерационных
своств пород (экстракция и данные пиролиза образцов материнских пород)
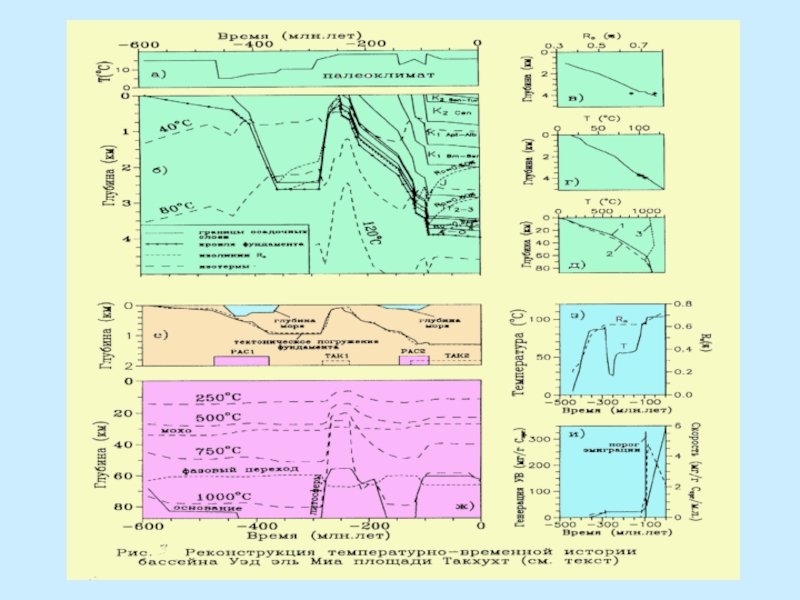
Слайд 9Сравнение вычисленных значений пористости пород, температур и отражательной способности витринита
с измеренными, а также анализ относительных вариаций амплитуд тектонического погружения
фундамента, составляют основу контроля справедливости рассчитанной модели эволюции бассейна.В пакетах MATOIL, GENEX, TEMISPACK, PDI в основании осадочной толщи или близко от неё задаётся тепловой поток как кусочно-линейная функция времени. Её форма определялась из условия совпадения вычисленных и наблюденных значений отражательной способности витринита (Doligez et al.,1986; Nakayama and Lerche, 1987; Welte and Yalcin, 1988; Ungerer, 1990 и др).
В системе ГАЛО область поиска распределения температуры кроме осадочной толщи включала ещё и подстилающую литосферу с частью астеносферы (если та существовала на глубинах менее 200 км). Это обеспечивало интеграцию процессов, определяющих термический режим осадочной толщи бассейна, с термической и тектонической историей подстилающей литосферы и позволяло использовать анализ кривой тектонического погружения бассейна для уточнения событий тепловой и тектонической истории его литосферы (слайд 8).
Слайд 10Уплотнение осадков, история погружения бассейна и пористость пород.
С погружением бассейна
осадочные породы сжимаются, уменьшая объём порового пространства и высвобождая часть
поровых вод .Слайд 11В системах моделирования бассейнов имеют дело с верти-кальными деформациями элемен-тов
сети (скелета) при уплотнении пород. При этом процесс консоли-дации осадков
рассматривается как медленное вертикальное ади-абатическое сжатие области, за-полненной осадочным материа-лом. Каждый из элементов осадоч-ного слоя уменьшается в размераx (сжимается) в соответствии с уменьшением пористости породы под действием вышележащей нагрузки.Δt - интервал времени отложения элементарного слоя осадков, Δz, на поверхности бассейна. Консолидация лежащих ниже осадков под нагрузкой слоя Δz предполагается мгновенной. В периоды эрозии и перерывов в осадконакоплении мощности слоёв осадков остаются неизменными.
Слайд 12Δz1·(1-ϕ(z1)) = Δz2·(1-ϕ(z2))
где ϕ(z)- пористость на глубине z и
Δz1 и Δz2 - толщины слоя на глубинах z1 and
z2.На этом соотношении основана процедура “разуплотнения” (decompaction), применяемая во всех системах моделирования бассейнов для восстановления истории погружения осадочных бассейнов.
В моделировании бассейнов процесс консолидации осадков рассматривается в обычном предположении о том, что изменение объёма твердой матрицы пород под действием лежащей выше нагрузки пренебрежимо по сравнению с уменьшением объёма их порового пространства (Perrier and Qublier, 1974):
Слайд 13Изменение пористости с глубиной
Пористость - важнейшая характеристика осадочных пород, определяющая
их тепловые и механические свойства.
Пористость - функция эффективного напряжения
в скелете пород, σ, передающегося от кристалла к кристаллу на контактах зёрен: ϕ = ϕ (σ), где σ = Sg – P
Р - поровое давление, Pmin = ρw⋅g⋅z – гидростатическое давление. Sg - полная нагрузка от давления осадков:
ρb - средняя плотность пород в столбце осадков высотой z.
Следовательно, вес слоя осадков, Sg, поддерживается совместным действием эффективных напряжений скелета, σ, и давлением жидкости в порах, P
Sg = σ + P
Слайд 14В случае так называемого нормального давления поровое давление равно гидростатическому:
P = ρw⋅g⋅z
и тогда:
σ = (ρb - ρw)⋅g⋅zа величина эффективных напряжений в скелете определяется глубиной погружения и разностью между средней плотностью насыщенных водой осадков и плотностью воды.
ПРОБЛЕМЫ:
В глубоких частях бассейна (z > 2 – 3 км, Т >= 70 – 100°C кон-солидация осадков привлекает процессы растворения и осажде-ния минералов (кварца и др.), которые сильно зависят от темпе-ратуры и в значительно меньше от эффективных напряжений σ (Boorlykke, 1999). Консолидация осадков, вызванная хими-ческим диагенезом, т.е. немеханическая, может вызвать более интенсивное сокращение пористости, чем обычная механическая консолидация. Химические процессы более эффективно умень-шают проницаемось пород за счёт цементации материала, чем обычное уплотнение (Nygard et al., 2004).
Слайд 15 Ситуация, когда пористость пород в разрезе является однозначной функцией давления
или глубины, является признаком нормального распределения порового давления в бассейне
с глубиной, т.е. когда оно соответствует гидростатическому градиенту на данной глубине. Зоны АВПД развиваются в сравнительно ограниченных областях осадочного разреза, их возникновение является локальным событием по месту и времени своего проявления. Развитие ряда бассейнов протекало в отсутствии заметных аномальных поровых давлений в породах бассейна.Поэтому использование заранее известной зависимости пористости от давления или глубины является общепринятым в системах моделирования бассейнов. Влияние локальных зон АВПД, анализируется обычно в рамках приближённых решений с подбором масштаба уплотнения породы.
Слайд 16При моделировании бассейнов задают свой закон изменения пористости породы с
глубиной для каждого из осадочных слоёв бассейна. При этом рассматривают
три возможности:1) экспоненциальная зависимость пористости от глубины: ϕ = ϕ(0) exp(-z / B)
2) линейная (некоторые песчаники):
ϕ(z) = 0. для z > B и
ϕ(z) = ϕ(0)⋅( 1 - z / B ) для 0 ≤ z ≤ B
3) и произвольная заданная функция ϕ = ϕ(z).
Выше ϕ(0) - пористость осадков при отложении на поверхности (среднее для верхних 100-150 м осадков данной литологии) и B - масштаб изменения пористости с глубиной.
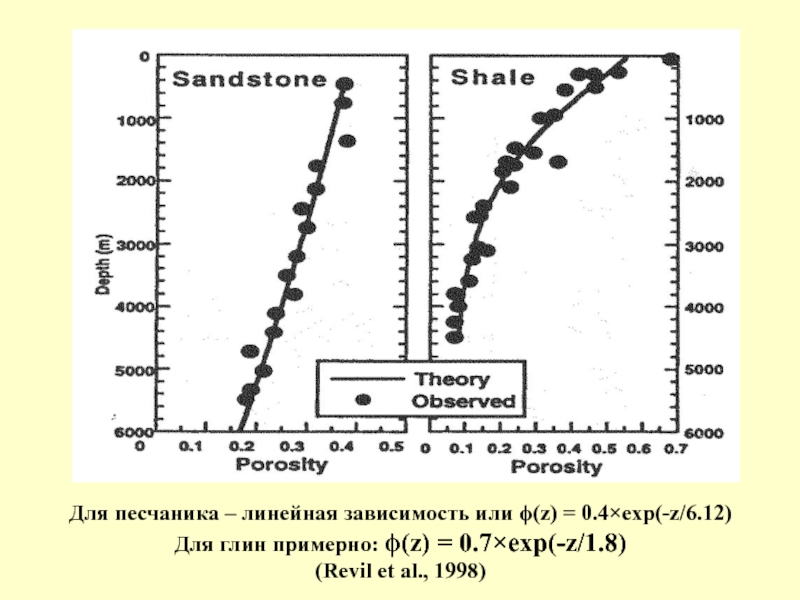
Слайд 17Для песчаника – линейная зависимость или ϕ(z) = 0.4×exp(-z/6.12)
Для глин
примерно: ϕ(z) = 0.7×exp(-z/1.8)
(Revil et al., 1998)
Слайд 18В процедуре численного моделировании бассейнов процесс формирования осадочной толщи воспроизводиться
последовательным отложением тонких слоёв неуплотнённых осадков Δz1 на поверхности бассейна
(слайд 11). Поэтому оценки необходимого объёма неуплотнённых осадков являются составной частью моделирования. При отложении элементарного слоя на поверхности, породы, лежащие ниже, уплотняются. Применяя соотношение (1) к мощности данного слоя z1 ≤ z ≤ z2, наблюдаемой в современном разрезе, получаем объём неуплотнённыx литологически однородных осадков Н0, который необходимо отложить дискретными порциями Δz1 на поверхности бассейна, чтобы в итоге с учётом уплотнения получить наблюдаемую в современном разрезе толщу:
Для экспоненциального закона (1) отсюда получаем:
Слайд 19В зависимости от начальной пористости осадков значение Ho может в
2-3 раза превосходить мощность слоя в современном разрезе. Процесс уменьшения
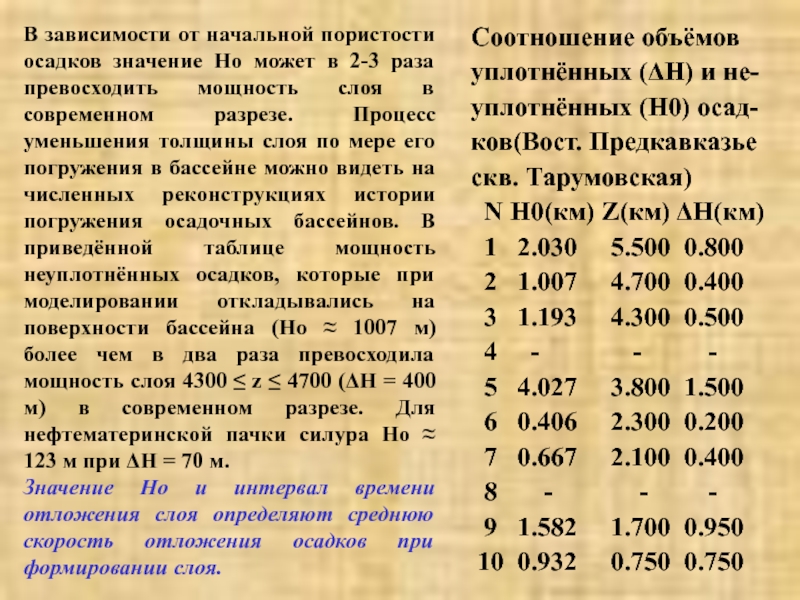
толщины слоя по мере его погружения в бассейне можно видеть на численных реконструкциях истории погружения осадочных бассейнов. В приведённой таблице мощность неуплотнённых осадков, которые при моделировании откладывались на поверхности бассейна (Ho ≈ 1007 м) более чем в два раза превосходила мощность слоя 4300 ≤ z ≤ 4700 (ΔH = 400 м) в современном разрезе. Для нефтематеринской пачки силура Ho ≈ 123 м при ΔH = 70 м.Значение Ho и интервал времени отложения слоя определяют среднюю скорость отложения осадков при формировании слоя.
Соотношение объёмов уплотнённых (ΔH) и не- уплотнённых (H0) осад-ков(Вост. Предкавказье
скв. Тарумовская)
N H0(км) Z(км) ΔH(км)
1 2.030 5.500 0.800
2 1.007 4.700 0.400
3 1.193 4.300 0.500
4 - - -
5 4.027 3.800 1.500
6 0.406 2.300 0.200
7 0.667 2.100 0.400
8 - - -
9 1.582 1.700 0.950
10 0.932 0.750 0.750
Слайд 21Для смеси пород пористость вычисляется по следующему соотношению (осреднение по
обратным объёмам скелета пород; Doligez et al., 1986) :
Ci
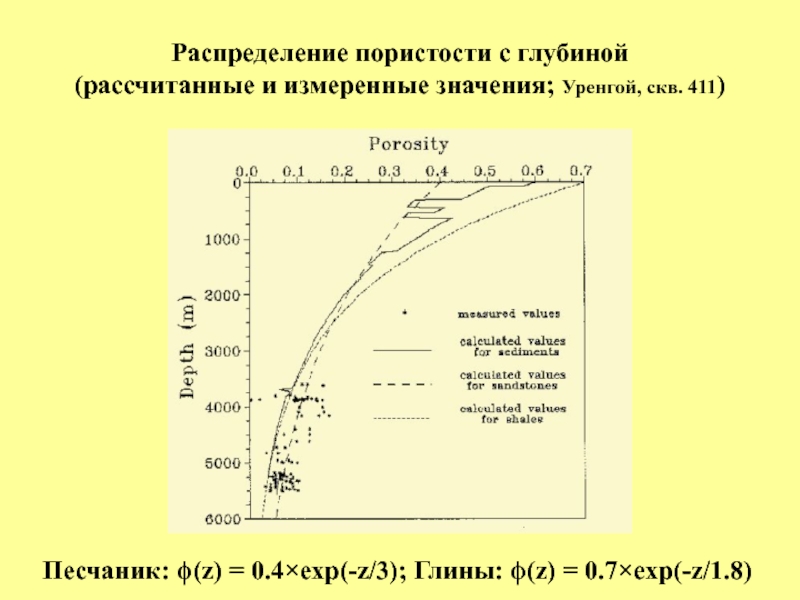
- доля i-ой литологической единицы в породе, n – число литологических единиц и ϕi(Z) - пористость пород i-ой литологической единицы на глубине Z. Примеры таких определений для пород бассейна Уэд эль Миа приведны ниже. Слайд 23Распределение пористости с глубиной
(рассчитанные и измеренные значения; Уренгой, скв. 411)
Песчаник:
ϕ(z) = 0.4×exp(-z/3); Глины: ϕ(z) = 0.7×exp(-z/1.8)
Слайд 24Пористость пород может иметь различные значения в зависимости от метода
её измерения и от процесса, для описания которого она применяется
Различают
следующие основные типы пористости:Физическая или полная пористость ϕtotal
«Внутрисвязанная» пористость ϕwater
Пористость течения жидкости в породах ϕflow
Пористость диффузии жидкости ϕdiff
Геохимическая пористость ϕgeochem
Слайд 25Физическая или полная пористость ϕtotal,
это объём, не занятый кристаллической
матрицей. Он определяется отношением объёма пустот (в том числе и
изолированных) к полному объёму породы и вычисляется из сравнения плотности скелета пород с плотностью породы. Она особенно важна для моделирования, так как участвует в расчётах уплотнения пород и в определении термофизических параметров пород (теплопроводности, теплоёмкости и теплогенерации).«Внутрисвязанная» пористость ϕwater
- определяется выделением воды из объёма породы и измерением её количества. Она всегда будет меньше полной (физической) ϕtotal, так как всегда остаются включения воды в мелких порах, которые не удаётся удалить высушиванием.
(При ртутных же измерениях пористости давление, требуемое для внедрения ртути в мелкие поры, может разрушить исходную структуру глин; Pearson, 1999).
Слайд 26Пористость течения жидкости в породах ϕflow -
- определяет скорость потока
жидкости Vflow=VDarcy/ϕrock через скорость Дарси VDarcy=-(k/μ)⋅(dP/dx), k – проницаемость, μ
- динамическая вязкость жидкости, dP/dx – градиент давления. (Скорость Дарси - объём жидкости, проходящий в единицу времени через единицу площади (породы), перпендикулярной потоку, вызванному градиентом давления dP/dx.)Пористость течения меньше «внутрисвязной» пористости, так как поры, открытые лишь с одного края не вносят вклада в пористость течения, но включаются во «внутрисвязную» пористость.
В аргиллитах пористость течения ϕflow будет принципиально связана с микротрещинами.
Слайд 27Пористость течения и диффузии жидкости ϕdiff -
связывает диффузию в породе
с диффузией в чистой воде. В глинистых породах диффузионная пористость
для воды эквивалентна пористости потока, но для диффузии раствора она меньше последней.Геохимическая пористость ϕgeochem
необходима, чтобы моделировать состав поровых вод и перенос реактивов в плохо проницаемых материалах, типа плотных глин. Эта пористость, по сути, является объёмом жидкости, в котором имеют место реакции. В глинистых породах она мало отличается от диффузионной пористости. Геохимическая пористость в аргиллитах может составлять 0.3 – 0.7 от значения ϕwater или ϕtotal. Такие неопределённости не играют большой роли в решении уравнений переноса, но важны при моделировании состава поровых вод.
Cоответствующие пористости удовлетворяют неравенству глин (Pearson, 1999):
ϕflow ≤ ϕdiff ≈ ϕgeochem ≤ ϕwater ≤ ϕtotal
Слайд 28Оценка пористости пород по данным скважинного каротажа.
Звуковой каротаж
Звуковой каротаж
- запись времени, необходимого для прохождения волн сжатия, излучаемых прибором,
через 1 фут (30.48 см) формации до приёмника. При известной литологии пористость может быть определена из соотношения Δt = Δtma ⋅(1 - ϕ) + ϕ⋅(Δtf) где Δtma есть время прохода звука через твёрдую матрицу пород (51.3 – 55.5 μсек (10-6 сек)/фут для песчаников и 43.5 – 47.6 μсек/фут для известняков). (Время прохождения сигнала через поровую жидкость (Δtf) зависит от солёности вод и составляет 189 μсек/фут для пресной воды.).Слайд 29Оценка пористости пород по данным скважинного каротажа.
гамма-каротаж (плотностной каротаж)
гамма-каротаж
(плотностной каротаж) – здесь используется Комптон-эффект: гамма лучи из источника
рассеиваются на электронах в породе формации, давая информацию о плотности электронного облака и вместе с ней о плотности породы и из соотношения:= ρma ⋅(1 - ϕ) + ϕ⋅(ρf) ,
где ρma – плотность твёрдой матрицы пород и ρf – плотность поровой жидкости, ϕ - пористость.
(для эвапоритовых пород (соль, сильвит (KCl)) и угля метод неточен. Присутствие остаточного газа в порах также может исказить результаты анализа.)
Слайд 30Оценка пористости пород по данным скважинного каротажа.
Нейтронный γ каротаж
Нейтронный
γ-каротаж – измерение интенсивности γ-излучения, вызванного облучением пород нейтронами. Интенсивность
γ-излучения зависит от степени замедления и захвата нейтронов атомами среды. Основной замедлитель быстрых нейтронов – водород и неплохой – хлор. Поэтому нейтронный γ-каротаж позволяет выделить породы, содер-жащие водород и хлор, в том числе нефтеносные и водонос-ные слои, и дать меру содержания воды в породе и тем, са-мым, пористости породы. (Большие ошибки - от присутствия глинистых минералов, содержащих связанную воду).Из всех видов каротажа звуковой используется наиболее часто.
Слайд 31Пористость-проницаемость
Проницаемость определяет скорость течения жидкости в пористых средах, вызванного градиентом
давления dP/dxi в направлении оси Xi
k – проницаемость, μ
- динамическая вязкость жидкости (для воды μw ≈ 1.14×10-3 Па⋅сек) и P давление (Па). Для k=10-17 м2 и dP/dx=(100 м ⋅ρ⋅g / 1000 м) ≈ 103 н/м3=103 Па/м объём грунтовых вод (м3), переносимый в сек через 1 м2 породы (или скорость Дарси), равен VDarsy= 8.8×10-12 м3/м2сек. В таком течении скорость жидкости равна V=VDarsy/ϕ, и составляет около 4.4×10-11 м/сек ≈ 1.39×10-3 м/год. Распределение прони-цаемости по глубине и площади бассейна оп-ределяет во многом рас-положение зон аномаль-но высоких поровых давлений (АВПД).
Непроницаемые и отчасти практически непроницае-мые породы характеризу-ются проявлением гидро-литического растрескива-ния в ответ на генерацию в порах АВПД.
Слайд 32Проницаемость - наиболее резко меняющийся (по x, z и t)
и наиболее трудно определимый параметр осадочных пород.
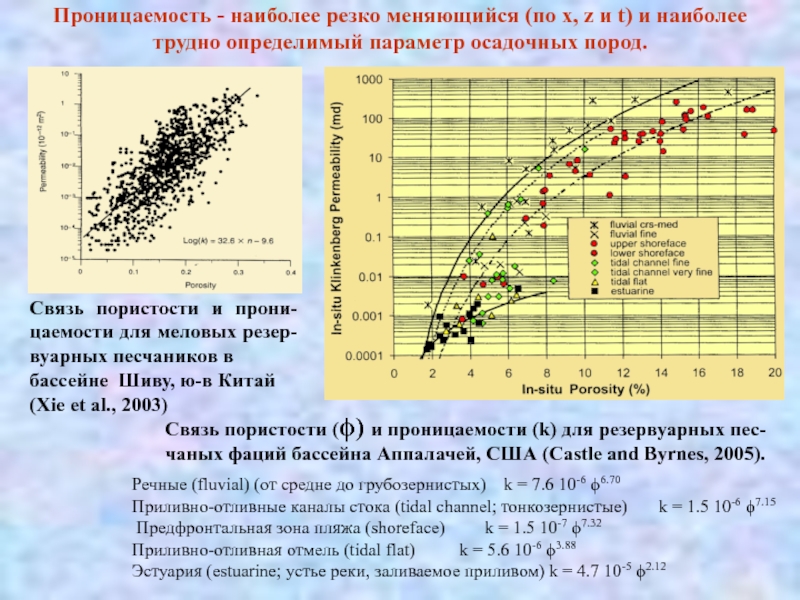
Связь пористости и
прони-цаемости для меловых резер-вуарных песчаников в бассейне Шиву, ю-в Китай
(Xie et al., 2003)
Связь пористости (ϕ) и проницаемости (k) для резервуарных пес-
чаных фаций бассейна Аппалачей, США (Castle and Byrnes, 2005).
Речные (fluvial) (от средне до грубозернистых) k = 7.6 10-6 ϕ6.70
Приливно-отливные каналы стока (tidal channel; тонкозернистые) k = 1.5 10-6 ϕ7.15
Предфронтальная зона пляжа (shoreface) k = 1.5 10-7 ϕ7.32
Приливно-отливная отмель (tidal flat) k = 5.6 10-6 ϕ3.88
Эстуария (estuarine; устье реки, заливаемое приливом) k = 4.7 10-5 ϕ2.12
Слайд 33Ряд полуэмпирических соотношений используются для связи проницаемость осадочных пород с
пористостью
Модельные соотно-шения «пористость -проницаемость», используемые раз-ными авторами: (Olsen, 1962;
Mann and MacKenzie, 1990; Maubeuge and Lerche, 1994; Luo and Vasseur, 1996 Dewhurst et al., 1999).Формула Казени-Кармана
k=0.2 ϕ3 / [(1-ϕ)2 S02] для ϕ ≥ 10%
k=2.0 ϕ5 / [(1-ϕ)2 S02] для ϕ < 10% (*)
S0 - специфическая поверхность ((1-3) 108 м2/м3 для уп-лотнённых глин; Ungerer et al.,1990). Неплохо для песча-ных фракций при корректном задании S0 , но заметно за- нижает проницаемость в глинах.
Сравнение значе-ний «пористость-проницаемость», измеренных для образцов двух ти-пов аргиллитов, с вычисленными по формуле Козени-Кармана (Dewhurst et al., 1999).
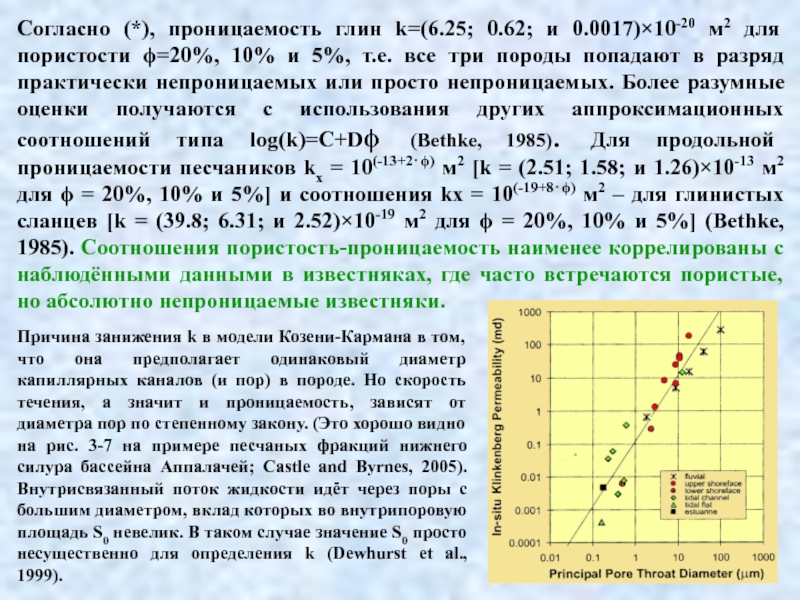
Слайд 34Согласно (*), проницаемость глин k=(6.25; 0.62; и 0.0017)×10-20 м2 для
пористости ϕ=20%, 10% и 5%, т.е. все три породы попадают
в разряд практически непроницаемых или просто непроницаемых. Более разумные оценки получаются с использования других аппроксимационных соотношений типа log(k)=C+Dϕ (Bethke, 1985). Для продольной проницаемости песчаников kx = 10(-13+2⋅ϕ) м2 [k = (2.51; 1.58; и 1.26)×10-13 м2 для ϕ = 20%, 10% и 5%] и соотношения kx = 10(-19+8⋅ϕ) м2 – для глинистых сланцев [k = (39.8; 6.31; и 2.52)×10-19 м2 для ϕ = 20%, 10% и 5%] (Bethke, 1985). Соотношения пористость-проницаемость наименее коррелированы с наблюдёнными данными в известняках, где часто встречаются пористые, но абсолютно непроницаемые известняки.Причина занижения k в модели Козени-Кармана в том, что она предполагает одинаковый диаметр капиллярных каналов (и пор) в породе. Но скорость течения, а значит и проницаемость, зависят от диаметра пор по степенному закону. (Это хорошо видно на рис. 3-7 на примере песчаных фракций нижнего силура бассейна Аппалачей; Castle and Byrnes, 2005). Внутрисвязанный поток жидкости идёт через поры с большим диаметром, вклад которых во внутрипоровую площадь S0 невелик. В таком случае значение S0 просто несущественно для определения k (Dewhurst et al., 1999).
Слайд 35Проницаемость пород для течений вдоль простирания слоя (kx) , как
правило, заметно больше, чем проницаемость для потоков вкрест его простирания
(kz). Так, для песчаных пород kx/kz = 2.5, а для глинистых сланцев kx / kz = 10 и более (Bethke, 1985; 1989; England et al.,1987). Проницаемости горизонтально-слоистых средνz-гидролитическая проводимость (ν=k⋅ρ⋅g/μ) в вертикальном направлении, νx - в горизонтальном, то для структуры мощностью d, составленной из последовательности n горизонтальных слоев с мощностями di и проводимостями νzi, νxi эффективные проводимости слоя будут равны νz = d / ∑i=1n (di/νzi) для вертикального (поперёк слоёв) течения и νx = [∑i=1n (di⋅νxi)]/d – для горизонтального (вдоль напластования) потока жидкости (Freeze and Cherry, 1979).
Отношение латерального и вертикального потоков жидкости в объёме пород определяется отношением проводимостей пород наиболее проницаемого латерального канала к проводимости наименее проницаемых пород (обычно) стенок канала.
При вторичной миграции вертикальный массоперенос становится пренебрежимым по сравнению с латеральным при kx > 0.001 Дарси.
Горизонтальная и вертикальная проницаемости
Слайд 36Генерация АВПД
Аномальное поровое давление
Р > Pg=ρw⋅g⋅z
где Pg –
гидроста-
тическое давление.
Механизмы формирования
АВПД:
Неравновесное уплотнениe
Тектоническое сжатие
Акватермальное расширение ж-ти
Диагенез
породГенерация УВ
Течение грунтовых вод и другие
Модельные (точечные линии) и наблюдаемые (сплошные линии) значения порового давления (справа) и пористости (слева) в осадочном разрезе грабена Викинг, Северное море (Bolas et al., 2004)/
Распределение пористости и давления с глубиной
Слайд 37Аномальные давления, созданные в одном месте, могут перераспределяться в соседние
и более отдаленные участки бассейна.
Рост АВПД за счет изменений
объёма пор и/или поровой жидкости будет эффективным лишь при хорошем качестве изоляции жидкости в порах или в ловушке. Поэтому пересмотр роли некоторых механизмов генерации АВПД в последние 10-15 лет в основном был связан с изменением в оценках водоизолирующих свойств пород.
Слайд 38Согласно уравнению диффузии для давления:
где βb = -(1/V)⋅(∂V/∂Pe)T – изотермическая
сжимаемость осадков, ϕ - пористость, Р – поровое давление, z
– глубина, t – время, Т – температура, Pe = Pt – P – эффективное напряжение на границах зёрен, k – проницаемость и μ - динамическая вязкость поровой жидкости. Из этого уравнения следует грубая оценка масштаба времени диссипации давления (Muggeridge et al.,2005):T ~ (H2⋅βb⋅μ⋅ϕ) / k
где Н – толщина удерживающего барьера (в м), βb – изотермическая сжимаемость осадков (в Ра-1), μ - динамическая вязкость (в Н⋅сек/м2), k – проницаемость
(в м2).
Слайд 39Для резервуара толщиной Hc, окружённого сверху и снизу двумя слоями
с породами барьера толщиной Hb каждый, то масштаб времени релаксации
давления можно оценить по формуле (Muggeridge et al.,2005):где индекс с относится к породам резервуара, а индекс b – к породам барьера.
Например, для Hb = 100 м, Нс = 50 м, μ = 8×10-4 н⋅сек/м2, βc ~ βb ~ = 6×10-10 Pa-1, kb = 10-18 – 10-24 м2
Получаем: Т = 7.6×(1 – 106) лет
Слайд 40Для описания изменения давления поровой жидкости со временем и в
пространстве используется уравнение неразрывности для вертикального движения поровой жидкости в
сжимаемой матрице (Mudford, 1988; 1990):Здесь: ϕ - пористость, βf = -(1/Vf)⋅(∂Vf/∂P)T = 1.4×10-14 Pa-1 – изотермическая сжимаемость поровых жидкостей, βb = -(1/V)⋅(∂V/∂Pe)T = 5×10-10 Pa-1 – изотермическая сжимаемость осадков, βS = -(1/VS)⋅(∂VS/∂Pe)T (βS << βb , βf ) – изотермическая сжимаемость cкелета пород, αf = -(1/Vf)⋅(∂Vf/∂Т)Р = 7×10-4 К-1 – изобарический коэффициент термического расширения поровых жидкостей, αb = -(1/V)⋅(∂V/∂Т)Pe – изобарический коэффициент термического расширения осадков, αS = -(1/VS)⋅(∂VS/∂Т)Pe изобарический коэффициент термического расширения cкелета пород,
Слайд 41 k – проницаемость и μ - динамическая вязкость поровой
жидкости, Р – поровое давление, Pt – полное давление (литостатическое),
Pe = Pt – P – эффективное напряжение на границах зёрен, z – глубина, t – время, Т – температура, Qf – скорость генерации жидкости (2.5×10-13кг/(м3сек)), g – ускорение силы тяжести (9.81 м/сек2), ρf – плотность поровой жидкости (1030 кг/м3), ρS – плотность скелета пород (1030 кг/м3). Уравнение (10) справедливо только для однофазной жидкости.1-ый член справа–изменение давления при течении жидкости (поток Дарси), 2-ой – изменение давления за счёт изменения давления нагрузки, 3-ий – акватермальное давление, за счёт изменения температуры, изменение Р за счёт вариаций пористости и последний – представляет источники жидкости.
Слайд 42Неравновесное уплотнение
При медленном погружении осадки будут нормально уплотнены, т.е.
будет равновесие между нагрузкой и сокращением объёма пор. Давление поровой
жидкости р остаётся гидростатическим: Р = 0 ∫ ZH ρw⋅g⋅dz.Быстрое погружение требует быстрого оттока воды из пор. Тогда, если жидкость не может покидать область консолидации достаточно быстро, (например, низкая проницаемости вмещающих пород), давление поровой жидкости начинает превышать гидростатическое. Такой процесс известен как неравновесное уплотнение (бассейны Галф Коаст, Каспийское и Северное моря).
При этом поровое давление не превосходит литостатическое. Однако, оно может превышать прочность пород на растяжение, и тогда развивается гидролитическое растрескивание.
Слайд 43Предел прочности на растяжения составляет обычно 70 - 90% от
напряжения нагрузки, но может быть и выше на глубинах 5000
и более м.При Z < 1300-2000 м гидролитическое растрескива-ние при неравновесном уплотнении маловероятно даже при скоростях отложения осадков более 600 м/млн. лет, так как проницаемость осадков здесь ещё велика.
Численные оценки (Shi and Wang, 1986; Mudford, 1988, 1990; Mudford and Best, 1989; Forbes et al, 1992; Osborne and Swarbrick, 1997) показывают, что при скоростях осадконакопления меньших 100 м/млн. лет появление зон АВПД за счет механизма неравновесного уплотнения маловероятно для всего интервала глубин.
Слайд 44Согласно оценкам, максимально допустимая проницаемость пород, способная в течении более
миллиона лет поддерживать свойства ловушки, составляет 10-21 - 10-23 м2
(10-6 - 10-8 мд). Большинство измеренных проницаемостей глин превышают этот предел.Поэтому аномальное давление, создаваемое неравновесным уплотнением, относится, как правило, к нестационарным эффектам. Со временем оно диссипирует либо за счет медленного вертикального потока жидкости и газа, либо за счет латеральной миграции через водоносные горизонты, вмещенные в слои глинистых сланцев (Osborne and Swarbrick, 1997).
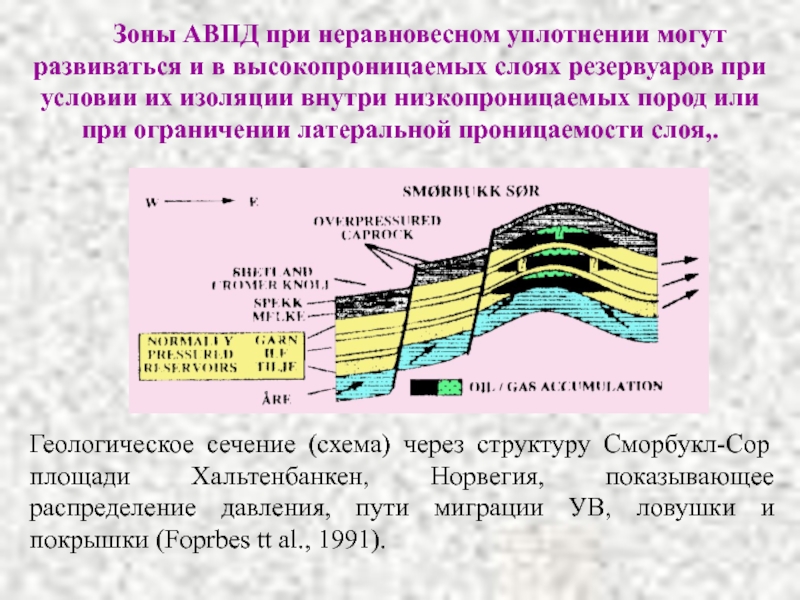
Слайд 45Зоны АВПД при неравновесном уплотнении могут развиваться и в высокопроницаемых
слоях резервуаров при условии их изоляции внутри низкопроницаемых пород или
при ограничении латеральной проницаемости слоя,.Геологическое сечение (схема) через структуру Сморбукл-Сор площади Хальтенбанкен, Норвегия, показывающее распределение давления, пути миграции УВ, ловушки и покрышки (Foprbes tt al., 1991).
Слайд 46 Тектоническое сжатие
Латеральное тектоническое сжатие может привести к росту
порового давления тем же путем, что и вертикальные напряжения, вызывающие
появление АВПД при неравновесном уплотнении. Однако, этот эффект будет более важен в современных тектонически активных областях. Известна, например, обширная зона с аномальным давлением, имеющая ширину 40-150 км и длину 650-800 км, связанная с трансформным разломом Сан Андреас в Калифорнии (Sleep and Blanpied, 1992), аномально сжатые осадки обнаружены и под аккреционными призмами вблизи конвергентных краев плит (Fisher and Zwart, 1996). Соляной диапиризм также может вызвать появление зон АВПД в отдельных районах в окрестности диапира (Burrus J. and F. Andebert,1990). Например, широкое развитие в настоящее время аномально высоких пластовых давлений (АВПД) в подсолевых отложениях осадочного чехла и в прибортовых внутренних частях Прикаспийской впадины на глубинах, превышающих 3700 м, вызвано активизацией здесь неотектонкчеокнх движений (Котровский, 1986).В целом, тектонические процессы могут привести к быстрому возникновению зон АВПД и к столь же быстрой их релаксации в зависимости от геологического строения области и от характера тектонической активности в районе.
Слайд 47Акватермальное расширение поровой жидкости
Рост АПД за счет механизмов с
изменением объёма пор будет эффективным лишь при хорошем качестве изоляции
жидкости (ловушки). Это в особой степени относится к акватермальному механизму генерации АПД, так как расширение объёма жидкости при этом оказывается сравнительно малым (на 1.65% при росте температуры от 54 до 93°С) и легко диссипирует путем истекания жидкости из обьема в том числе и в низкопроницаемых породах. Прямые расчеты показывают, что акватермальное повышение порового давления оказывается пренебрежимым по сравнению с эффектом неравновесного уплотнения даже в породах с проницаемостью 3⋅10-12 мд (1 Дарси=10-12 м2), тогда как измеренная проницаемость реальных глин варирует от 1 10-1 - 1 10-8 мд (Luo and Vasseur, 1992). Ряд процессов, типа выделения газа и образования в порах двух или более фаз, могут уменьшать проницаемость песчаных пород и глин почти на 90% и все-таки этого не достаточно, чтобы обеспечить качественные ловушки для акватермального механизма повышения порового давления (Osborne and Swarbrick, 1997). Согласно современным воззрениям, этот механизм может быть эффективным либо в идеально непроницаемых эвапоритовых толщах, либо в течение очень короткого времени при внедрении интрузий.Слайд 48Повышение порового давления за счет процессов диагенеза пород
Исследования показали,
что рост обьема жидкости, связанный с дегидратацией смектита будет слишком
мал и не сможет генерировать заметных АПД даже при идеальных ловушках для жидкости (Bradley, 1975; Shi and Wang, 1986; Osborne and Swarbrick, 1997). Более того, реакции дегидратации будут подавляться с ростом порового давления (Osborne and Swarbrick, 1997). Что же касается перехода смектита в иллит, то исследования показывают, что соответствующие реакции достаточно медленны и в условиях реальных бассейнов должны приводить к плавному, постепенному (а не обвальному) высвобождению воды (Osborne and Swarbrick, 1997).Реакции преобразования гипса в ангидрит имеют место при температурах от 40 до 60°С и приводят к потере 39% связанной воды. Этот процесс мог бы генерировать АВПД на глубинах порядка 1 км, но маловероятно его участие в создании аномальных зон на больших глубинах (Jowett et al.,1993).
Рост цементации приводит к уменьшению размеров пор, а растворение минералов - к их увеличению, но создание АВПД зависит от того, насколько замкнута система, в которой имеют место эти процессы. Пока отсутствуют геологические примеры с доказательствами существенного участия этих процессов в формировании зон АВПД.
Слайд 49 Генерация углеводородов как причина АВПД
Преобразование керогена в жидкие
УВ, газ, остаток и сопутствующие продукты сопровождается увеличением объёма результирующего
продукта и в изолированной системе приводит к возникновению АВПД. При оценке процесса необходимо учитывать, что степень расширения объёма заметно варирует с изменением типа керогена. Мейснер (Meissner, 1980) - увеличении обьема вплоть до 25%. при переходе керогена в жидкие УВ, Унжере (Ungerer et al, 1983) - сокращение обьема на 3-6% при генерации УВ из Toarcian черных сланцев с ОВ типа II (Парижский бассейн). Изменение объёма при преобразовании керогена сильно варирует в зависимости от состава генерированных газов и плотности остаточного керогена и кокса (Osborne and Swarbrick, 1997).В то же время доказательства роста порового давления при созревании ОВ следуют из самого факта первичной миграции УВ из слабопроницаемых материнских пород. Эта миграция предполагает высокие внутренние поровые давления в материнских породах, которые способствуют выделению нефти через микропоры или микротрещины. Давления, обусловленного лишь плавучестью УВ, будет явно недостаточно для первичной миграции УВ (England et al., 1987).
Слайд 50С приближением к порогу миграции поровое давление достигает предела образования
микротрещин растяжения и поддерживаемое продолжающейся генерацией УВ сохраняется некоторое время
на этом уровне. Затем оно может релаксировать. В разрезе скв. 411 продолжающаяся генерация и хорошее качество ловушек поддерживают АВПД на уровне 1.6-1.7 от гидростатического давления. В осадочном разрезе Геологической площади Западно-Сибирского бассейна в районе скв. 35, аномальное давление релаксировало до гидростатического.Рост аномального порового давления в материнских породах баженовской свиты, перекрытых мощным (до 300 м) слоем глинистых сланцев ачимовской свиты, совпадает с началом заметной генерации жидких УВ.
Слайд 51Вторичный крекинг жидких УВ – источник АВПД
Ряд исследователей рассматривает генерацию
газа при крекинге жидких УВ как вероятный механизм образования АВПД
на больших глубинах. Крекинг нефти будет стартовать при температурах: T=120-140°C и завершается при температурах около 180°C. Единица объёма стандартной сырой нефти при крекинге дает 534.3 объёма газа (при стандартных Р-Т условиях) и небольшое количество графитового остатка. Расчеты показывают, что крекинг только 1% нефти способен повысить поровое давление до литостатического, т.е. превышающего предел гидрорастрескивания (Barker, 1990). Ряд примеров зон глубоких АВПД в юрских и триасовых резервуарах бассейна Северного моря и бассейнов Миссисипи и Алабама могут свидетельствовать о возможности такого механизма формирования зон АВПД.Слайд 52 Течение грунтовых вод и другие источники АВПД
Движение метеорных
вод под действием гидравлического напора может создавать аномалии давления в
неглубоких осадочных горизонтах с обильным обводнением. Для функционирования этого механизма требуется существование приподнятых структур, и латеральная непрерывность резервуаров под непрерывной покрышкой (Toupin et al., 1997).Восходящие движения пузырьков газа в несжимаемой жидкости теоретически также могут служить причиной заметных АПД, но до настоящего времени слабо изучены. Другой механизм, связанный с осмотическим давлением, может генерировать лишь незначительные аномальные давления в локальных местах, так как расчеты показывают, что в условиях осадочных бассейнов не существует эффективных осмотических мембран (Bradley, 1975; Osborne and Swarbrick, 1997).
Слайд 53Выводы
Возникновение зон АВПД относится к локальным событиям по времени и
месту своего проявления.
Даже при самых неблагоприятных условиях для миграции
флюидов время для снижения аномально высоких давлений до нормального гидростатического не должно превышать нескольких миллионов дет. Даже наличие мощных и надёжных покрышек не гарантирует от миграции через них флюидов в масштабе времени нескольких миллионов лет (Котровский, 1986).
Моделирование бассейнов, как правило, осуществляют, предполагая нормальный ход давления с заранее известной зависимостью пористости от давления или глубины. Это оправдано в свете недавних работ (Bolas et al., 2004). Показавших, что пористость пород в зонах АВПД часто практически не отличается от нормальной.
Возможное влияние отклонений, вызванных возникновением локальных зон АВПД, анализируется обычно в рамках приближённых решений.