Слайд 1Деревья: теория и практика использования
Слайд 2Шаблон класса бинарного дерева
template
class Tree {
struct Node
{
T item;
Node *left;
Node *right;
Node( const T& item,
Node *left = 0, Node *right = 0 ) {
Node::item = item;
Node::left = left;
Node::right = right;
};
public:
Node *root;
Tree() { root = 0; }
~Tree();
};
Слайд 3Дерево общего вида как бинарное
template
class Tree {
public:
struct
Node {
T item;
Node *son;
Node
*brother;
Node( const T& item,
Node *son = 0, Node *brother = 0 ) {
Node::item = item;
Node::son = son;
Node::brother = brother;
};
private:
Node *root;
public:
Tree() { root = 0; }
~Tree();
};
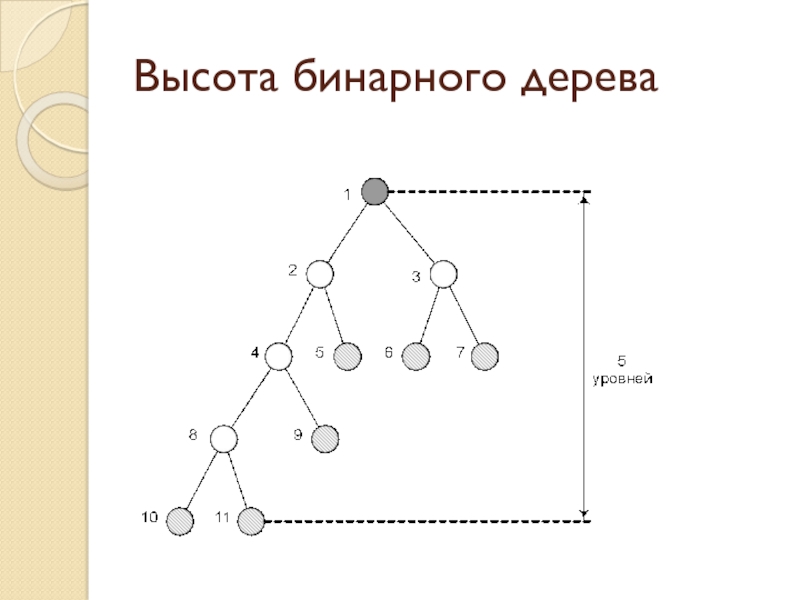
Слайд 5Формальное определение высоты дерева
Упражнение
Реализуйте рекурсивный алгоритм определения высоты дерева
Слайд 6Определение высоты дерева
template
int Tree::height() const {
if( root
== 0 ) return 0;
return root->height();
}
template
int Tree::Node::height()
const {
int max = 0;
for( Node *cur = son;
cur != 0;
cur = cur->brother ) {
int curHeight = cur->height();
if( curHeight > max ) max = curHeight;
}
return max+1;
};
Слайд 7Важные для практики частные случаи бинарных деревьев
Во многих случаях информация
о взаимном расположении узлов может определяться способом размещения древовидной структуры
в памяти
Удается обойтись без явных указателей на дочерние и родительские узлы
«Упакованное» бинарное дерево
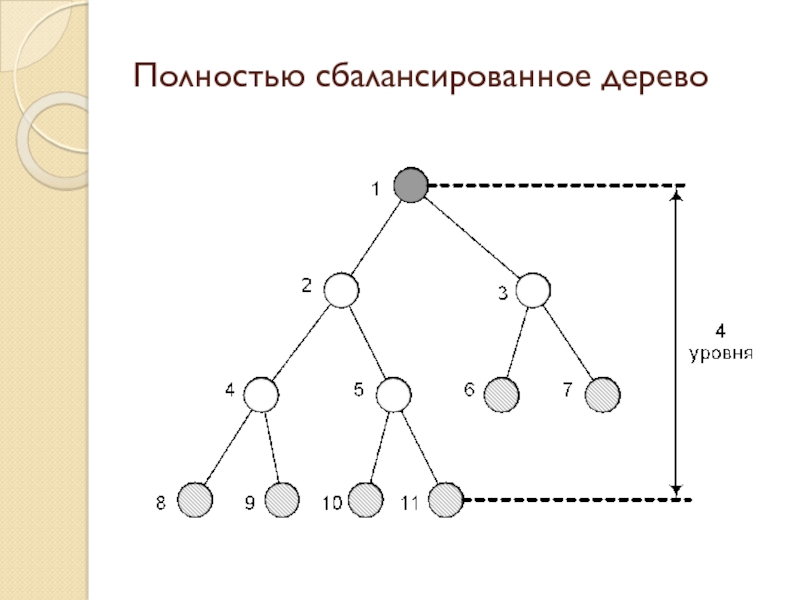
Слайд 8Полностью сбалансированное дерево
Слайд 9Хранение сбалансированного дерева в виде одномерного массива
Пусть r – номер
узла
Тогда номер родителя: r/2
Номер корня левого поддерева: 2r
Номер корня правого
поддерева: 2r+1
Индекс элемента в массиве: r-1
Дерево можно «упаковать» в одномерный массив и операции над узлами свести к операциям над индексами элементов массива
Слайд 10Просмотр от самого левого узла к самому правому
// Обработать бинарное
дерево из n узлов с
// корнем в узле noRoot
void
ProcessTree( int noRoot )
{
if( noRoot > n ) return; // выход из рекурсии
// Обработать левое поддерево
ProcessTree( noRoot*2 );
// Обработать корень дерева
// ...
// Обработать правое поддерево
ProcessTree( noRoot*2 + 1 );
}
Слайд 11Сортировка с использованием бинарного дерева (heap sort)
Другие названия: «сортировка сложным
выбором», «пирамидальная сортировка»
Алгоритм также использует обработку «упакованного» бинарного дерева
В основе
– понятие пирамиды:
Для любого узла r, имеющего одного потомка, справедливо:
Для любого узла r, имеющего двух потомков,
справедливо:
Слайд 12Пирамидальная сортировка: свойства пирамиды
Таким образом, корневая вершина поддерева, являющегося пирамидой,
содержит, соответствует наибольшему значению ключа в этом поддереве
Любой лист дерева
является пирамидой по определению
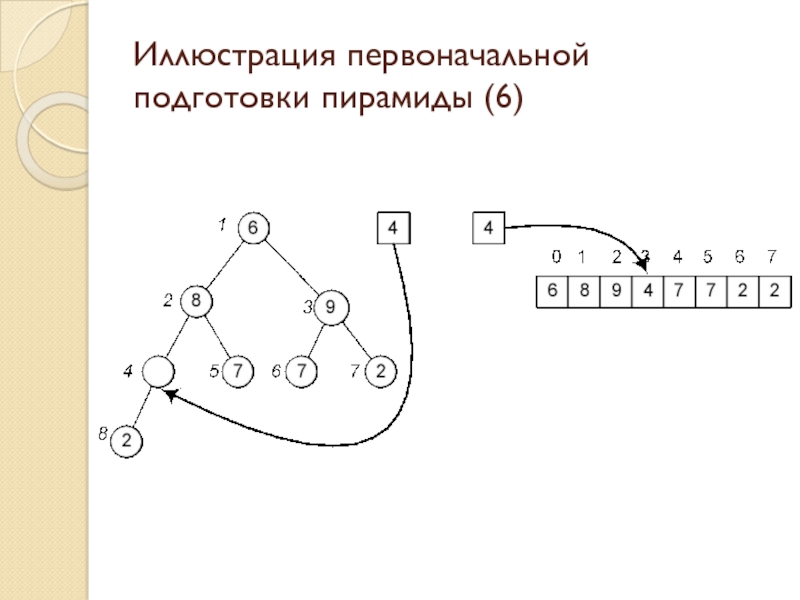
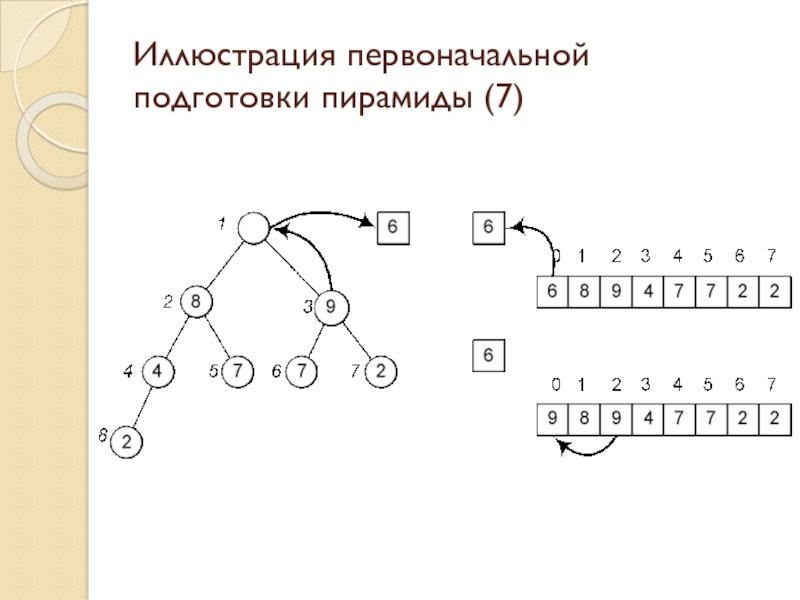
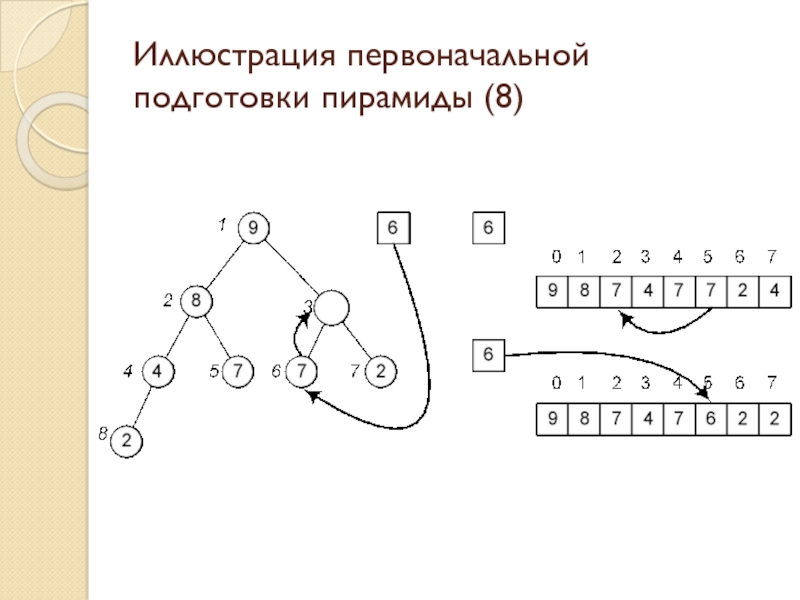
Слайд 13Пирамидальная сортировка: описание процесса сортировки
for( last = n; // Номер
последнего узла
// в начале равен n
last > 0; // Продолжаем, пока не рассмотрели
// все узлы
last-- )
{
// Поменять местами узлы с номерами
// 1 (корневой) и last
// ...
// Восстановить пирамиду из дерева с узлами
// от 1 до last-1 (просеивание)
// ...
}
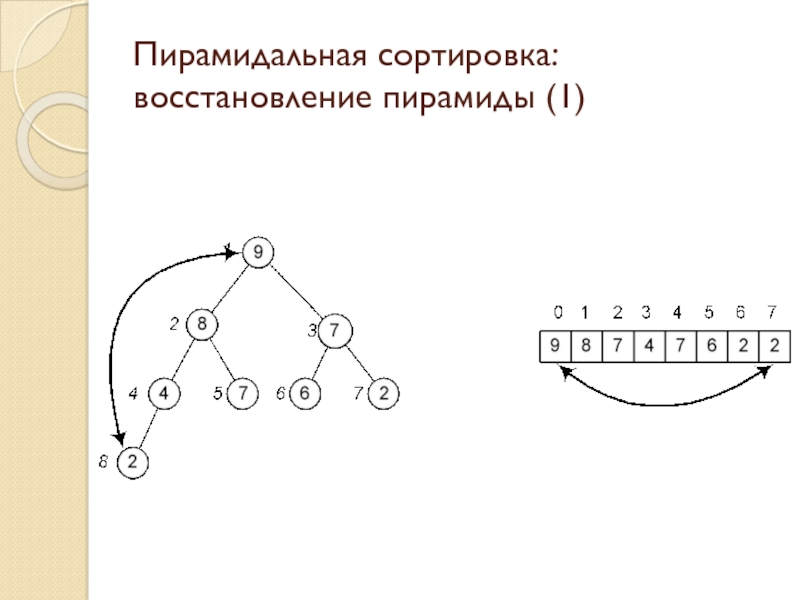
Слайд 14Пирамидальная сортировка: восстановление пирамиды (1)
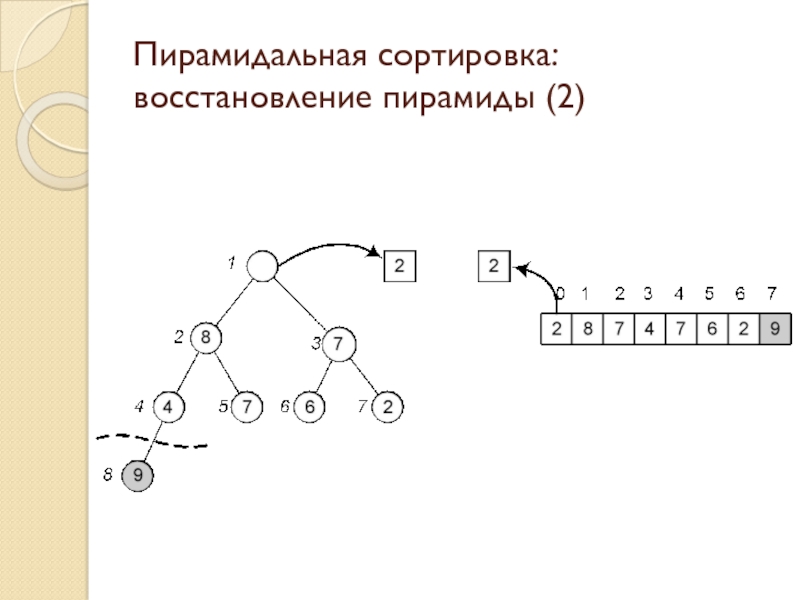
Слайд 15Пирамидальная сортировка: восстановление пирамиды (2)
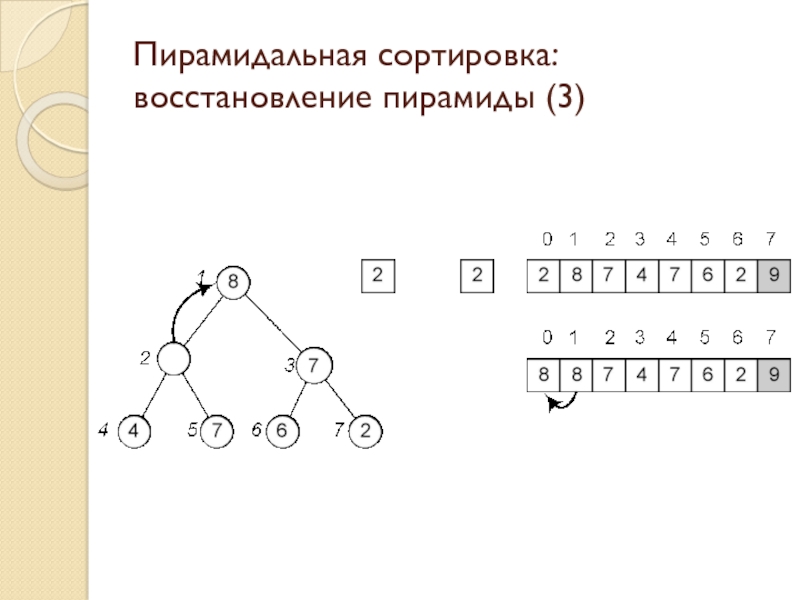
Слайд 16Пирамидальная сортировка: восстановление пирамиды (3)
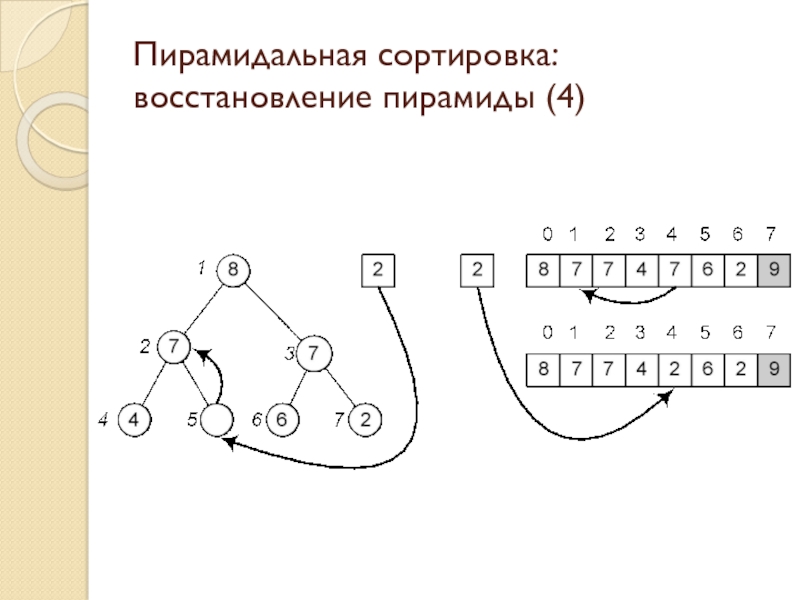
Слайд 17Пирамидальная сортировка: восстановление пирамиды (4)
Слайд 18Пирамидальная сортировка: функция просеивания «дыр»
template
void Sift( T *a,
int root, int last )
{
int hole = root;
T x = a[ hole-1 ];
for( ; ; )
{
int left = 2*hole;
int right = left + 1;
int pretender; // Номер претендента
if( left > last ) break; // Если лист –
// просеивание
// закончено
Слайд 19Пирамидальная сортировка: функция просеивания «дыр»
// Теперь
нужно выбрать
// претендента на заполнение
«дыры»
if( left == last ) pretender = left;
else
{
if( a[ left-1 ] < a[ right-1 ] )
pretender = right;
else pretender = left;
}
Слайд 20Пирамидальная сортировка: функция просеивания «дыр»
// Если
претендент не лучше x –
//
просеивание закончено
if( a[ pretender-1 ] < x ) break;
if( a[ pretender-1 ] == x ) break;
// Иначе: претендент заполняет «дыру»,
// при этом образуется новая «дыра»
a[ hole-1 ] = a[ pretender-1 ];
hole = pretender;
}
// Рано или поздно x «возвращается»
// в дерево
a[ hole-1 ] = x;
} // конец функции Sift
Слайд 21Что нужно для сортировки всей последовательности?
Подготовить пирамиду в самом начале
(это достигается за n/2 просеиваний)
Осуществить цикл из n-1 просеиваний, на
каждой итерации которого элемент с наибольшим значением ключа занимает свое окончательное место
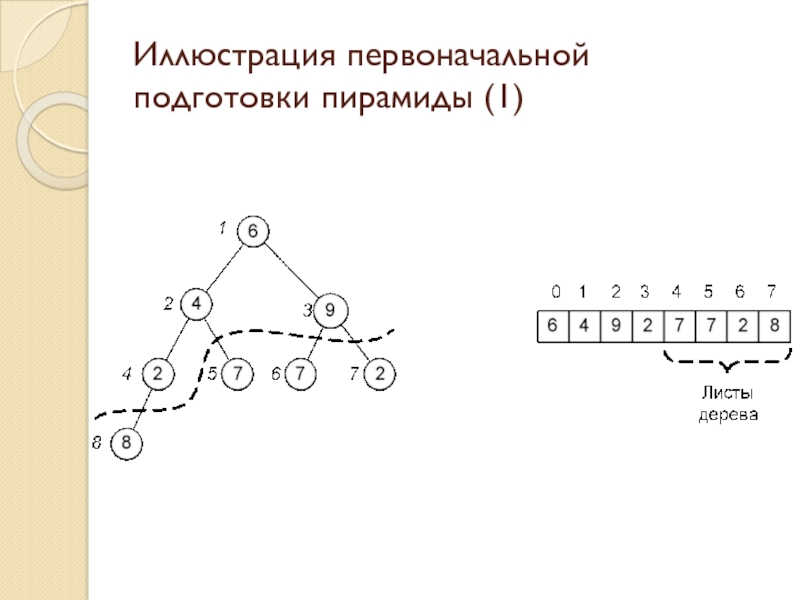
Слайд 22Иллюстрация первоначальной подготовки пирамиды (1)
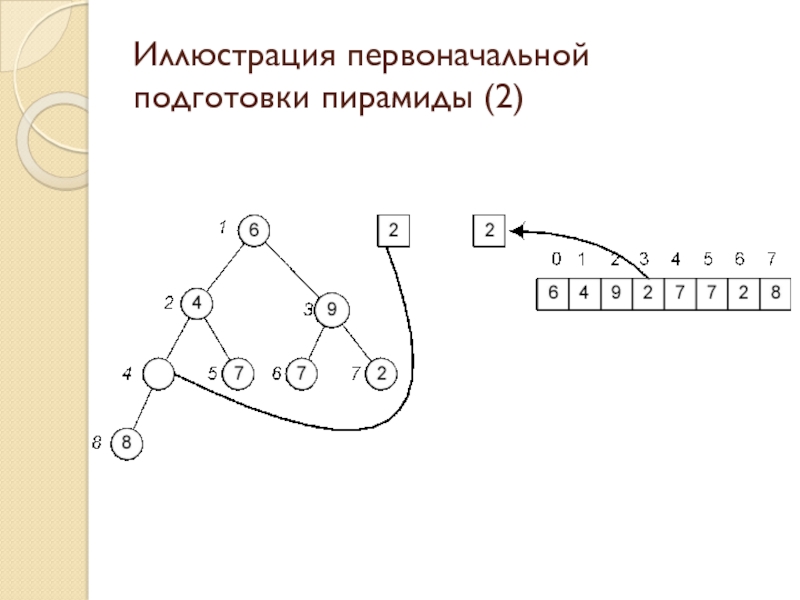
Слайд 23Иллюстрация первоначальной подготовки пирамиды (2)
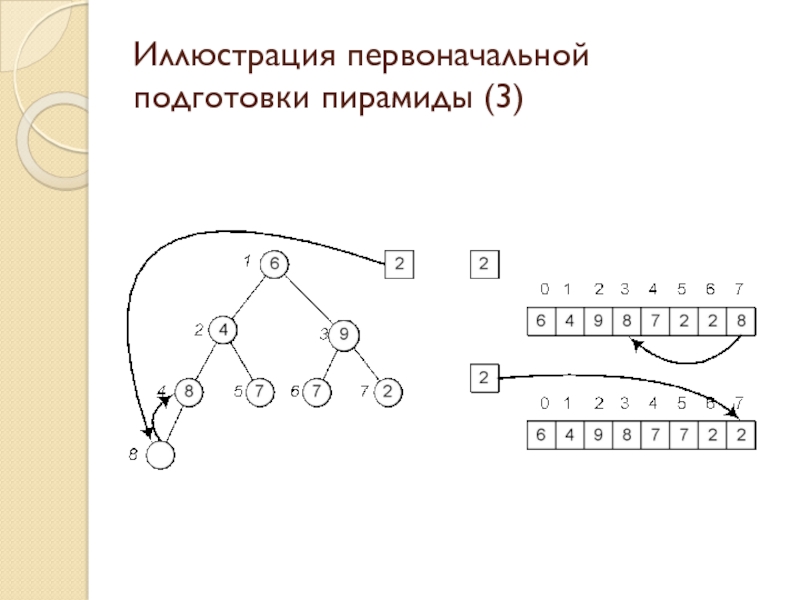
Слайд 24Иллюстрация первоначальной подготовки пирамиды (3)
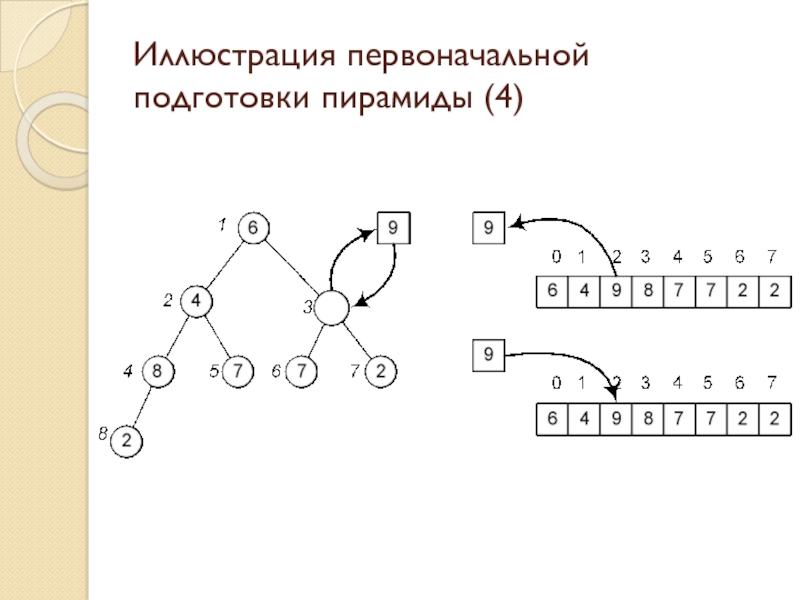
Слайд 25Иллюстрация первоначальной подготовки пирамиды (4)
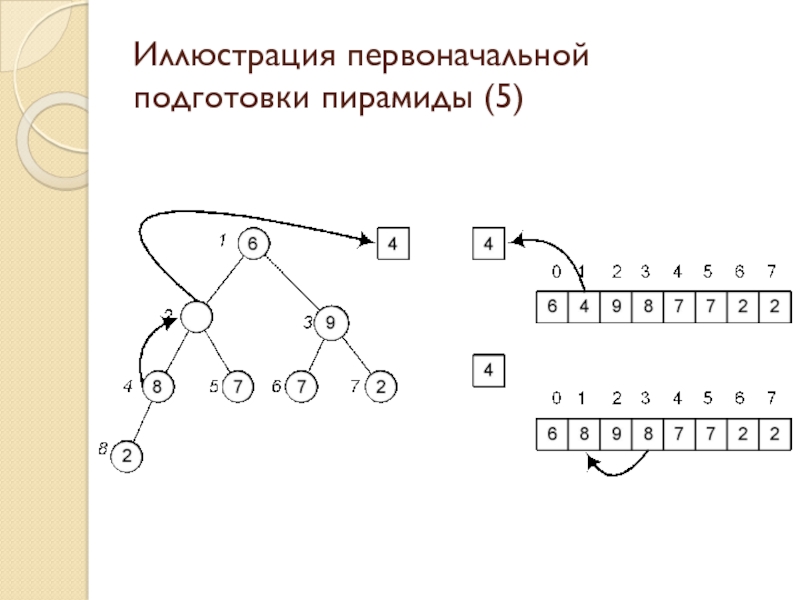
Слайд 26Иллюстрация первоначальной подготовки пирамиды (5)
Слайд 27Иллюстрация первоначальной подготовки пирамиды (6)
Слайд 28Иллюстрация первоначальной подготовки пирамиды (7)
Слайд 29Иллюстрация первоначальной подготовки пирамиды (8)
Слайд 30Пирамидальная сортировка: реализация
template
void HeapSort( T *a, int n
) {
int root, last;
// Первоначальная подготовка
пирамиды
for( root = n/2; root > 0; root-- )
Sift( a, root, n );
// Цикл сортировки
for( last = n; last > 1; last-- ) {
T copy = a[ 0 ];
a[ 0 ] = a[ last-1 ];
a[ last-1 ] = copy;
Sift( a, 1, last-1 );
}
}
Слайд 31Обход дерева
Левосторонний инфиксный обход
внутренний итератор
рекурсивная процедура
Нисходящий обход в глубину
внутренний итератор
стек,
хранящий информацию о непройденных поддеревьях
Нисходящий обход в ширину
внешний итератор
очередь
Восходящий обход
от корней к вершине
внешний итератор
стек
Слайд 32Для простоты используем:
template
class Tree {
struct Node {
T item;
Node *left;
Node *right;
Node( const T& item,
Node *left = 0, Node *right = 0 ) {
Node::item = item;
Node::left = left;
Node::right = right;
};
public:
Node *root;
Tree() { root = 0; }
~Tree();
};
Слайд 33template
class Actor {
public:
virtual void action( T& node)
= 0;
};
template
void Tree::traverseInfixLeft(Actor& a) {
recursiveInfixLeft( root, a
);
}
template
void Tree::recursiveInfixLeft( Node *node,
Actor& a ) {
if( node ) {
recursiveInfixLeft( node->left, a );
a.action( node->item );
recursiveInfixLeft( node->right, a );
}
}
// Левосторонний инфиксный обход
Слайд 34template
void Tree::traverseUpDown( Actor& a ) {
stack st;
Node *cur = root;
for( ; ; ) {
a.action( cur->item );
if( cur->right != 0 && cur->left != 0 ) {
st.push( cur->right );
cur = cur->left;
} else if( cur->left != 0 ) {
cur = cur->left;
} else if( cur->right != 0 ) {
cur = cur->right;
} else {
if( st.empty() ) break;
cur = st.top();
st.pop();
}
}
}
// Обход в глубину с использованием стека
Слайд 35template
void Tree::traverseInfixStack( Actor& a ) {
stack st;
Node *cur = root;
while( !st.empty() ) {
st.push(
cur );
if( cur->left != 0 ) {
cur = cur->left;
}
else do {
if( st.empty() ) break;
cur = st.top();
st.pop();
a.action( cur->item );
cur = cur->right;
} while( cur == 0 );
}
}
// Преобразование traverseInfixLeft с
// использованием стека
Слайд 36Коды Хаффмана
Сообщения состоят из символов
Вероятность появления символов – различная
Как закодировать
символы, чтобы уменьшить длину сообщения?
«Регулярный» код: просто, но не оптимально
Идея
– использовать код переменной длины
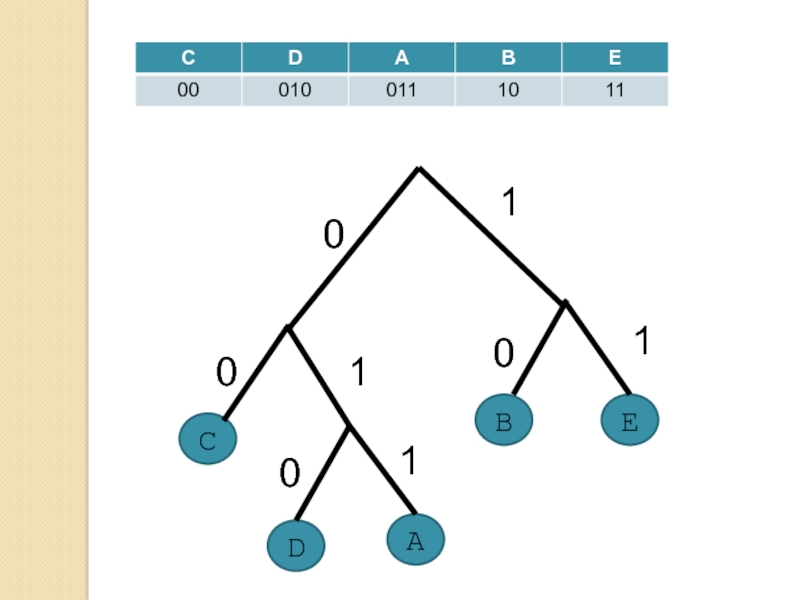
Префиксное свойство
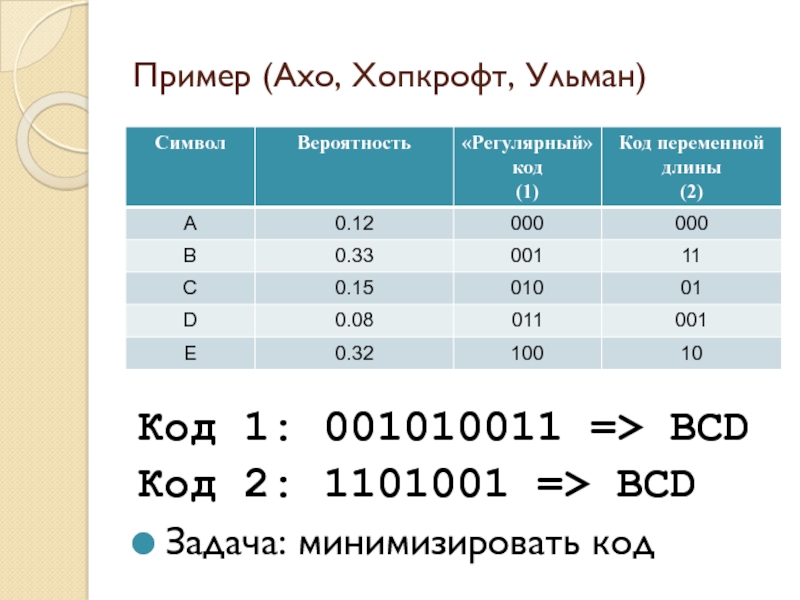
Слайд 37Пример (Ахо, Хопкрофт, Ульман)
Код 1: 001010011 => BCD
Код 2: 1101001
=> BCD
Задача: минимизировать код
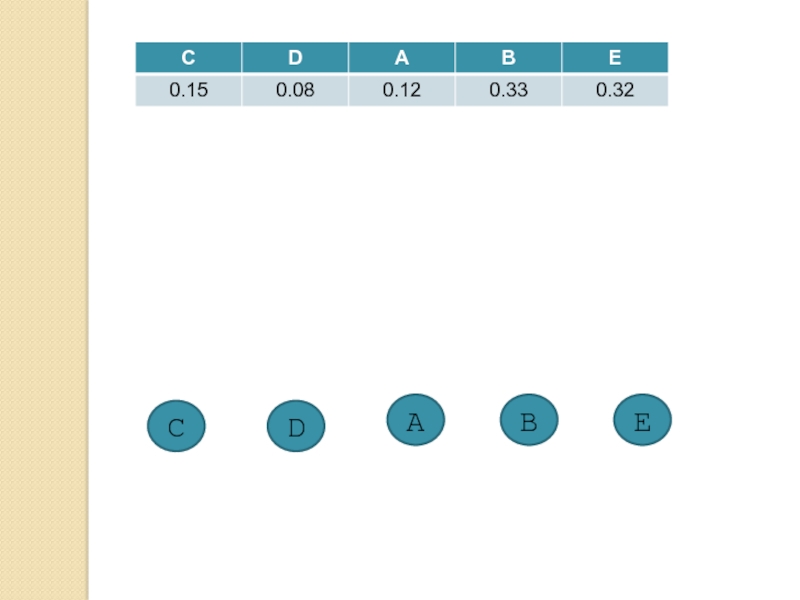
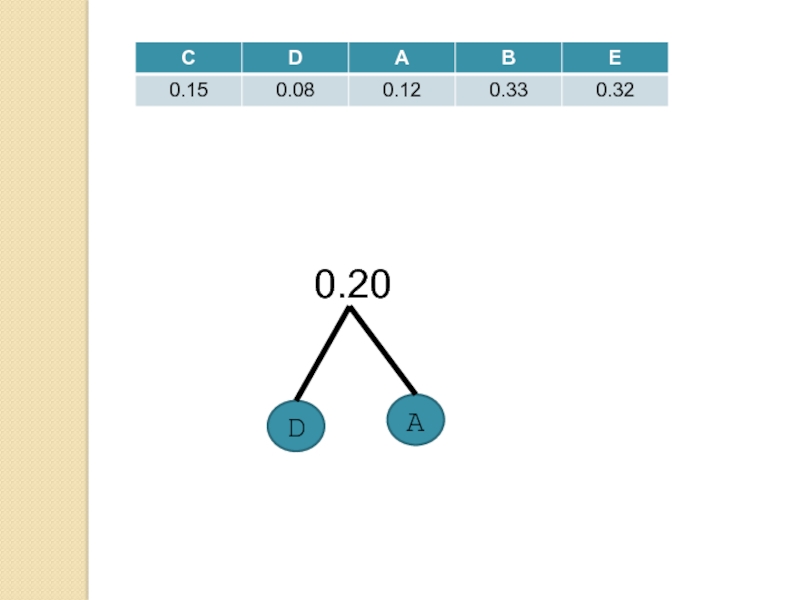
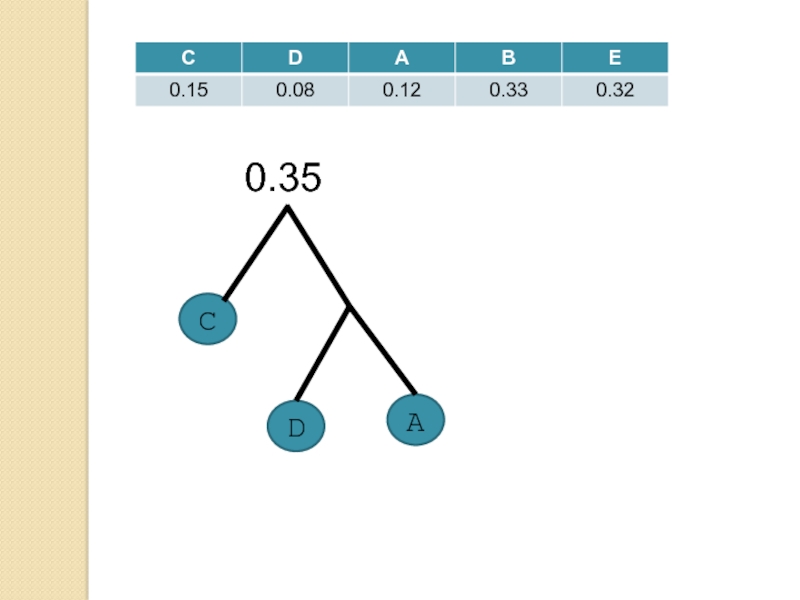
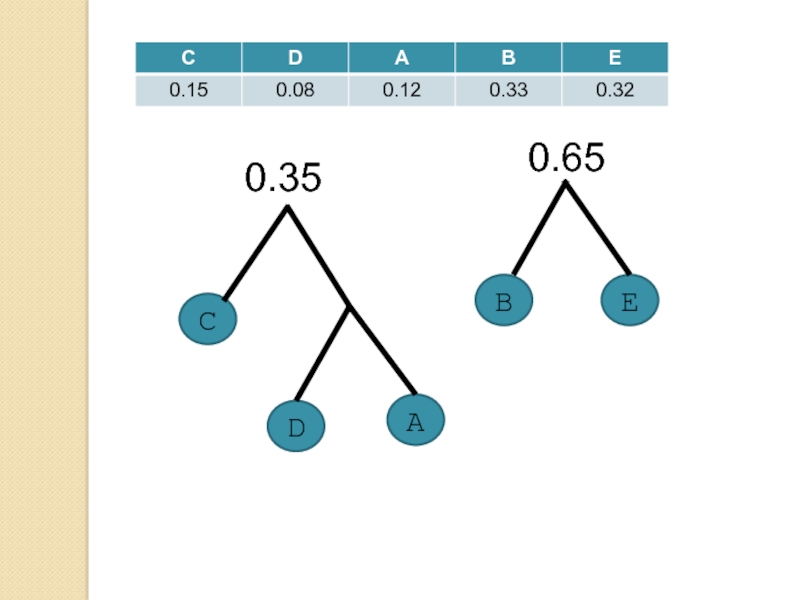
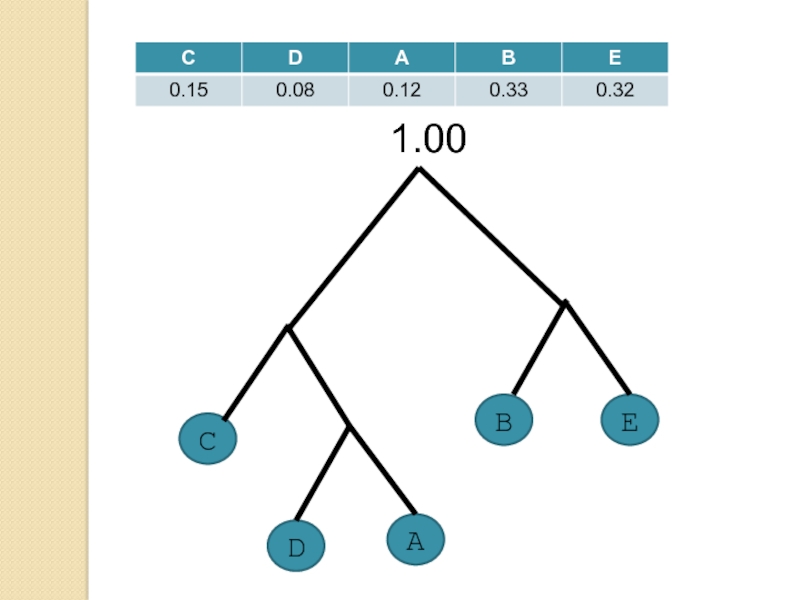
Слайд 38Алгоритм Хаффмана
Определение структуры дерева, представляющего используемый код
Построение леса из деревьев
путем объединения листьев, соответствующих кодам с наименьшими вероятностями