Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Диагонализация больших матриц Инвариантные подпространства. Матрица Рэлея.
Содержание
- 1. Диагонализация больших матриц Инвариантные подпространства. Матрица Рэлея.
- 2. Постановки задачРазмерность узельного базиса для бозе-системы из
- 3. Пространства и инвариантные подпространстваСкалярное произведение двух вещественных
- 4. Матрица РэлеяПусть Q=(q1,q2,…,qm) – векторы ортонормированного базиса
- 5. Процедура Рэлея – РитцаПроцедура Рэлея – Ритца
- 6. Подпространство КрыловаПодпространство Крылова для произвольного ненулевого вектора
- 7. Алгоритм ЛанцошаСтартовый вектор b выбирается либо в
- 8. Алгоритм ЛанцошаПары Ритца, аппроксимирующие собственные пары матрицы
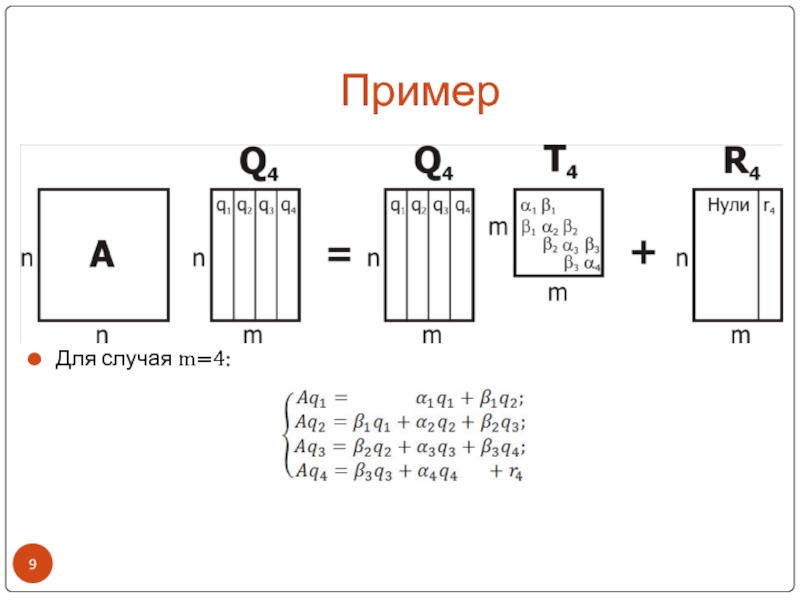
- 9. ПримерДля случая m=4:
- 10. ПримерМатрица T – трехдиагональная. Из ее определения получаем:Рекуррентные соотношения:В случае i=m определяется вектор невязки:
- 11. Скачать презентанцию
Постановки задачРазмерность узельного базиса для бозе-системы из 12 узлов и 12 частиц:при решении квантовых многочастичных задач редко приходится вычислять все собственные пары (собственный вектор и отвечающее ему собственное значение) гамильтоновой матрицыОбычные
Слайды и текст этой презентации
Слайд 1Инвариантные подпространства. Матрица Рэлея. Процедура Рэлея – Ритца. Подпространство Крылова. Алгоритм
Ланцоша
Слайд 2Постановки задач
Размерность узельного базиса для бозе-системы из 12 узлов и
12 частиц:
при решении квантовых многочастичных задач редко приходится вычислять все
собственные пары (собственный вектор и отвечающее ему собственное значение) гамильтоновой матрицыОбычные постановки задач:
Вычисление некоторых собственных значений, принадлежащих некоторому интервалу, или крайних собственных значений (например, низ спектра)
Нахождение некоторых собственных пар
Определение всех собственных значений или большого их количества без вычисления собственных векторов
Одним из самых мощных методов диагонализации симметричных матриц является алгоритм Ланцоша
Слайд 3Пространства и
инвариантные подпространства
Скалярное произведение двух вещественных векторов:
Линейная оболочка, натянутая на
векторы s1, s2, … :
Множество S называется образующим множеством подпространства
ΣОбразующее множество, содержащее наименьшее количество векторов, называется базисом подпространства, а количество векторов базиса называется размерностью подпространства
Если базисные векторы ортонормированны, то базис называется ортонормированным
Подпространство Σ инвариантно относительно A, если для любого вектора x из Σ следует, что вектор Ax также принадлежит Σ
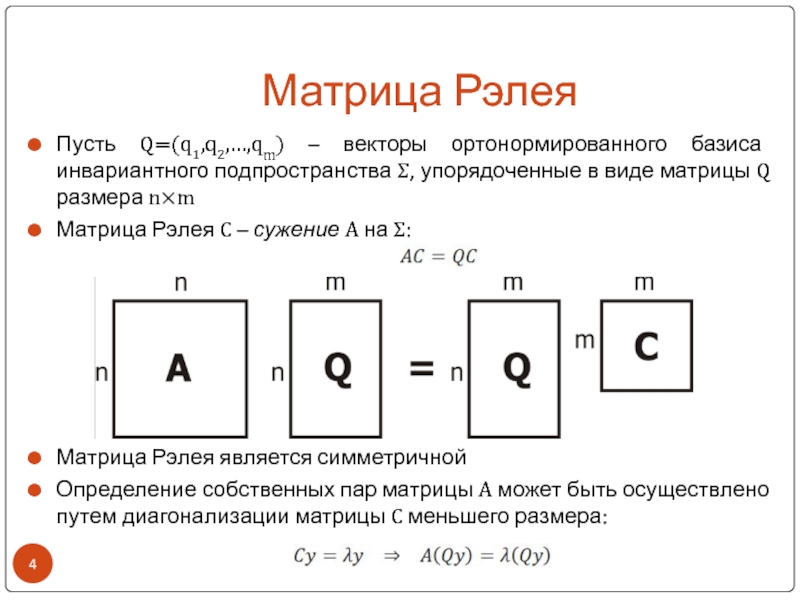
Слайд 4Матрица Рэлея
Пусть Q=(q1,q2,…,qm) – векторы ортонормированного базиса инвариантного подпространства Σ,
упорядоченные в виде матрицы Q размера n×m
Матрица Рэлея C –
сужение A на Σ:Матрица Рэлея является симметричной
Определение собственных пар матрицы A может быть осуществлено путем диагонализации матрицы C меньшего размера:
Слайд 5Процедура Рэлея – Ритца
Процедура Рэлея – Ритца обеспечивает наилучшее приближение
к собственным парам матрицы A
1. Ортонормализация матрицы Q, вычисление матрицы
РэлеяМатрица Рэлея H почти инвариантна относительно A
2. Определение требуемого количества собственны пар матрицы H:
3. Полученные значения Ритца ?? будут наилучшими приближениями к собственным значениям матрицы A, а векторы Ритца
– соответствующими приближениями к собственным векторам матрицы A
Слайд 6Подпространство Крылова
Подпространство Крылова для произвольного ненулевого вектора b:
При достаточно большом
m подпространство Крылова будет посчти инвариантно относительно A
В этом случае
матрица Рэлея является трехдиагональной, и вычисление пар Ритца существенно упрощаетсяСтолбцы матрицы Q могут быть связаны друг с другом с помощью трехчленных рекуррентных соотношений, позволяющих вычислять новые векторы базиса Q
Алгоритм Ланцоша обычно использует последовательность подпространств Крылова
и вычисляет пары Ритца матрицы A, отвечающие каждому из этих подпространств. Сходимость значений собственных пар обычно оказывается достаточно быстрой:
Слайд 7Алгоритм Ланцоша
Стартовый вектор b выбирается либо в произвольном виде, либо
с использованием априорной информации о собственных векторах матрицы A:
1. Пополнение
ортонормированного базиса:2. Вычисление промежуточной невязки:
3. Вычисление очередного диагонального элемента:
4. Завершение вычисления невязки:
5. Вычисление нормы невязки:
Слайд 8Алгоритм Ланцоша
Пары Ритца, аппроксимирующие собственные пары матрицы A:
Контроль сходимости –
норма вектора невязки:
Существуют версии алгоритма Ланцоша, предназначенные для отыскания крайних
собственных значений, некоторых внутренних собственных значений и даже всех собственных значений симметричных или эрмитовых матриц очень больших размеров, некоторые версии алгоритма позволяют вычислять и соответствующие собственные векторыПри практической реализации алгоритма Ланцоша возникают погрешности, связанные с машинной точностью обработки чисел двойной точности. Для решения этой проблемы разработаны специальные модификации алгоритма, производящие переортогонализацию векторов в зависимости от величины погрешности