Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
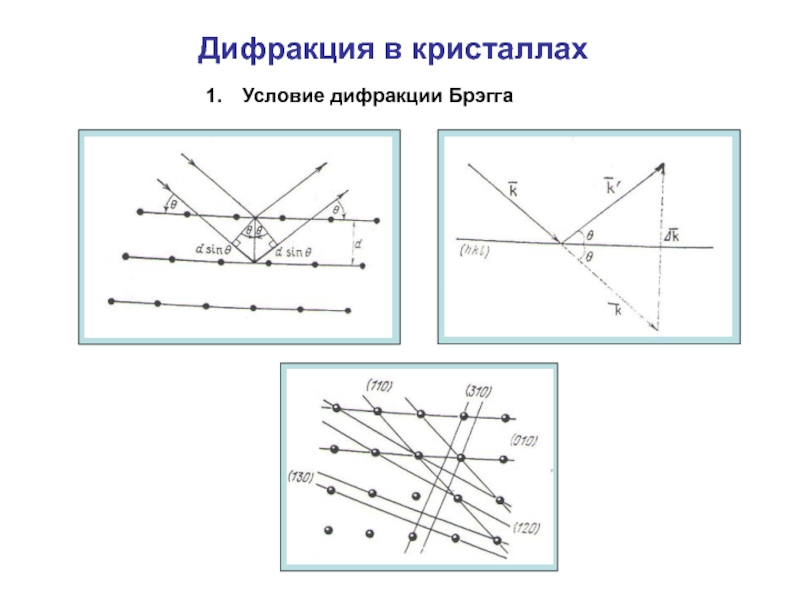
Дифракция в кристаллах
Содержание
- 1. Дифракция в кристаллах
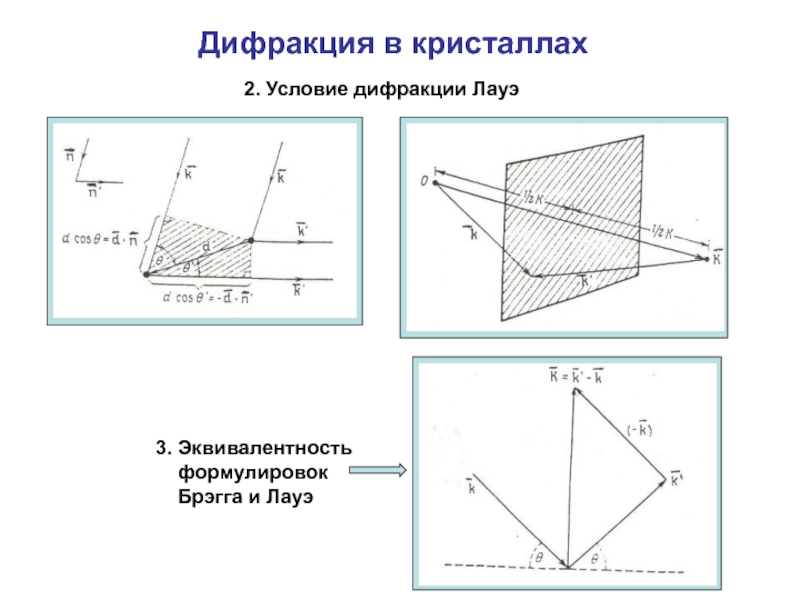
- 2. Дифракция в кристаллах2. Условие дифракции Лауэ3. Эквивалентность формулировок Брэгга и Лауэ
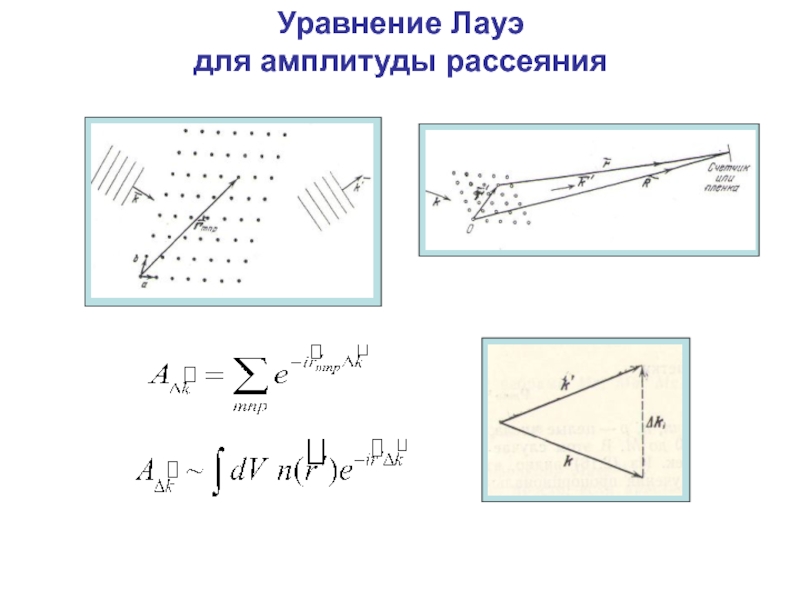
- 3. Уравнение Лауэ для амплитуды рассеяния
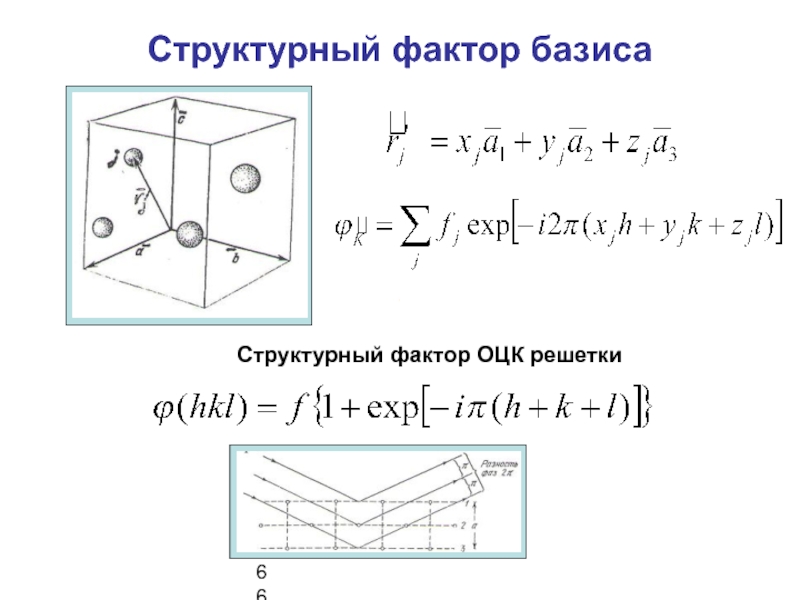
- 4. Структурный фактор базиса6666Структурный фактор ОЦК решетки
- 5. Структурный фактор ГЦК решетки6666
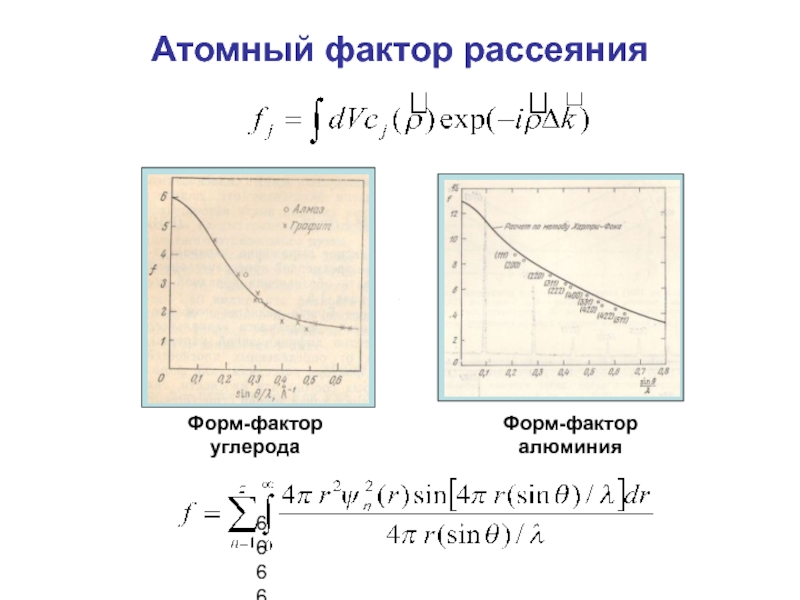
- 6. Атомный фактор рассеяния6666Форм-факторуглеродаФорм-фактор алюминия
- 7. Температурная зависимость линий отражения6666Множитель Дебая-УоллераТемпературная зависимостьинтенсивности дифракционныхмаксимумов (h00) для алюминия
- 8. Фактор поглощения6666Рентгеновское излучение, рассеянное кристаллом, значительно поглощается
- 9. Множитель Лорентца6666Реальные кристаллы являются мозаичными, т. е.
- 10. Интегральная интенсивность дифракционных максимумов6666С учетом всех
- 11. Экспериментальные методы рентгеновского спектроскопического анализа6666Построение ЭвальдаМонохроматическое излучение
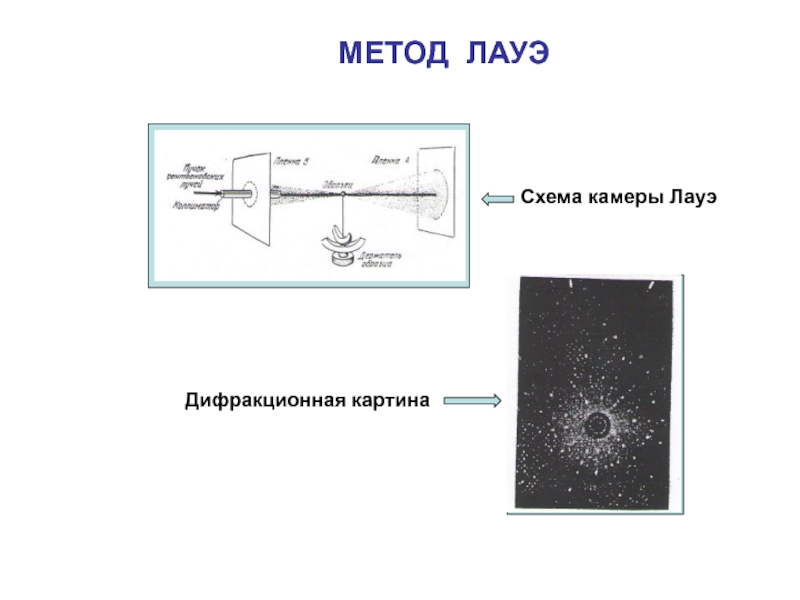
- 12. МЕТОД ЛАУЭСхема камеры ЛауэДифракционная картина
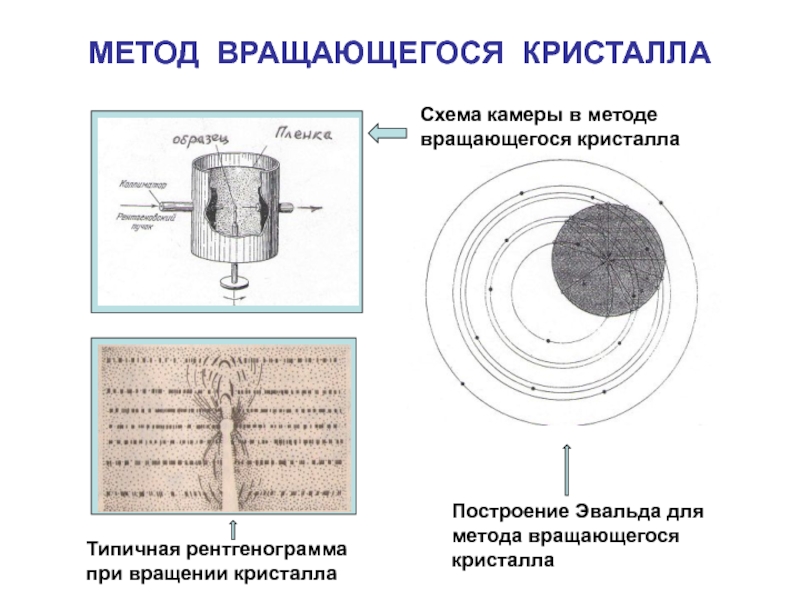
- 13. МЕТОД ВРАЩАЮЩЕГОСЯ КРИСТАЛЛАСхема камеры в методевращающегося кристаллаПостроение Эвальда дляметода вращающегося кристаллаТипичная рентгенограммапри вращении кристалла
- 14. МЕТОД ДЕБАЯ-ШЕРРЕРАСхема камеры в методе Дебая-ШеррераРентгенограммы
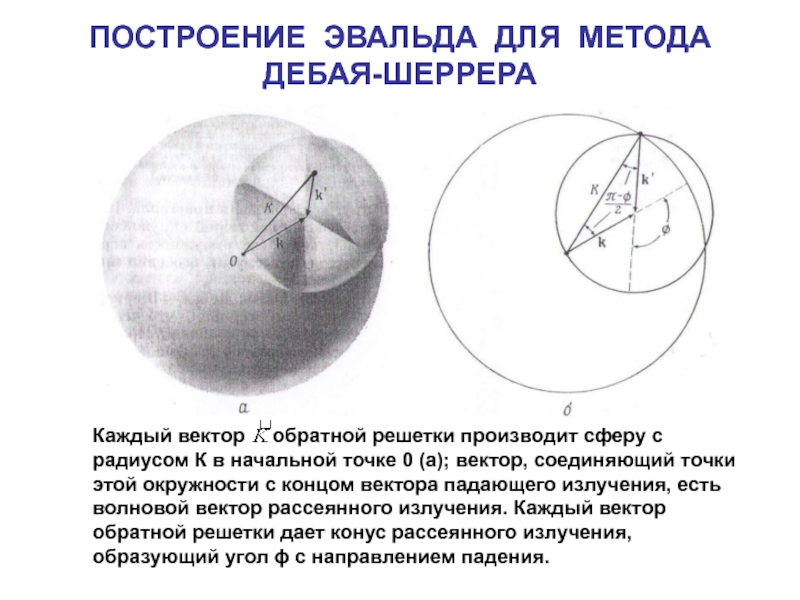
- 15. ПОСТРОЕНИЕ ЭВАЛЬДА ДЛЯ МЕТОДА ДЕБАЯ-ШЕРРЕРАКаждый вектор
- 16. Скачать презентанцию
Дифракция в кристаллах2. Условие дифракции Лауэ3. Эквивалентность формулировок Брэгга и Лауэ
Слайды и текст этой презентации
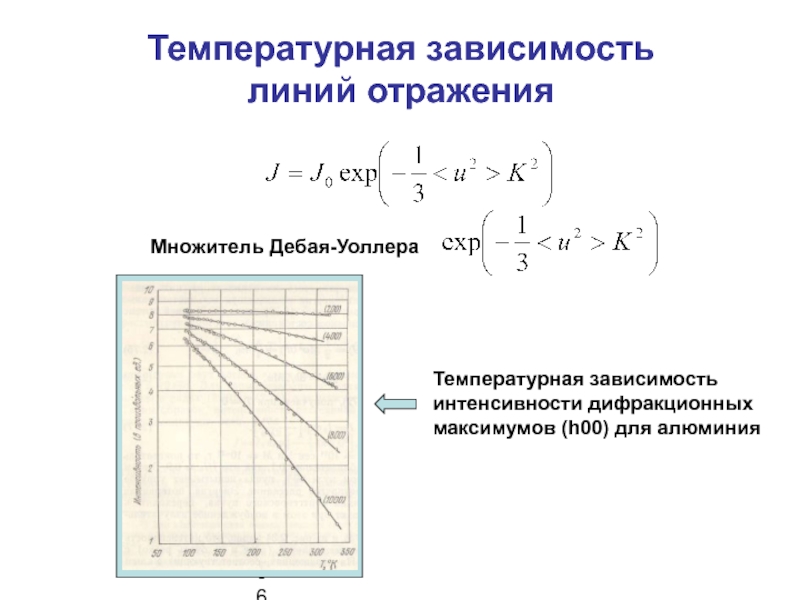
Слайд 7Температурная зависимость
линий отражения
6666
Множитель Дебая-Уоллера
Температурная зависимость
интенсивности дифракционных
максимумов (h00) для алюминия
Слайд 8Фактор поглощения
6666
Рентгеновское излучение, рассеянное кристаллом, значительно поглощается в нем. Поглощение
зависит от угла рассеяния , плотности вещества
и линейного коэффициента рассеяния . При расчете интенсивности поглощение учитывают, вводя в формулу множитель (фактор) поглощения .При получении рентгенограмм от поликристаллических образцов интенсивность дифракционных линий также зависит от вероятности нахождения кристаллитов в отражающем положении. Эта вероятность зависит от числа эквивалентных плоскостей {hkl}.
Число эквивалентных плоскостей р, называемое множителем (фактором) повторяемости, зависит от симметрии кристалла.
Так, для кубического кристалла р имеет следующие значения:
12 — для {110}, 8 — для {111} и 6 — для {100}.
Фактор повторяемости
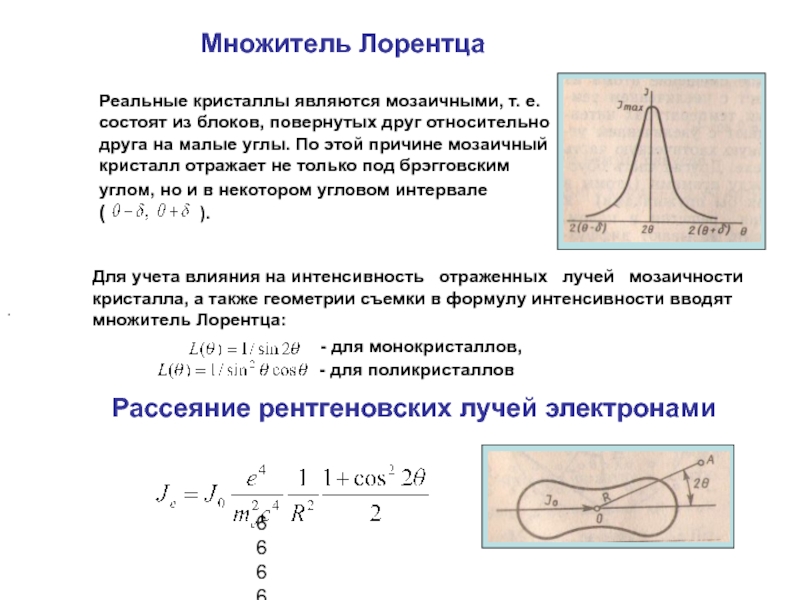
Слайд 9Множитель Лорентца
6666
Реальные кристаллы являются мозаичными, т. е. состоят из блоков,
повернутых друг относительно друга на малые углы. По этой причине
мозаичный кристалл отражает не только под брэгговским углом, но и в некотором угловом интервале ( ).Для учета влияния на интенсивность отраженных лучей мозаичности кристалла, а также геометрии съемки в формулу интенсивности вводят множитель Лорентца:
Рассеяние рентгеновских лучей электронами
- для монокристаллов,
- для поликристаллов
.
Слайд 10Интегральная интенсивность
дифракционных максимумов
6666
С учетом всех факторов формулы интегральной интенсивности
дифракционных максимумов для малых или мозаичных кристаллов имеют вид:
(для поликристаллов)
.
(для монокристаллов)
Слайд 11Экспериментальные методы рентгеновского спектроскопического анализа
6666
Построение Эвальда
Монохроматическое
излучение (λ = сonst)
Немонохроматическое излучение (
)
Слайд 13МЕТОД ВРАЩАЮЩЕГОСЯ КРИСТАЛЛА
Схема камеры в методе
вращающегося кристалла
Построение Эвальда для
метода вращающегося
кристалла
Типичная рентгенограмма
при вращении кристалла
Слайд 14МЕТОД ДЕБАЯ-ШЕРРЕРА
Схема камеры в методе Дебая-Шеррера
Рентгенограммы кремния, полученные методом
Дебая-Шеррера: а) на пленке; б) с помощью счетчика
а)
б)
Слайд 15ПОСТРОЕНИЕ ЭВАЛЬДА ДЛЯ МЕТОДА
ДЕБАЯ-ШЕРРЕРА
Каждый вектор обратной решетки производит
сферу с радиусом К в начальной точке 0 (а); вектор,
соединяющий точки этой окружности с концом вектора падающего излучения, есть волновой вектор рассеянного излучения. Каждый вектор обратной решетки дает конус рассеянного излучения, образующий угол ɸ с направлением падения.
