Слайд 1 Динамические многомерные модели (детерминированные).
Представление в пространстве состояний.
dx/dt = Ax
+ Bu + Гd; x(0) – начальные
условия
y = Cx
x - n-мерный вектор состояний;
u - m-мерный вектор управления;
d - k-мерный вектор возмущений;
y - -мерный вектор выхода;
А=[nn] Г=[nk]
В=[nm] С=[ln]
d
u x y
Модель «выход-вход»
вход выход - частотная область
L - преобразование Лапласа
Wp
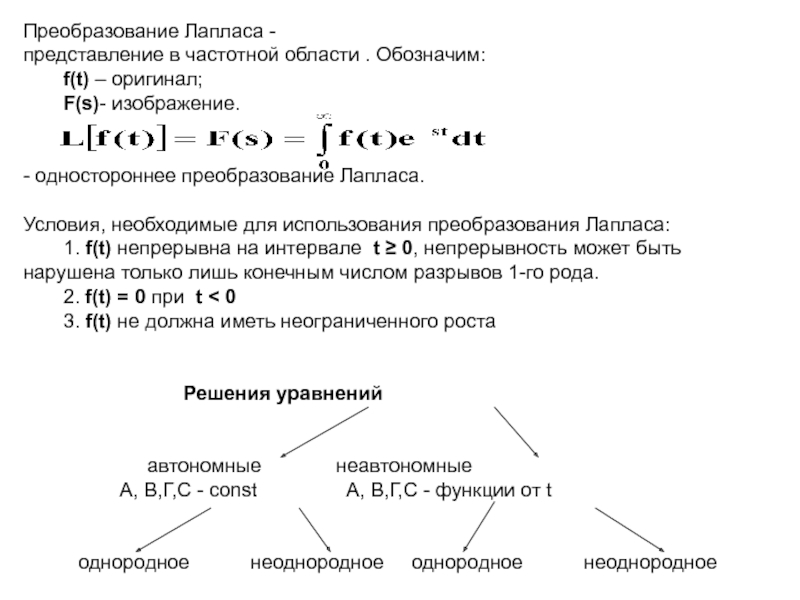
Слайд 2Преобразование Лапласа -
представление в частотной области . Обозначим:
f(t) – оригинал;
F(s)-
изображение.
- одностороннее преобразование Лапласа.
Условия, необходимые для использования преобразования Лапласа:
1. f(t) непрерывна на интервале t 0, непрерывность может быть нарушена только лишь конечным числом разрывов 1-го рода.
2. f(t) = 0 при t < 0
3. f(t) не должна иметь неограниченного роста
Решения уравнений
автономные неавтономные
А, В,Г,С - const А, В,Г,С - функции от t
однородное неоднородное однородное неоднородное
Слайд 3В задаче Коши x(t) = (x(0))- ф-ия от начальных условий
Задача Коши для автономных
e 1 + - элемент
чистого запаздывания
Скалярный случай
x(0) – начальные условия
Слайд 4Векторное решение(стационарное, однородное)
x(0) – начальные условия
- фундаментальная (переходная) матрица
Пусть
имеем
- произвольное начальное условие
x(0) - начальное условие
Свойства . Ф(t):
1.Ф(0) = eA0 = I
2.Ф(t) = Ф(t’)Ф(t0) , где t’= t - t0
3.Ф-1(t) = Ф(-t)
Слайд 5Векторный случай (стационарный, неоднородный)
Умножаем на e -At
Слайд 6
Cвязь уравнений переменных состояния
и переменных модели «выход – вход».
Для решения задач
синтеза системы управления необходимо представление моделей как в переменных состояния, так и в переменных выход/вход
1. Переход от временной к частотной области
- матричные передаточные функции (по управлению и возмущению)
y(S)
2. Переход от частотной области к временной.
По одной и той же передаточной функции можно построить целое семейство уравнений в пространстве состояний. Это происходит потому, что передаточная функция - это рациональная дробь, а числитель и знаменатель ее представлены в виде полиномов, часто имеющих общие корни. При сокращении нарушается эквивалентность представления.
Условиям однозначного перехода от частотной области к временной является выполнение условий управляемости и наблюдаемости.
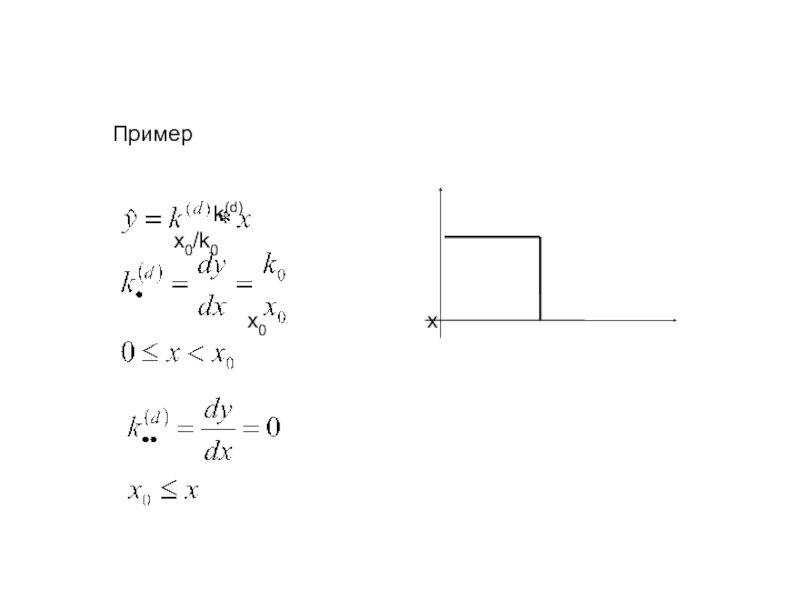
Слайд 8Пример
x(0) – начальные условия
A = MM-1
- преобразование подобия
- собственные числа;
M - матрица собственных
векторов.
- корни характеристического уравнения (инвариант);
e1 0
e2 0
e = e3
0 ...
en
x - n-мерный;
u - m-мерный .
Слайд 9 Управляемость.
Система называется полностью управляемой, если из любого начального состояния x(t0)
она может быть переведена в любое наперед заданное состояние с
помощью вектора управления u(t) за некоторое конечное время t - t0 0.
Для постоянных матриц A и B система может быть полностью управляемой тогда и только тогда, когда ранг матрицы Lc [nm] будет равен n(n – максимально возможное значение ранга такой матрицы).
Lc = [ B :AB:A2B: ... :An-1B]
[nm] [nm] [nm] [nm]
eAt в общем виде раскладывается в бесконечный ряд,
eAt = I + At +
для получения конечного результата используем теорему Гамильтона-Кэли. Представим eAt в виде конечного ряда
eAt = 0I + 1(At) + 2(At)2 + ... + n-1(At)n-1
Слайд 10Подставим это выражение под интеграл
О теореме Гамильтона- Кэли.
Всякая
квадратная матрица А удовлетворяет своему характеристическому уравнению.
Слайд 11Метод, основанный на этой теореме.
Пусть
Р(А)- многочлен от квадратной матрицы А
(nn), степень которого (многочлена) >n .
А - характеристический многочлен матрицы
А.
Р(А) /А = Q(A) + R(A) /А
Наблюдаемость
Система называется вполне наблюдаемой, если произвольное состояние x(t0) можно определить по информации u(t) и y(t) на конечном интервале t0 t t1
Для полной наблюдаемости линейных систем с постоянными матрицами необходимо и достаточно, чтобы ранг матрицы наблюдаемости L0 [nn] был бы равен n.
Слайд 12Некоторые критические советы.
Для практической реализации модели в пространстве
состояний и их анализа необходимо сделать следующее:
1. Анализ технологического процесса
объекта управления с определением переменных управления, управляющих воздействий, возмущений и выходных переменных.
2. Составление балансовых уравнений (материального и энергетического баланса).
3. Запись уравнений в отклонениях.
4. Линеаризация (например, в ряд Тейлора).
5. Переобозначение в привычных символах для модели в пространстве состояний.
6. Нахождение решения.
7. Анализ управляемости и наблюдаемости.
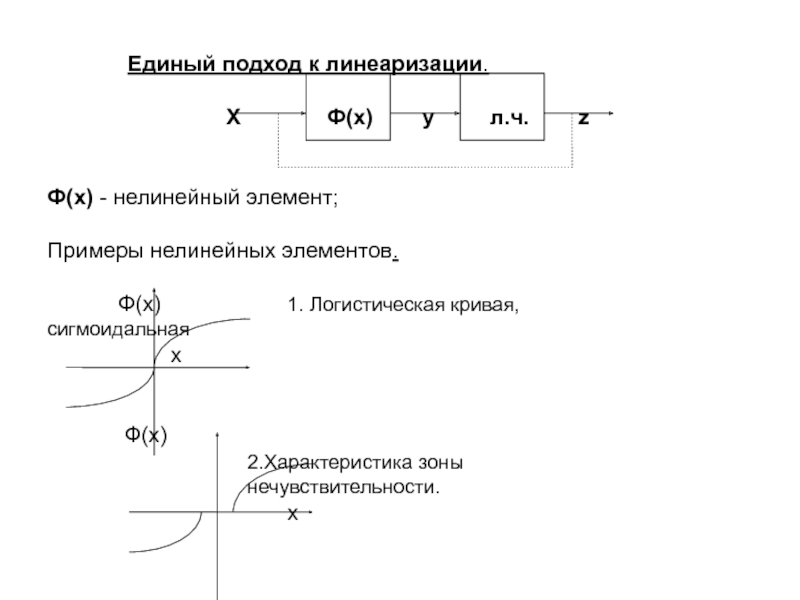
Слайд 13 Единый подход к линеаризации.
X
Ф(x) y л.ч. z
Ф(x) - нелинейный элемент;
Примеры нелинейных элементов.
Ф(x) 1. Логистическая кривая, сигмоидальная
x
Ф(x)
2.Характеристика зоны
нечувствительности.
x
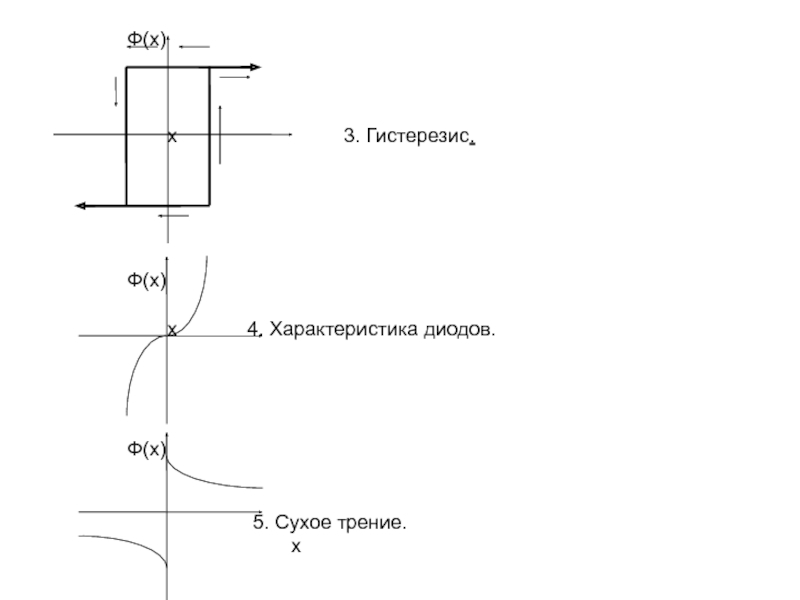
x 3. Гистерезис.
Ф(x)
x 4. Характеристика диодов.
Ф(x)
5. Сухое трение.
x
Слайд 15у= Ф(x) - нелинейная характеристика
- линеаризованная характеристика
1. K(s) - коэффициент статической
линеаризации
2. K(d) - коэффициент динамической (дифференциальной) линеаризации
3. K(h) -
коэффициент гармонической линеаризации
4. K(st) - коэффициент статистической линеаризации
Коэффициенты типа 1, 2 (k(s), k(d))
y = Ф(x)
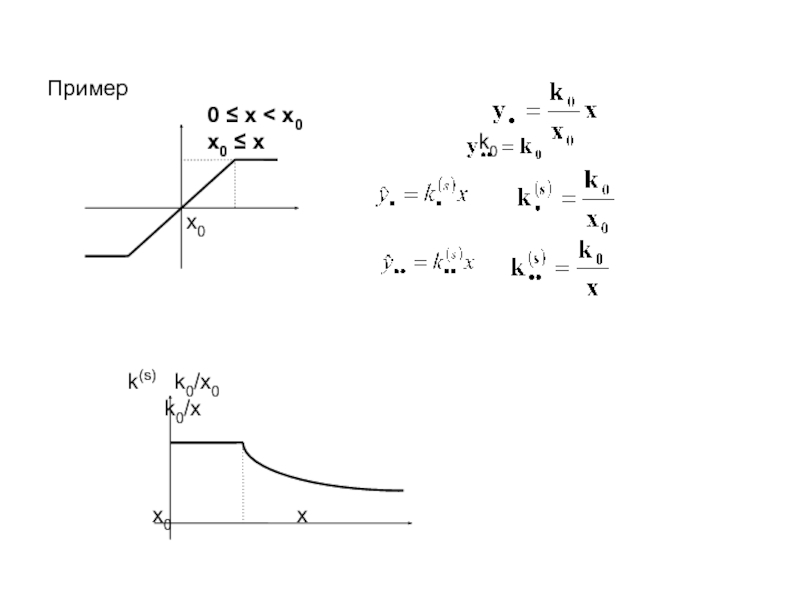
Слайд 16Пример
0 x x0
x0 x k0
x0
k(s) k0/x0
k0/x
x0 x
Слайд 18Коэффициенты типа 3 (k(h))
x(t) = Asin(t)
y =Ф(x)=Ф(Asin(t))
a).
б).
Слайд 20Используется при создании нелинейных систем уравнений.
Коэффициент k(st)
x(t)
Ф(x)
где x(t) - случайный процесс
Слайд 21Случайные процессы
Последовательность во времени любых данных, полученных в результате наблюдения
реального физического явления, можно классифицировать как детерминированные или недетерминированные процессы.
Детерминированные процессы – это процессы, которые можно описать явными математическими формулами.
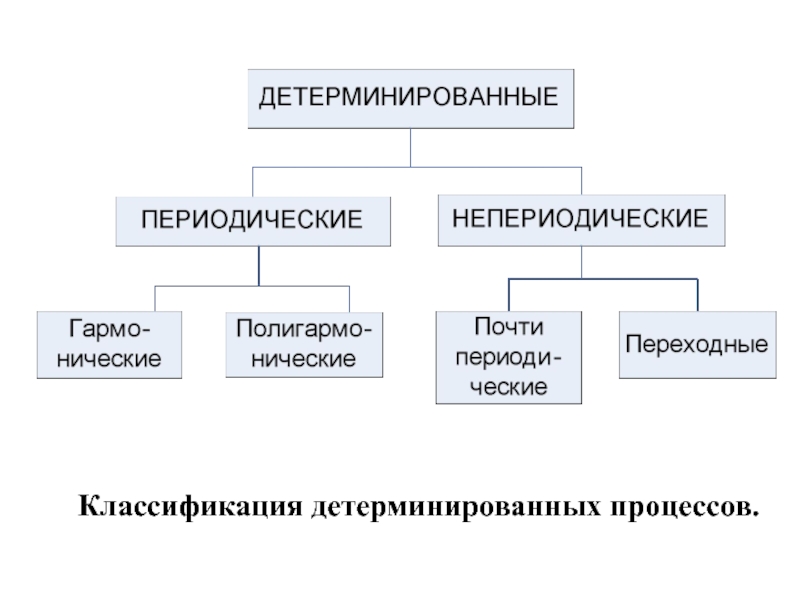
Классификация детерминированных процессов.
Процессы, описывающие детерминированные явления, делятся на периодические и непериодические.
В свою очередь периодические процессы можно разделить на гармонические и полигармонические. Непериодические процессы делятся на «почти периодические» и переходные.
Слайд 22 Классификация детерминированных процессов.
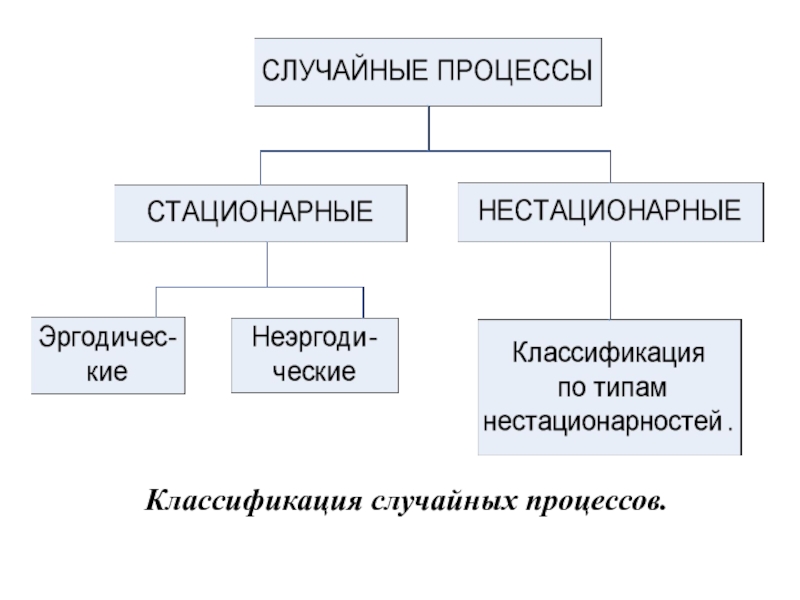
Слайд 23Классификация случайных процессов.
Конкретная реализация процесса, описывающего случайное явление, называется
выборочной функцией (или реализацией, если речь идет о наблюдении конечной
длительности).
Совокупность всех возможных выборочных функций, которые может дать изучаемое случайное явление, называется случайным или стохастическим процессом. Под реализацией случайного физического явления понимается один из возможных исходов случайного процесса.
Случайные процессы делятся на стационарные и нестационарные. В свою очередь стационарные случайные процессы делятся на эргодические и неэргодические.
Дальнейшая классификация нестационарных случайных процессов проводится по особенностям их нестационарностей.
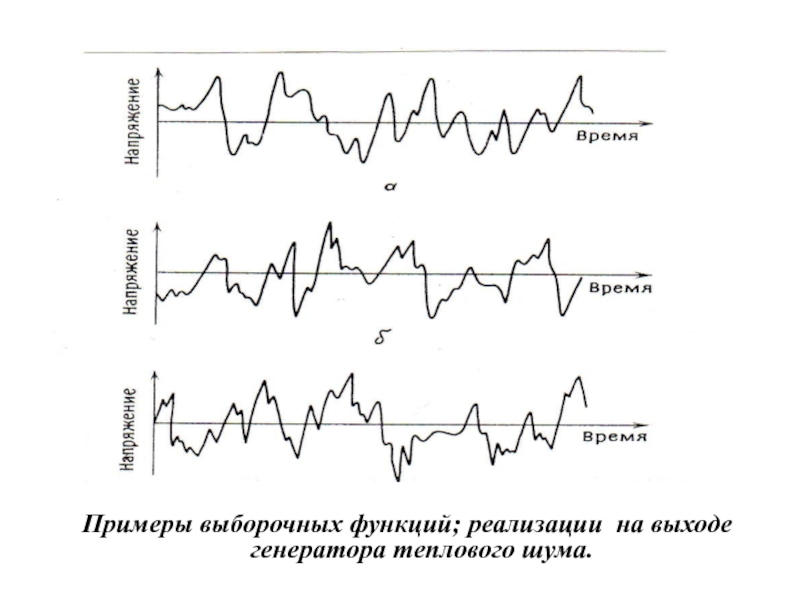
Слайд 24Примеры выборочных функций; реализации на выходе генератора теплового шума.
Слайд 25 Классификация случайных процессов.
Слайд 26Стационарные случайные процессы
Если физическое явление описывается случайным процессом, то свойство
этого явления можно оценить в любой момент времени путем усреднения
по совокупности выборочных функций, образующих случайный процесс.
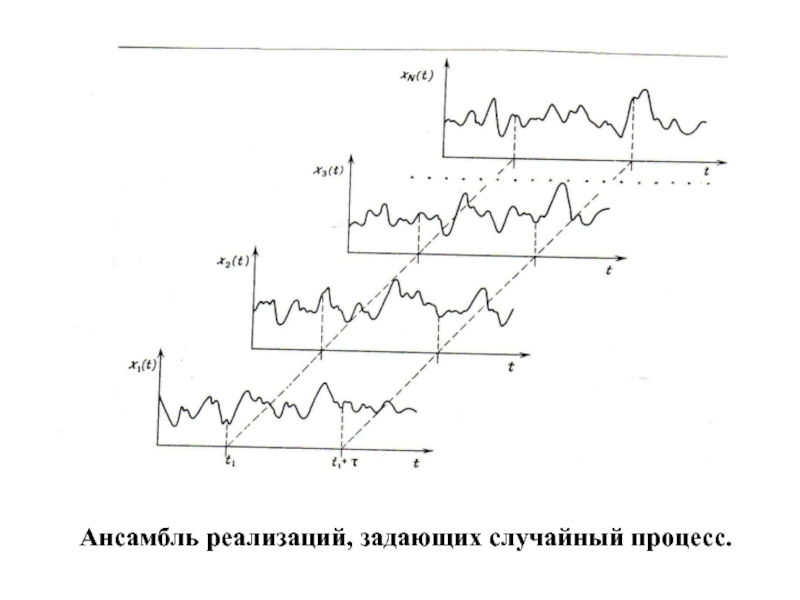
Рассмотрим, например, совокупность выборочных функций, называемую также ансамблем.
Среднее значение (первый момент) этого случайного процесса в момент времени t1 можно вычислить, взяв мгновенные значения всех выборочных функций ансамбля в момент времени t1 , сложив эти значения и разделив на число выборочных функций.
Аналогичным образом вычисляем ковариацию (смешанный момент) значений случайного процесса для двух различных моментов времени. Эта величина называется ковариационной функцией.
Слайд 27 Ансамбль реализаций, задающих случайный процесс.
Слайд 28Ковариационная функция вычисляется путем усреднения по ансамблю произведений мгновенных значений
в моменты времени t1 и t1+τ. Следовательно, среднее значение μх(t1)
и ковариационная функция
Rхх(t1, t1 +τ) случайного процесса {х(t)}, где символ { } обозначает ансамбль выборочных функций, определяется формулами, в которых суммирование производится в предположении равновероятности всех выборочных функций.
Слайд 29
В общем случае, когда μх(t1 ) и Rхх(t1, t1 +τ),
определенные уравнениями, зависят от момента времени t1, случайный процесс {х(t)}
называется нестационарным.
В том случае, когда μх(t1 ) и Rхх(t1, t1 +τ), не зависят от момента времени t1, случайный процесс называется слабо стационарным или стационарным в широком смысле.
Среднее значение слабо стационарного процесса постоянно, а ковариационная функция зависит только от сдвига времени τ,
т.е. μх(t1 )= μх и Rхх(t1, t1 +τ)= Rхх (τ).
Слайд 30Для определения полного набора функций распределения, задающих структуру случайного процесса
{х(t)}, нужно вычислить бесконечное число моментов и смешанных моментов высших
порядков.
В том случае, когда все моменты и смешанные моменты инвариантны во времени, случайный процесс {х(t)} называется строго стационарным или стационарным в узком смысле (не рассматривается случай, когда некоторые моменты распределения могут не существовать).
Во многих приложениях проверка слабой стационарности позволяет обосновать строгую стационарность.
Слайд 31Эргодические случайные процессы
В большинстве случаев характеристики стационарного случайного процесса
можно вычислить, усредняя по времени в пределах отдельных выборочных функций,
входящих в ансамбль. Возьмем, например, k-ю выборочную функцию ансамбля. Среднее значение μх(k ) и ковариационная функция Rхх(τ,k), вычисленные по k-й реализации равны
Слайд 32Если случайный процесс {х(t)}, стационарен, а μх(k) и Rхх(τ,k), вычисленные
по различным реализациям согласно формулам, совпадают, то случайный процесс называется
эргодическим.
Для эргодических процессов средние значения и ковариационные функции, полученные усреднением по времени (как и другие характеристики, вычисленные усреднением по времени), равны аналогичным характеристикам, найденным усреднением по ансамблю, т.е.
μх(k)= μх и Rхх(τ,k)= Rхх(τ).
Свойством эргодичности могут обладать только стационарные процессы.
Слайд 33
Эргодические случайные процессы образуют очень важный класс случайных процессов, поскольку
все свойства эргодических процессов можно определить
по единственной выборочной функции.
на
практике стационарные случайные процессы обычно оказываются эргодическими.
Именно по этой причине свойства стационарных случайных явлений часто можно определить по одной наблюдаемой реализации.
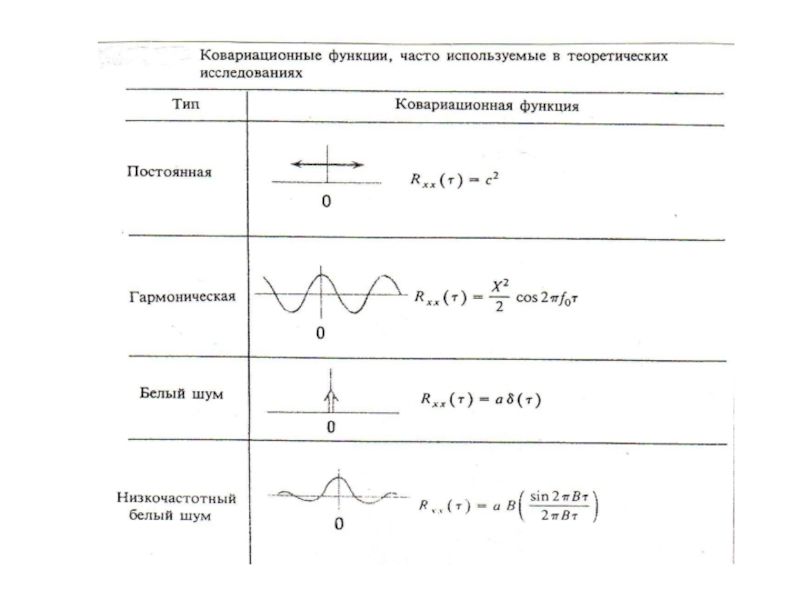
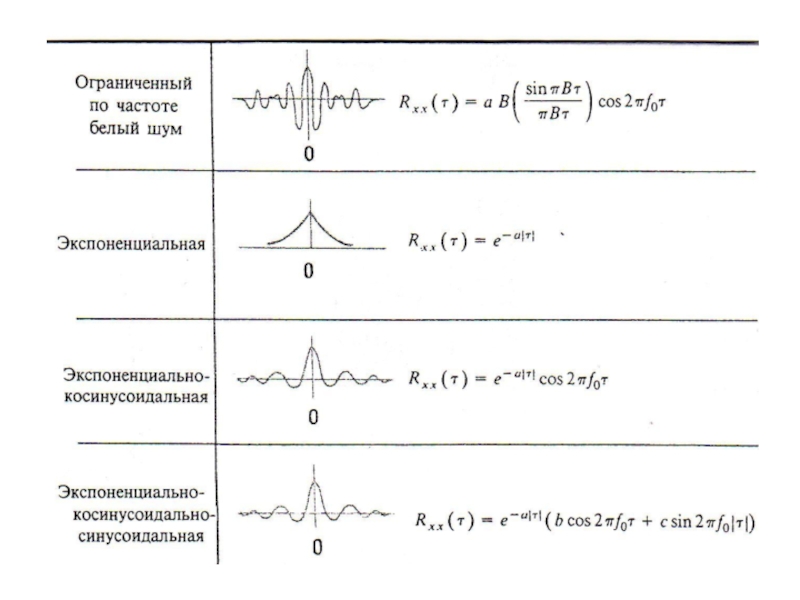
Слайд 34Примеры ковариационных функций
(наиболее часто используемые)
Итак, для стационарных случайных процессов
{xk(t)} и {yk(t)} средние значения постоянны и не зависят от
времени t, т.е. для всех t
где p(x) и p(y) – плотности вероятности случайных величин xk(t) и yk(t) соответственно. Корреляционные функции стационарных процессов также не зависят от t.
Слайд 35Ковариационные функции
Определим для произвольных и фиксированных t и τ функции
Величины
Rxx(τ) и Ryy(τ) называются автокорреляционными или ковариационными функциями процессов {xk(t)}
и {yk(t)} соответственно,
а Rxy(τ) называется взаимной ковариационной функцией {xk(t)} и {yk(t)} .
Слайд 36Ковариационные функции
Для двух стационарных случайных процессов {xk(t)} и {yk(t)} совместная
плотность вероятности p(x1,x2) пары случайных величин x1=xk(t) и x2=xk(t+τ) не
зависит от t. Совместная плотность вероятности p(y1 ,y2), относящаяся к паре случайных величин y1=yk(t) и y2=yk(t+τ), тоже не зависит от t. Этим же свойством обладает совместная плотность вероятности p(х1х2), характеризующая случайные величины x1=xk(t) и y2=yk(t+τ).В терминах этих плотностей имеем
Слайд 37Ковариационные функции
Из предположения стационарности следует, что ковариационные функции Rxx(τ) и
Ryy(τ) – четные функции от τ, т.е.
Rxx(-τ)=Rхх(τ), Ryy(-τ)=Ryy(τ).
В то
же время взаимная ковариационная функция не обладает свойством четности или нечетности , но удовлетворяет соотношению
Rxy(-τ)= Ryx(τ).
Слайд 38Белый шум
Белый шум - стационарный шум, спектральные составляющие которого равномерно
распределены по всему диапазону задействованных частот (классический пример-шум близкого водопада;
отдаленный шум водопада - розовый так как высокочастотные составляющие звука затухают в воздухе сильнее низкочастотных).
Название происходит от белого света. «Чисто» белый шум-идеализация.
Термин применяется к сигналу, имеющему автокорреляционную функцию, математически описываемую дельта – функцией Дирака по всем измерениям многомерного пространства, в котором этот сигнал рассматривается. Сигналы, обладающие этим свойством, могут рассматриваться как белый шум и определяют основное статистическое свойство.
Белый шум некоррелирован по времени (или по другому аргументу), не определяет его значений во временной области . Наборы, принимаемые сигналом, могут быть произвольными с точностью до главного статистического свойства (однако постоянная составляющая такого сигнала должна быть равна нулю).
Пример - двоичный сигнал, который может принимать только значения, равные нулю или единице, будет являться белым шумом только если последовательность нулей и единиц будет некоррелирована.
Дискретный белый шум — это просто последовательность независимых (то есть статистически не связанных друг с другом) чисел. Генератор белого шума использует метод псевдослучайных чисел (пакет Visual C++). Тогда , дискретный белый шум можно получить так:
x[i] = 2 * ((rand()/((double)RAND_MAX)) — 0.5)
В данном случае x — массив дискретного белого шума (без нулевой частотной составляющей), имеющего равномерное распределение от −1 до 1.

Слайд 39Белый шум
Гауссовский шум - шум с нормальным распределением по амплитуде,
который не эквивалентен белому шуму. Гауссовый шум предполагает распределение значений
сигнала в виде нормального распределения, тогда как термин «белый» имеет отношение к корреляции сигнала в два различных момента времени (эта корреляция не зависит от распределения амплитуды шума).
(В электронной музыке белый шум используется как в качестве одного из инструментов музыкальной аранжировки, так и в качестве входного сигнала для специальных фильтров, формирующих шумовые сигналы других типов, в частности, для воссоздания звучания ударных инструментов , тарелки).
Белый шум используется для измерения частотных х-к различных линейных динамических систем таких как усилители, электронные фильтры, дискретные системы управления, счетчики и т. д. При подаче на вход такой системы белого шума, на выходе получаем сигнал, являющийся откликом системы на приложенное воздействие. Ввиду того, что АФЧХ линейной системы есть отношение преобразования Фурье выходного сигнала к преобразованию Фурье входного сигнала, получить эту характеристику математически достаточно просто, причём для всех частот, для которых входной сигнал можно считать белым шумом.
Белый шум используется для генерирования случайных чисел и случайных последовательностей. Вектор случайных чисел является последовательностью отсчётов белого шума, когда его среднее значение и автокорреляционная матрица удовлетворяют следующим равенствам:
Итак,имеем вектор случайных чисел с нулевым средним значением и автокорреляц. матрицу в виде диагональной матрицы с дисперсиями по главной диагонали.

Слайд 40Белый случайный процесс (белый шум).
Непрерывный во времени случайный процесс
является
белым шумом тогда и только тогда, когда математическое ожидание
и автокорреляционная функция удовлетворяют следующим равенствам соответственно:
Т.е. это - случайный процесс с нулевым математическим ожиданием, имеющий автокорреляционную функцию, являющуюся дельта -функцией – функцией Дирака.
Такая автокорреляционная функция предполагает следующую спектральную плотность мощности:
так как преобразование Фурье дельта-функции равно единице на всех частотах. Ввиду того, что спектральная плотность мощности одинакова на всех частотах, белый шум и получил своё название (по аналогии с частотным спектром белого света).
Слайд 43Приведение к каноническому виду уравнений с частными производными в случае
двух независимых переменных