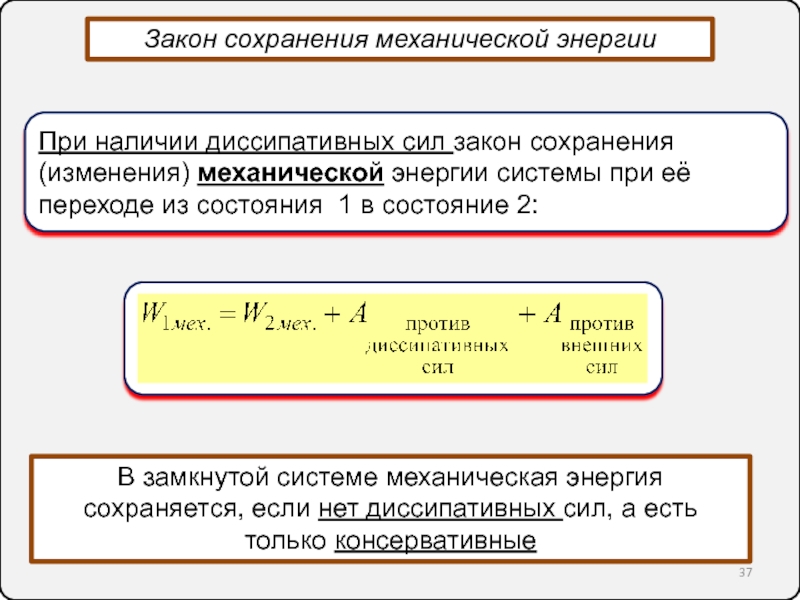
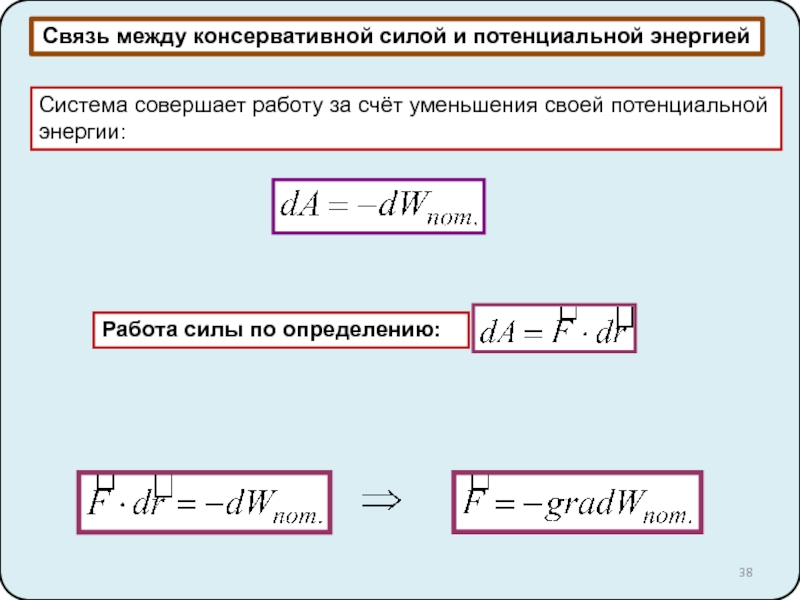
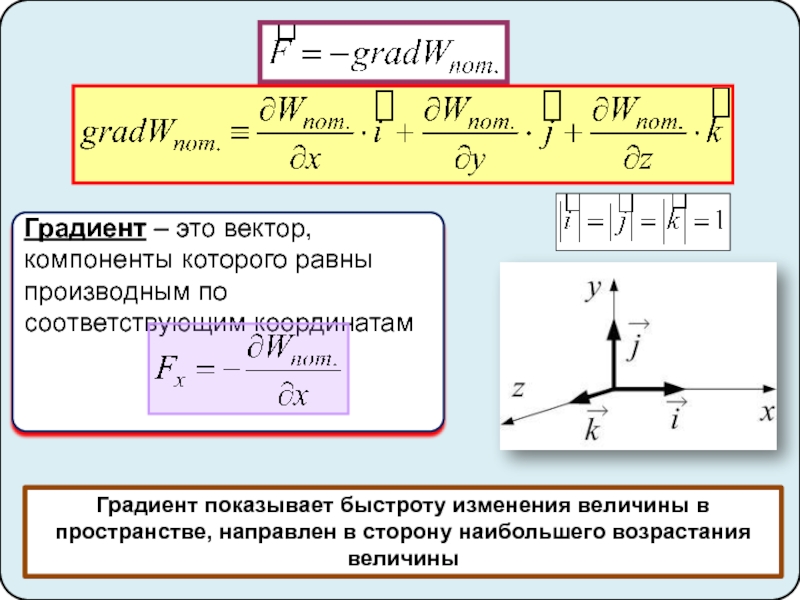
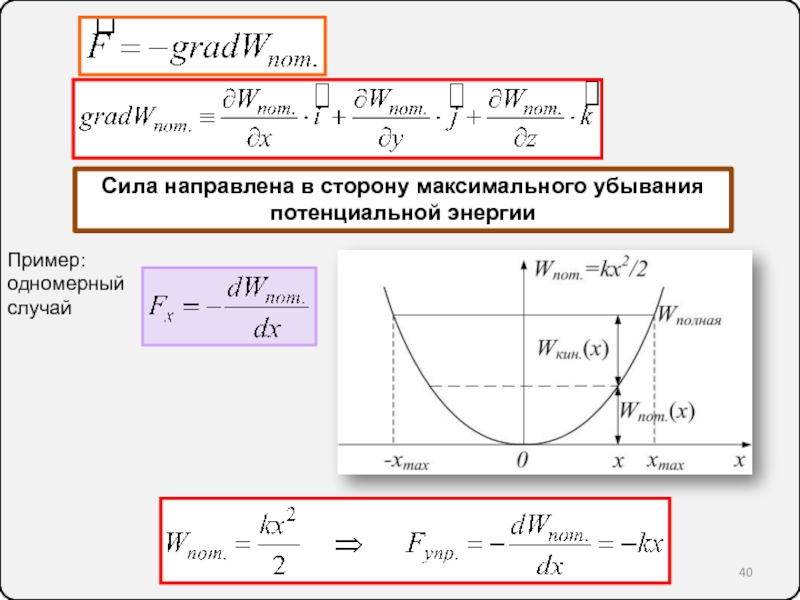
неинерциальные системы отсчёта
3.
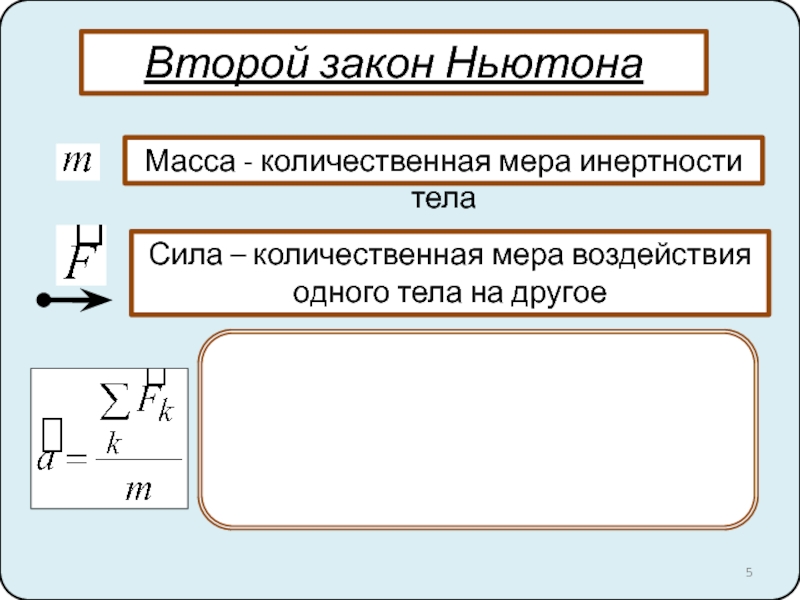
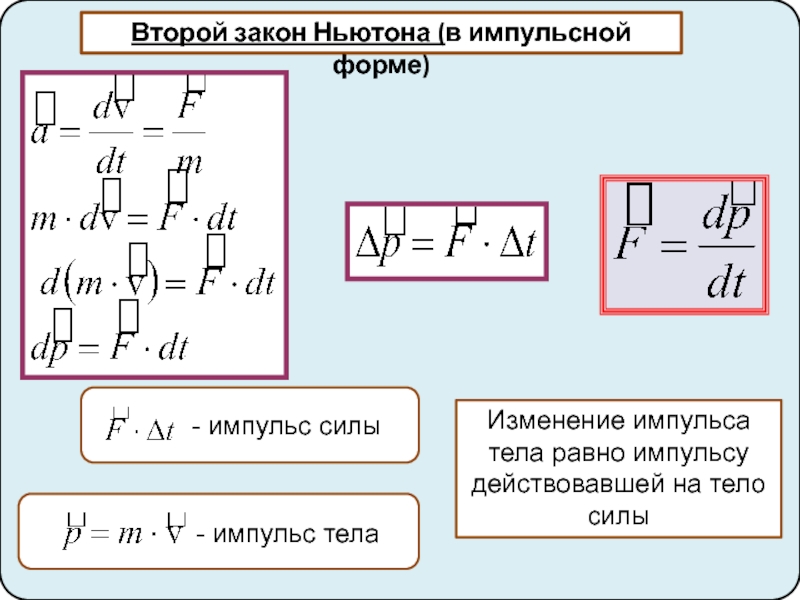
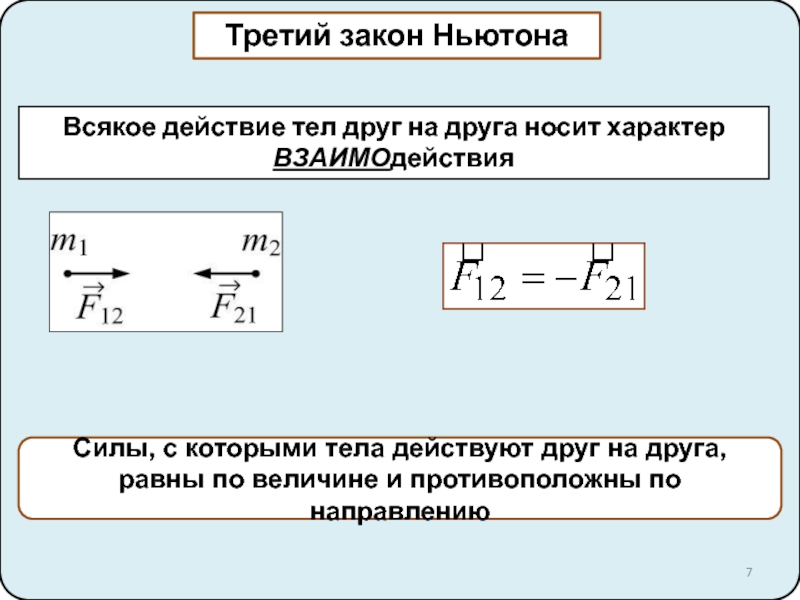
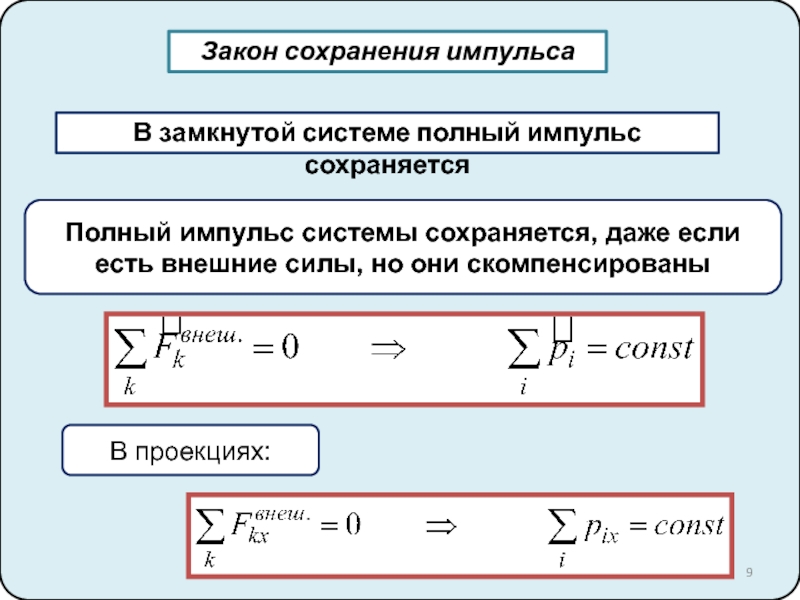
Второй закон Ньютона. Импульс тела 4. Третий закон Ньютона. Закон сохранения импульса
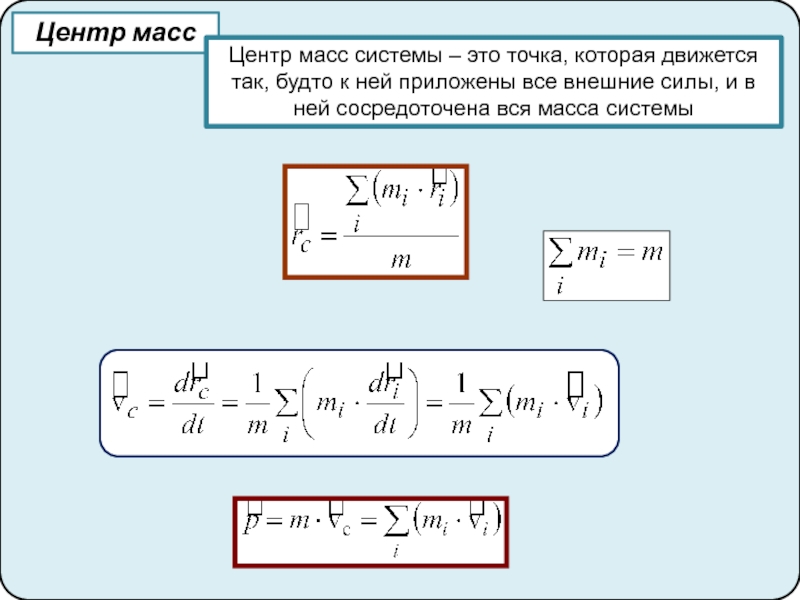
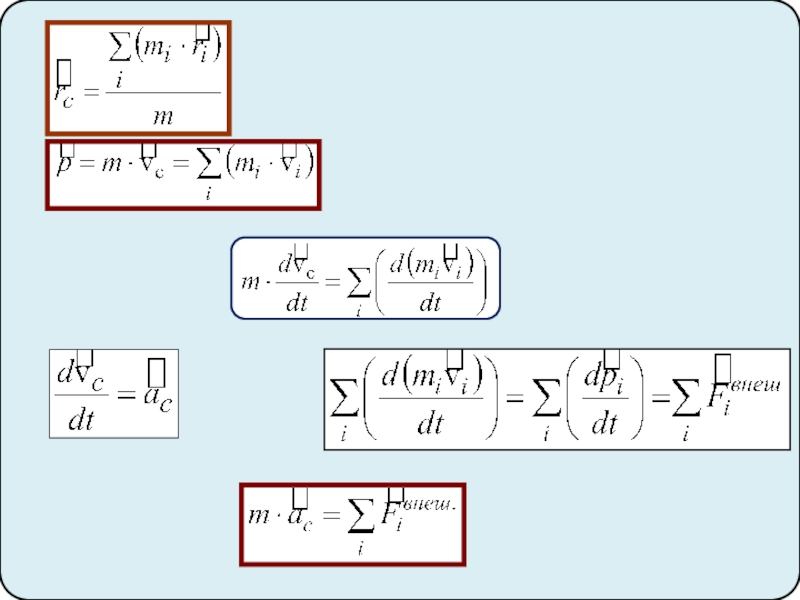
5. Центр масс
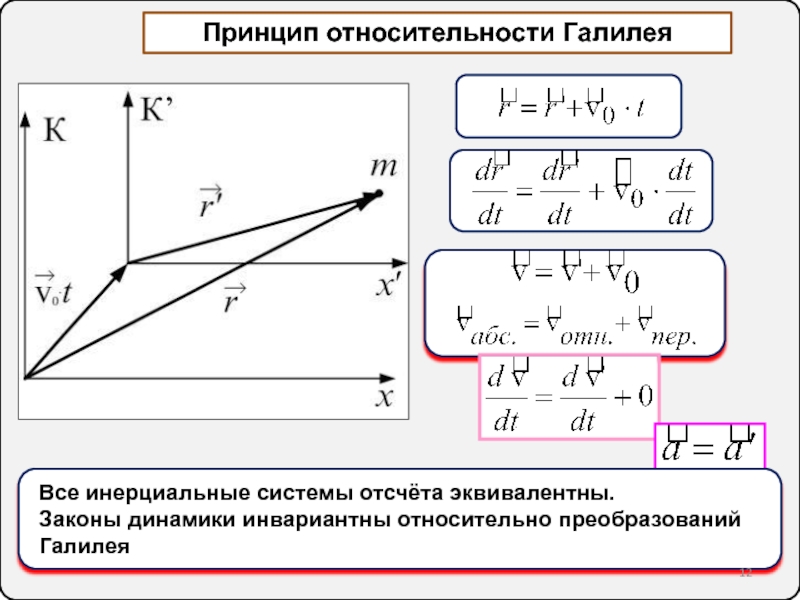
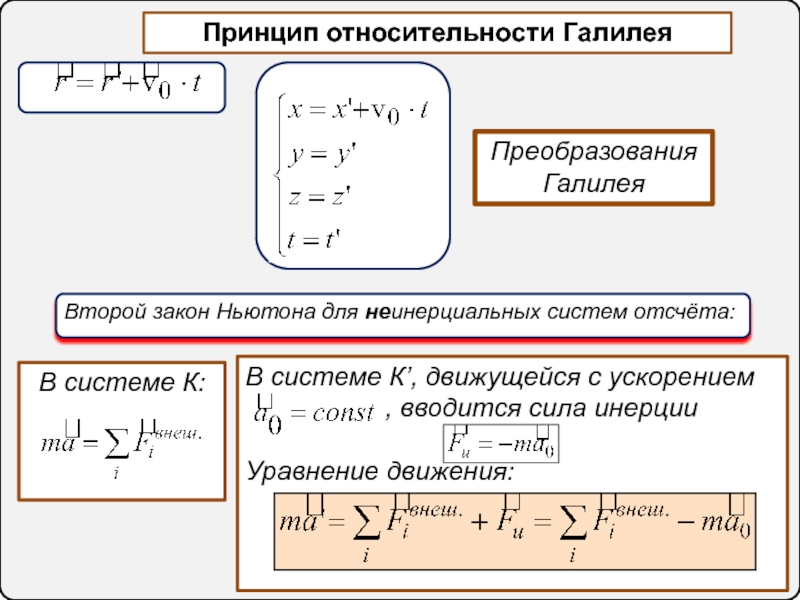
6. Принцип относительности Галилея. Преобразования Галилея. Закон сложения скоростей в классической механике. Второй закон Ньютона для неинерциальных систем отсчёта
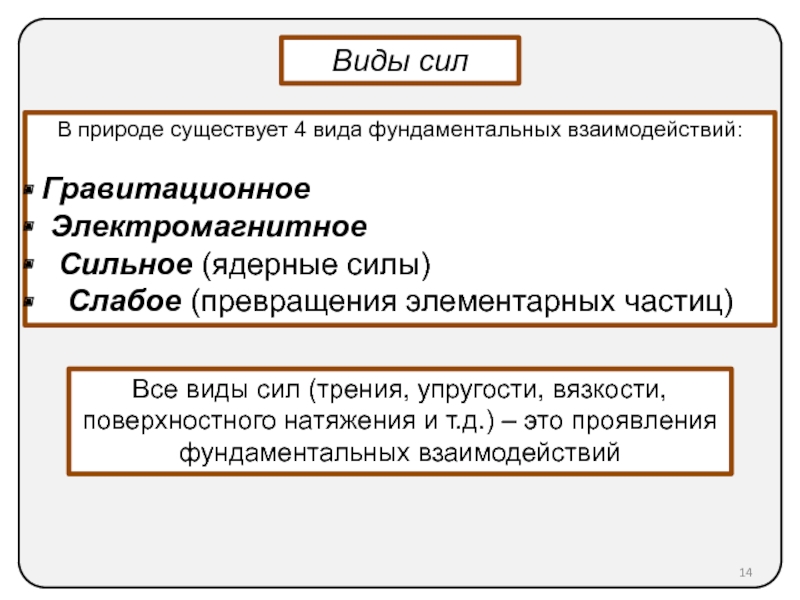
7. Виды сил
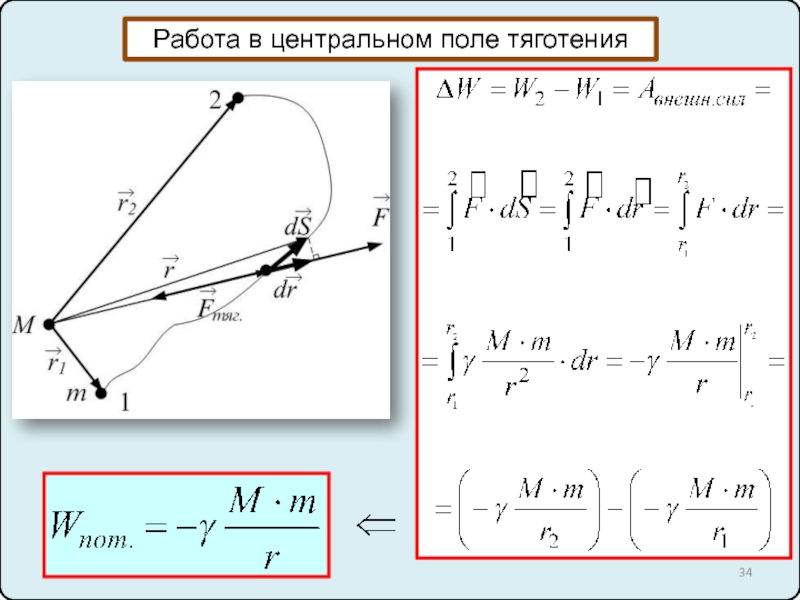
8. Закон всемирного тяготения. Сила тяжести. Вес тела
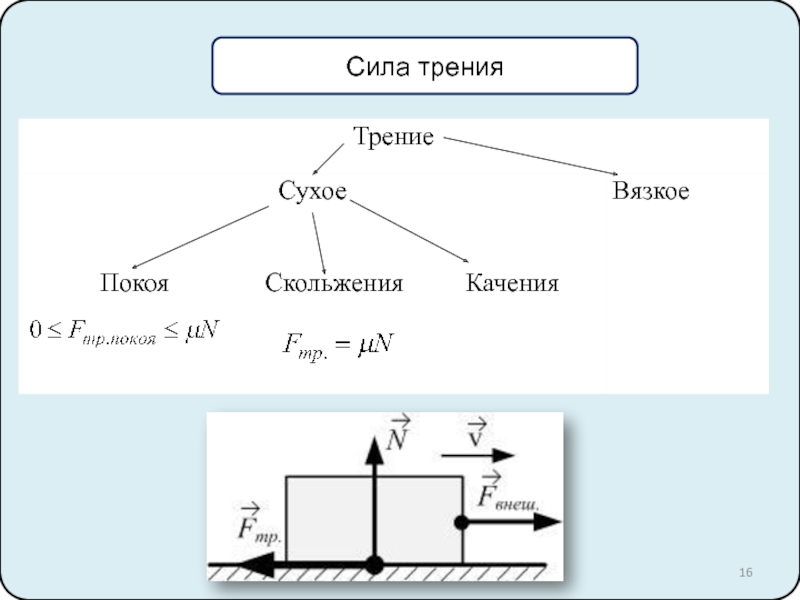
9. Сила трения
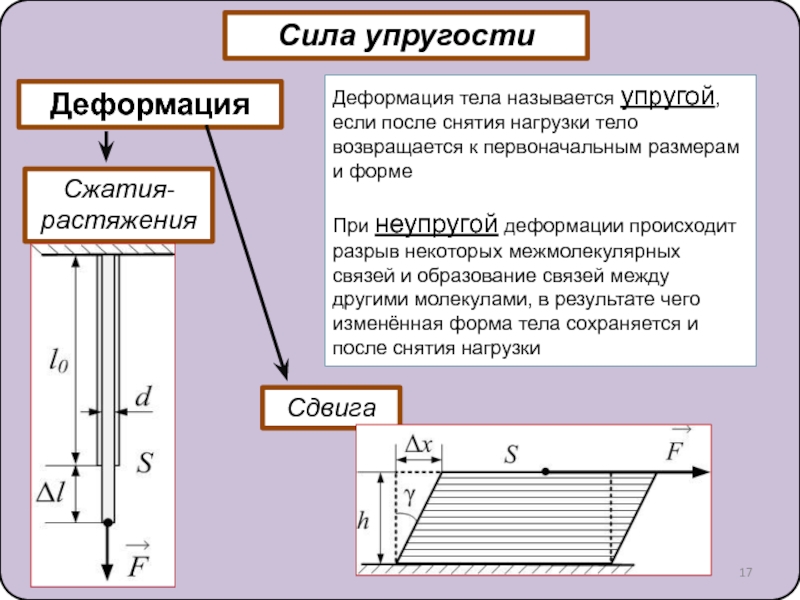
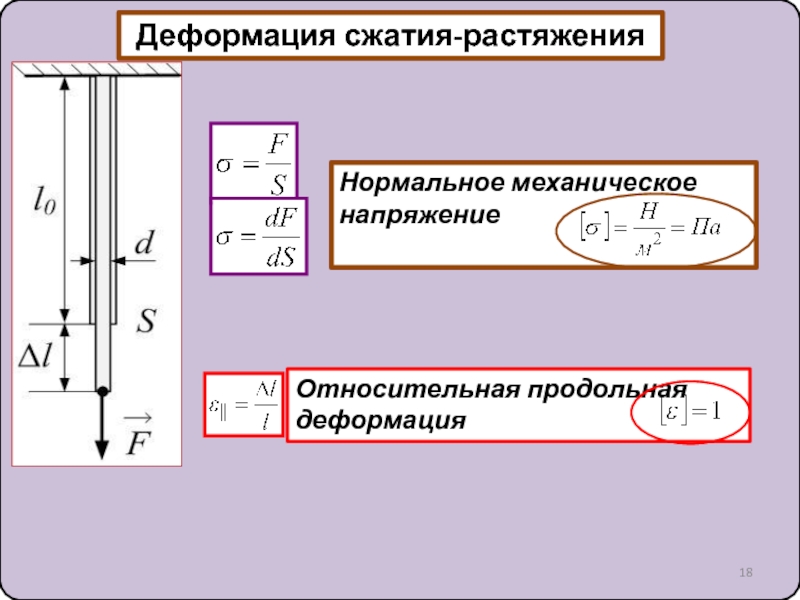
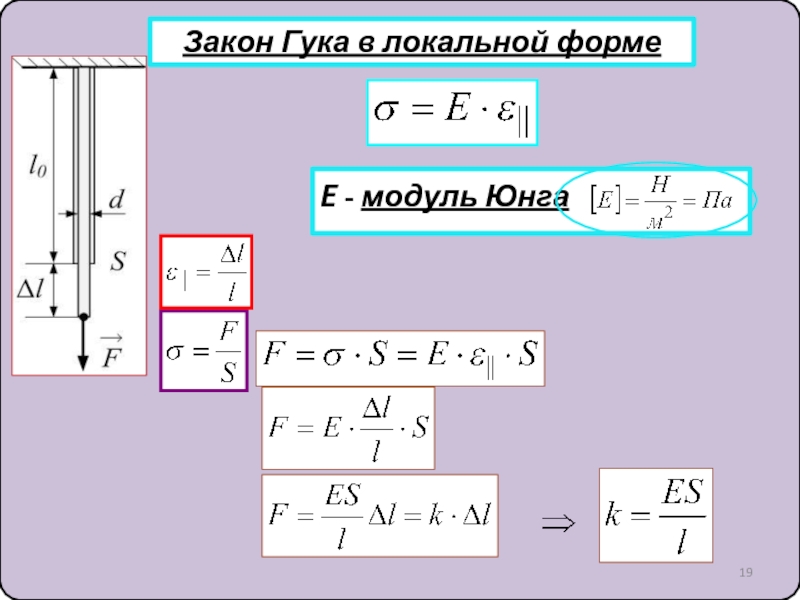
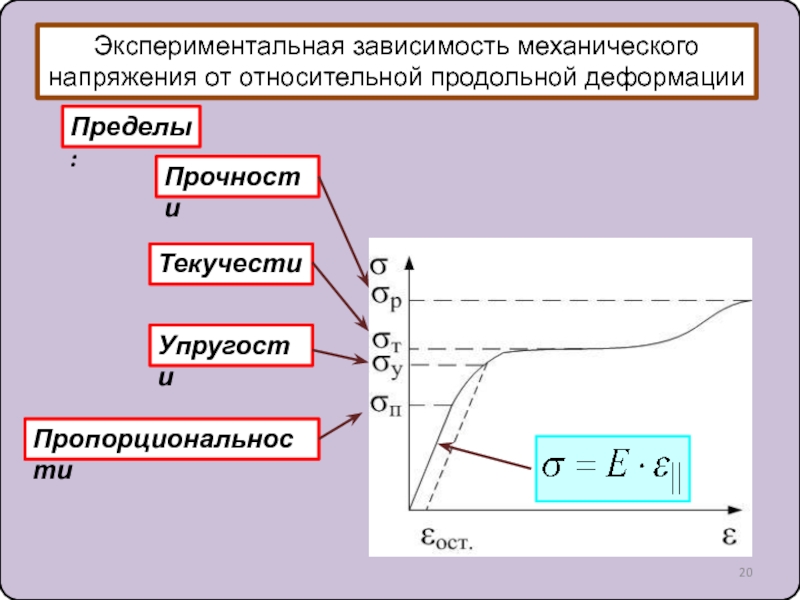
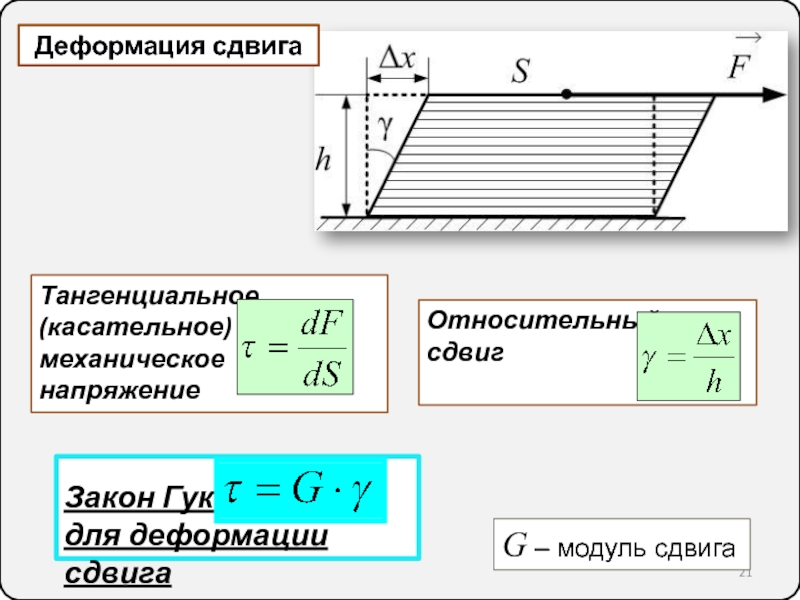
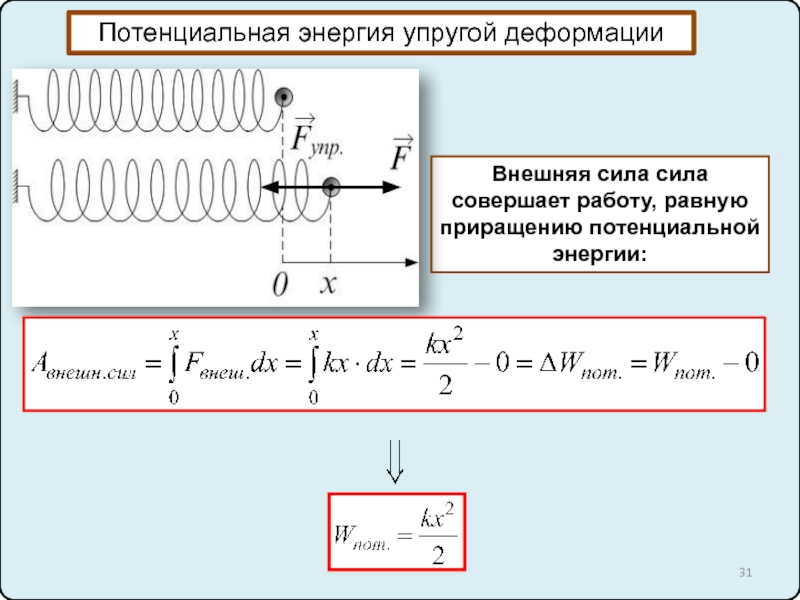
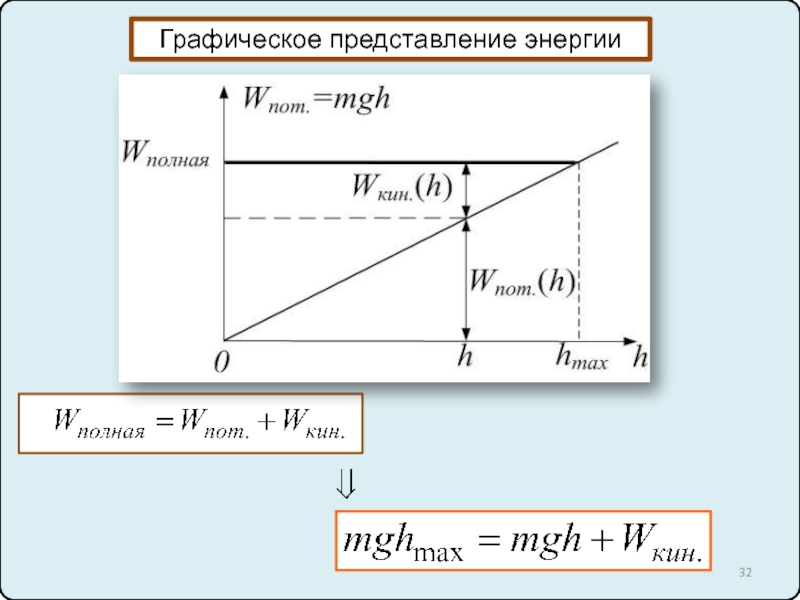
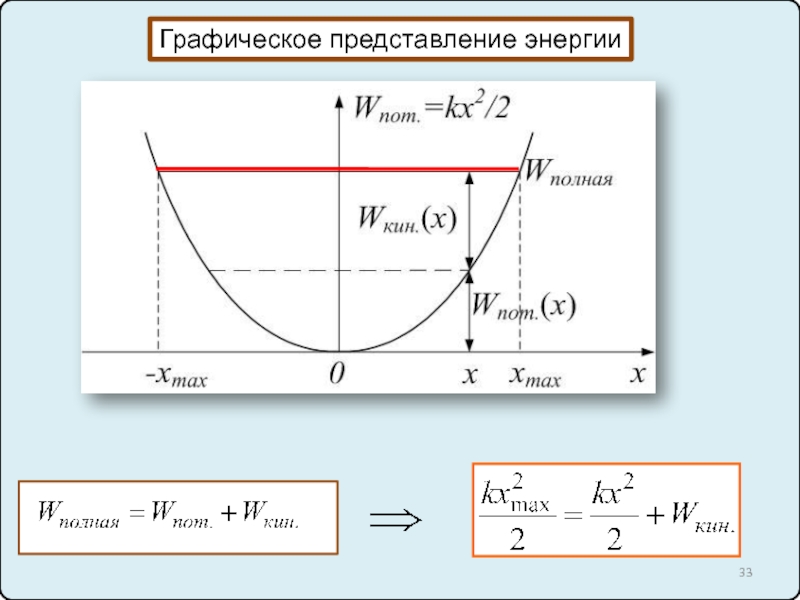
10. Силы упругости