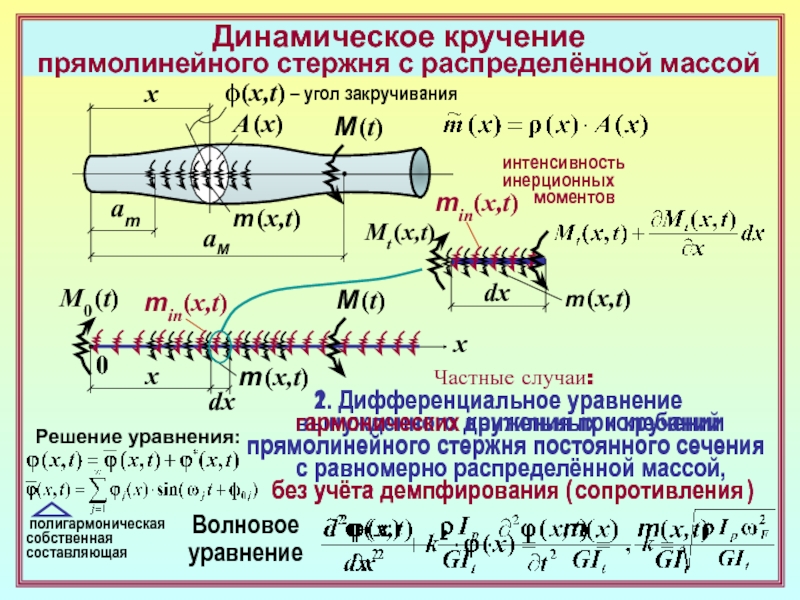
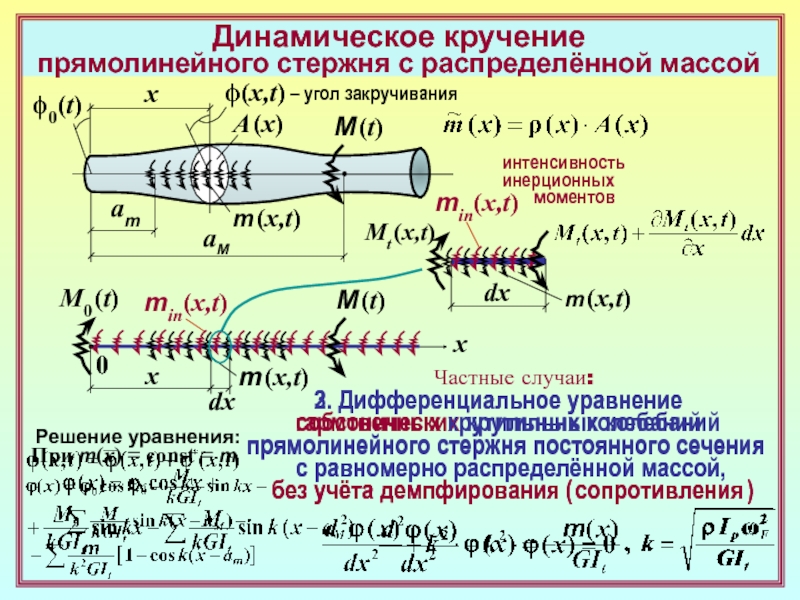
(x,t)
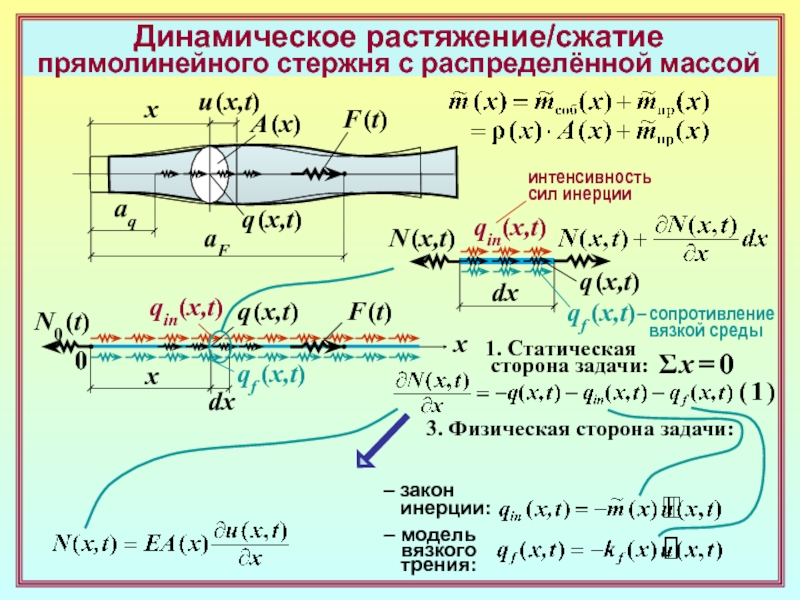
aq
aF
x
x
dx
q (x,t)
F (t)
qin(x,t)
qf (x,t)
0
N0 (t)
dx
N (x,t)
q (x,t)
qin(x,t)
qf (x,t)
интенсивность
сил инерции
– сопротивление
вязкой
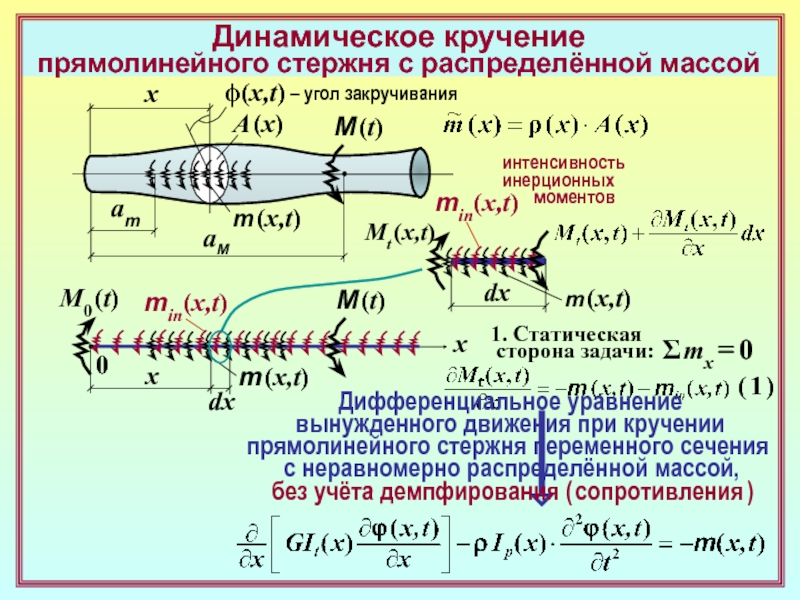
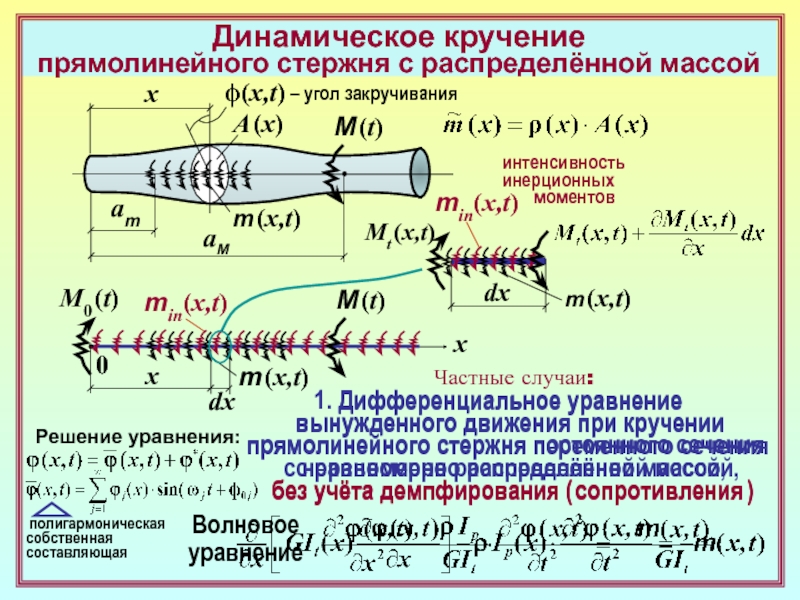
среды1. Статическая
сторона задачи:
Σ x = 0
( 1 )
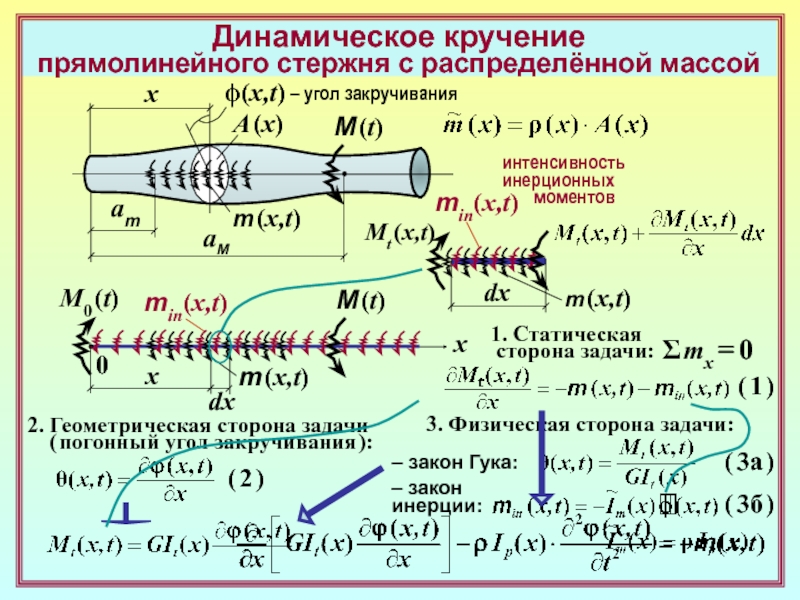
2. Геометрическая сторона задачи
(соотношение Коши):
( 2 )
3. Физическая сторона задачи:
– закон Гука:
( 3а )
– закон
инерции:
( 3б )
– модель
вязкого
трения:
( 3в )