Слайд 1Дисциплина:
«Автоматизированный электрический привод»
Лекция № 3:
УРАВНЕНИЕ ДВИЖЕНИЯ ЭЛЕКТРОПРИВОДА И ЕГО
АНАЛИЗ. ПРИВЕДЕНИЕ МОМЕНТОВ К ОСИ ВРАЩЕНИЯ ВАЛА ЭЛЕКТРОДВИГАТЕЛЯ
Доцент кафедры к.
т. н.
ГОРПИНЧЕНКО Александр Владимирович
СЕВАСТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «ВОЗОБНОВЛЯЕМЫЕ ИСТОЧНИКИ ЭНЕРГИИ И ЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ И СЕТИ»
Слайд 21. Уравнение движения электропривода и его анализ.
2. Приведение статических моментов
к валу электродвигателя.
3. Приведение моментов инерции к валу электродвигателя.
1
ВОПРОСЫ
ЛИТЕРАТУРА
М.Г.Чиликин, А.С.Сандлер
«Общий курс электропривода», стр. 29…31, 38...40.
Слайд 32
Правильный выбор двигателя возможен лишь на основе учета динамических свойств
ЭП.
Динамические свойства ЭП определяют его работу в переходных режимах, т.е.
при переходе от одного установившегося режима работы к другому.
Динамические свойства ЭП зависят от габаритов ЭД и ИМ, вида передаточного звена, электрических параметров двигателя, схемы его включения и ряда других показателей.
Исследование характера движения ЭП в переходных режимах производится на основе решения уравнения движения.
Уравнение движения связывает моменты, действующие в системе ЭП, с изменением скорости вращения.
В большинстве случаев, вращающий момент создается ЭД, а со стороны ИМ действует полезный момент сопротивления.
Полезный момент нагрузки и момент сил трения образуют статический момент сопротивления.
Мс = Мпол+ М0 (1)
Слайд 43
В установившемся режиме, характеризующийся постоянством
скорости электромеханической системы Ω=const,
вращающий момент уравновешивается моментом Мc , а их разность равна
нулю.
М – Мс= 0 (2)
При этом запас кинетической энергии всех вращающихся частей системы также постоянный.
Переходный режим, сопровождающийся изменением скорости Ω, имеет место при неравенстве моментов М >< Мс. При этом избыточный момент уравновешивается динамическим или инерционным моментом.
М – Мс = Мизб = J (3)
М – момент, создаваемый двигателем, [Нм] ;
Мс – статический момент сопротивления, [Нм]
J = mρ2 – момент инерции привода, [кг м2] ;
ρ – радиус инерции, [м].
Ω – угловая скорость вращения ЭД, [1/c] ;
t – время, [c] .
Динамический момент возникает при всяком изменении скорости системы и характеризует изменение запаса её кинетической энергии.
Слайд 54
Момент инерции может быть выражен так:
J = m ∙
ρ2 = ∙ , (4)
где: G –
вес, [Н];
g = 9,81 – ускорение свободного падения, [м/с2];
D – диаметр, [м].
Величина GD2 [Н∙м2] называется маховым моментом. Если выразить J через GD2, а Ω через частоту вращения n [об/мин],
то получим удобное для практических расчетов выражение
M – Mс = (5)
Значения маховых моментов GD2 обычно приводятся в каталогах для ЭД.
Слайд 65
Из анализа уравнения движения видно:
1) при М >
Мс ∙ > 0, т. е. имеет
место ускорение электропривода;
2) при М < Мс ∙ < 0, т. е. имеет место замедление электропривода
(замедление может быть и при отрицательном моменте М – тормозной режим);
3) при М = Мс ∙ = 0, следовательно Ω = const и ЭП работает в установившемся режиме.
При рассмотрении уравнения движения необходимо правильно определить знаки действующих моментов, а именно:
а) моменты, действующие в направлении вращения [+M] и [+Ω ];
б) моменты, действующие встречно направлению вращения [–M] и соответственно [+ Ω].
Момент двигателя: [+M] соответствует двигательному режиму,
[– M] соответствует тормозному режиму.
Статический момент сопротивления: [– Mср ] – реактивный момент,
[±Mсп] – потенциальный момент.
Слайд 76
Учитывая возможные значения знаков моментов, уравнение движения в общем виде
может быть записано
±M Mс = J
. (6)
Примеры анализа уравнения движения.
Исходное положение – неподвижное состояние системы Ω=0
При условии: а) М – Мс = J > 0, Ω возрастёт, что соответствует разгону при подъёме груза (рис. 1а);
б) М – Мс = 0 , Ω = const соответствует установившемуся режиму двигателя при подъёме груза (рис.1а);
в) М – Мс = J < 0 , Ω снижается, что соответствует торможению при подъёме груза (рис. 1а).
Слайд 87
Рисунок 1.
При условии:
а) М + Мс = J
> 0 , Ω возрастает , что соответствует разгону при
спуске груза (рис. 1б) ;
б) –М + Мс = J < 0 , Ω снижается, что соответствует торможению при спуске груза, при этом М > Мс.
Слайд 98
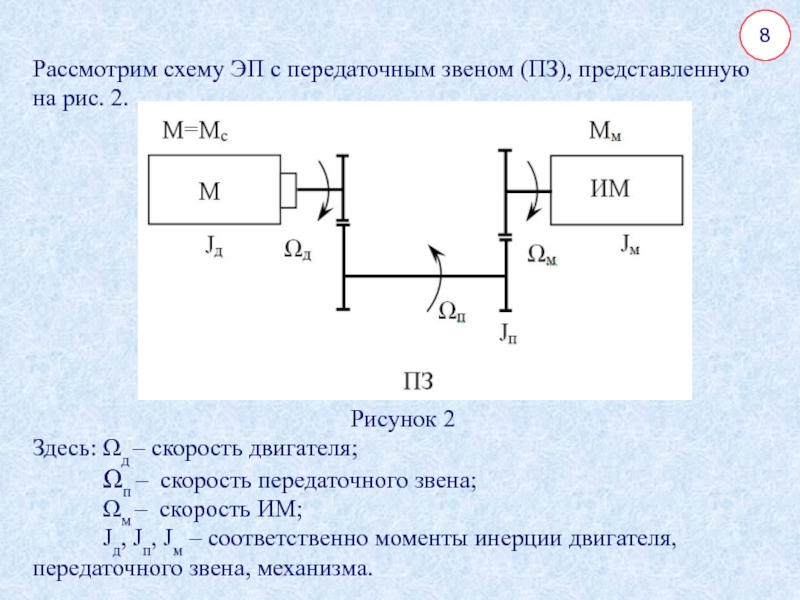
Рассмотрим схему ЭП с передаточным звеном (ПЗ), представленную на рис.
2.
Рисунок 2
Здесь: Ωд – скорость двигателя;
Ωп – скорость передаточного звена;
Ωм
– скорость ИМ;
Jд, Jп, Jм – соответственно моменты инерции двигателя, передаточного звена, механизма.
Слайд 109
Из уравнения баланса мощностей имеем:
(7)
где: Р – мощность двигателя;
Рм – мощность ИМ;
η пер – КПД передачи.
(8)
Из (8) получаем выражение для приведения статических моментов к валу ЭД:
, (9)
где: .
Слайд 1110
В общем случае передаточное звено может иметь сложную структуру и
передаточное число k = k1∙ k2∙ k3∙…∙ kn,
где ki –
передаточное число единичной пары или единичного звена.
Аналогично: ηпер = η1 ∙ η2 ∙ η3 ∙... ∙ηn, где ηi – К.П.Д. единичной пары.
Тогда окончательное выражение для приведения к валу ЭД статических моментов запишется:
(10)
Слайд 1211
Приведённым моментом инерции называется момент инерции некоторой эквивалентной простейшей системы
(рис. 3), все элементы которой вращаются со скоростью ΩД и
обладают запасом кинетической энергии равным запасу исходной системы (рис.2).
Рисунок 3
(11)
Слайд 1312
Две системы – простейшая (рис. 3) и исходная (рис. 2)
во всех динамических режимах будут абсолютно идентичны, однако, простейшая система
удобнее для анализа. Найдём выражение для приведённого момента из выражения (11).
(12)
Здесь
Тогда
КПД обычно при определении Jпр не учитывают..