Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисциплина Численные методы
Содержание
- 1. Дисциплина Численные методы
- 2. Преподаватель Дмитрий Игоревич Балашов
- 3. Дисциплина состоит из 6 модулей:Численное решение нелинейных
- 4. Численное решение нелинейных уравнений
- 5. Общий вид нелинейного уравненияf(x)=0 где x – аргумент, f(x) – функционал одной переменной
- 6. Существуют различные методы решения нелинейных уравнений Наиболее распространенный: аналитический метод
- 7. Трансцендентные уравненияПример: Или после преобразования:
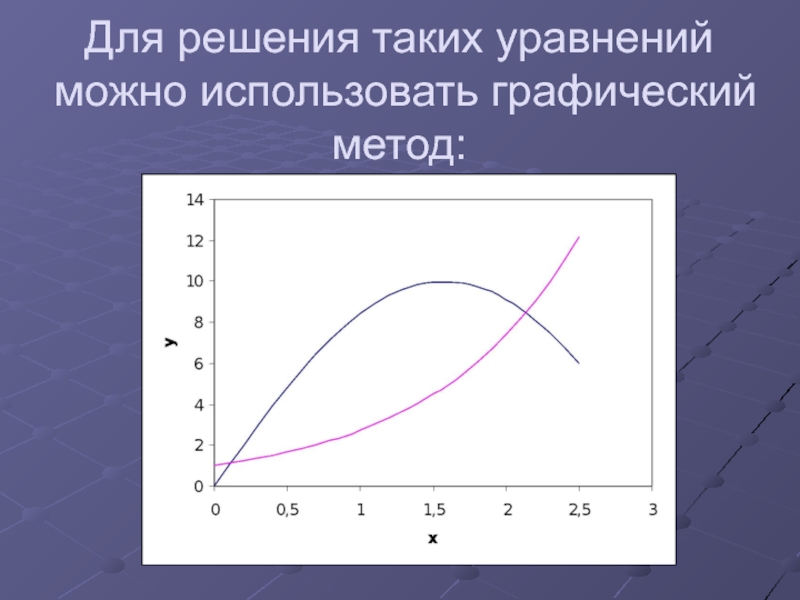
- 8. Для решения таких уравнений можно использовать графический метод:
- 9. Недостаток графического метода:Низкая точность получаемого результата.Также для решения подобного рода уравнений можно использовать численные методы
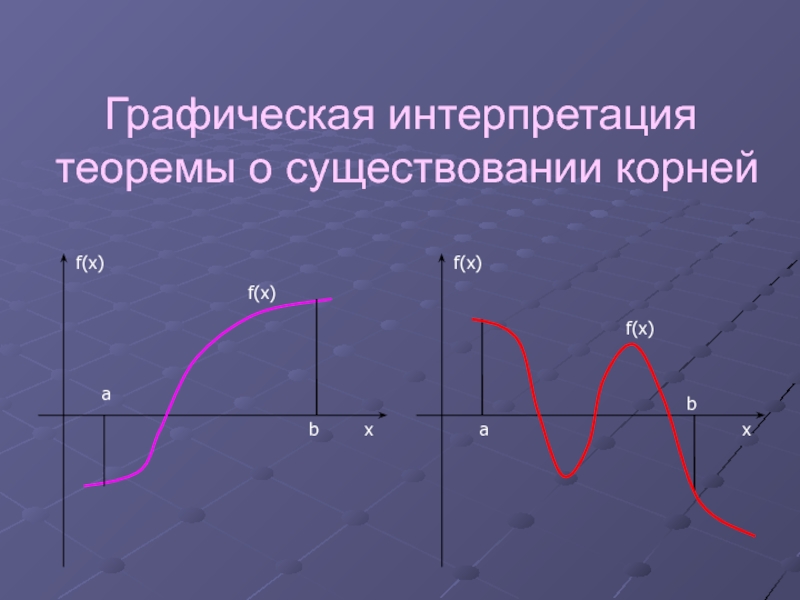
- 10. Теоремао существовании корней уравнения f(x)=0Если на концах
- 11. Графическая интерпретация теоремы о существовании корней
- 12. Обратная теорема не верна
- 13. Большинство численных методов основаны на этой теоремеВ
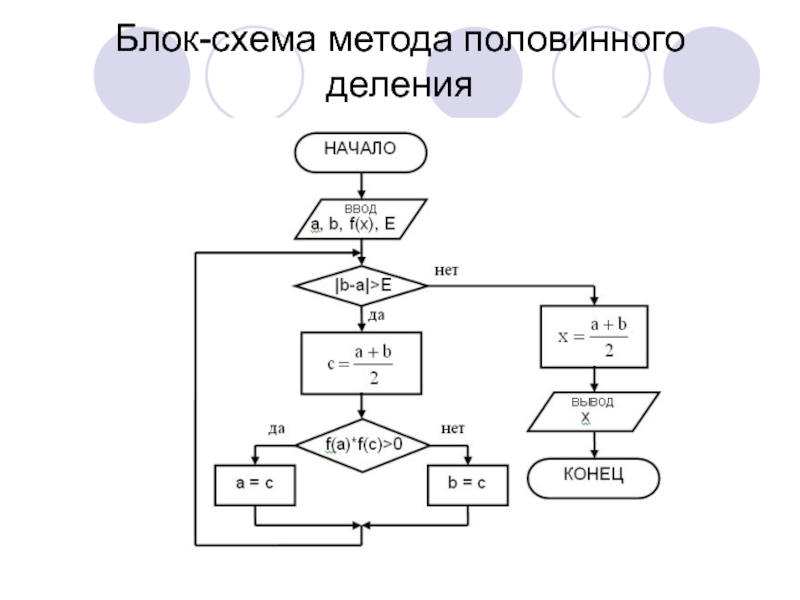
- 14. Метод половинного деления (метод дихотомии, метод бисекции)Исходные данные для реализации метода:f(x)=0[a, b]E
- 15. Алгоритм метода:Отрезок ab делится пополам точкой с.Рассчитываются
- 16. Графическая интерпретация метода:
- 17. Блок-схема метода половинного деления
- 18. ДОСТОИНСТВА методаПростота методаУстойчивость методаНЕДОСТАТОК методаНизкая скорость сходимости
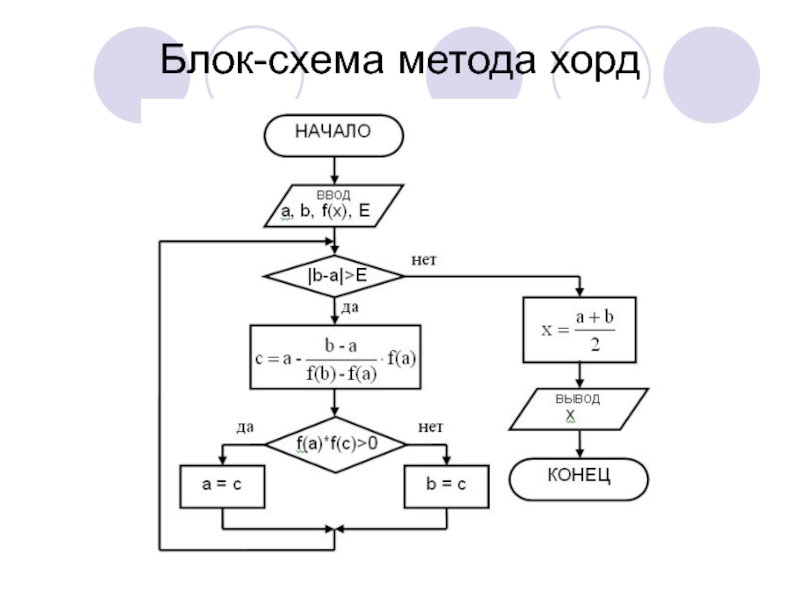
- 19. Метод хорд Исходные данные для реализации метода:f(x)=0[a, b]E
- 20. Алгоритм метода:Отрезок ab делится на 2 отрезка
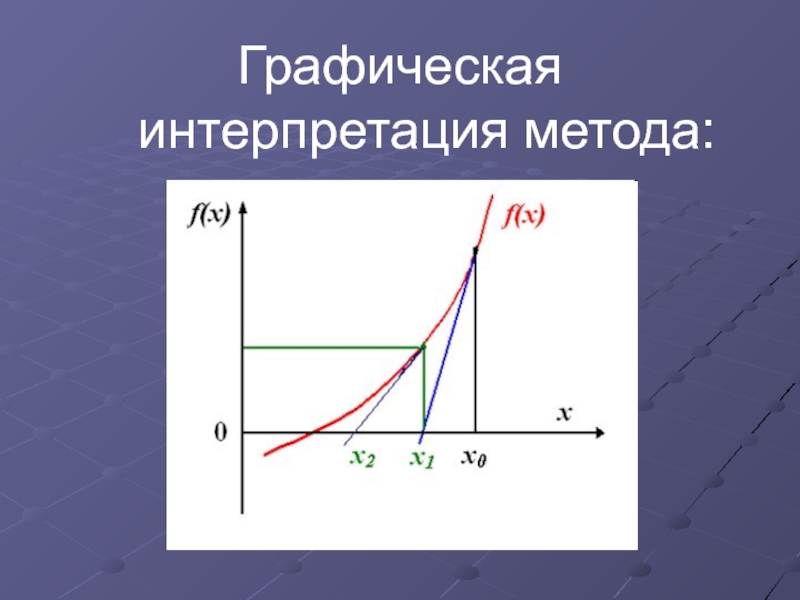
- 21. Графическая интерпретация метода:
- 22. Блок-схема метода хорд
- 23. ДОСТОИНСТВА методаПростота методаУстойчивость методаБолее высокая скорость сходимостиНЕДОСТАТОК методаДля некоторых частных случаев метод не применим
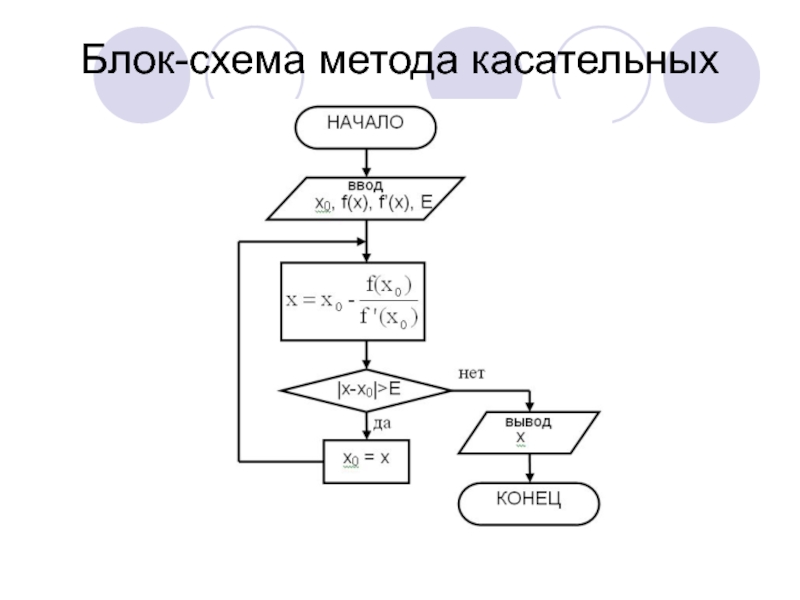
- 24. Метод касательных (метод Ньютона)Исходные данные для реализации метода:f(x)=0f ’(x)x0E
- 25. Алгоритм метода:В точке x0 к графику функции
- 26. Графическая интерпретация метода:
- 27. Блок-схема метода касательных
- 28. ДОСТОИНСТВО методаВысокая скорость сходимостиНЕДОСТАТКИ методаНеобходимость задавать производную функции в аналитическом видеМетод является неустойчивым
- 29. Метод секущих Метод секущих является модификацией метода касательныхИсходные данные для реализации метода:f(x)x0E
- 30. Алгоритм метода:Алгоритм аналогичен предыдущему методу, но производная
- 31. ДОСТОИНСТВА методаВысокая скорость сходимостиНет необходимости задавать производную функции в аналитическом видеНЕДОСТАТОК методаМетод является неустойчивым
- 32. Скачать презентанцию
Преподаватель Дмитрий Игоревич Балашов
Слайды и текст этой презентации
Слайд 3Дисциплина состоит из 6 модулей:
Численное решение нелинейных уравнений.
Численное решение СЛАУ.
Численное
решение СНУ.
ЗАЧЕТСлайд 6Существуют различные методы решения нелинейных уравнений
Наиболее распространенный:
аналитический метод
Слайд 9Недостаток графического метода:
Низкая точность получаемого результата.
Также для решения подобного рода
уравнений можно использовать численные методы
Слайд 10Теорема
о существовании корней уравнения f(x)=0
Если на концах интервала [a, b]
функция f(x) имеет разные знаки, то это значит, что в
интервале [a, b] уравнение f(x)=0 имеет хотя бы один корень.Слайд 13Большинство численных методов основаны на этой теореме
В дальнейшем примем допущение
о том, что на интервале [a, b] имеется только один
корень уравнения f(x)=0Слайд 14Метод половинного деления
(метод дихотомии,
метод бисекции)
Исходные данные для реализации метода:
f(x)=0
[a, b]
E
Слайд 15Алгоритм метода:
Отрезок ab делится пополам точкой с.
Рассчитываются значения функции f(x)
в точках a, b и c.
Один из отрезков ac или
cb, на концах которого функция f(x) имеет одинаковые знаки, отбрасывают и далее продолжают работать с оставшимся отрезком.Процесс повторяется до тех пор, пока длина оставшегося отрезка не станет меньше величины точности Е.
|a-b|
В этом случае за корень уравнения можно принять середину полученного отрезка
x=(a+b)/2
Слайд 18ДОСТОИНСТВА метода
Простота метода
Устойчивость метода
НЕДОСТАТОК метода
Низкая скорость сходимости
Слайд 20Алгоритм метода:
Отрезок ab делится на 2 отрезка точкой с. Точка
с является точкой пересечения оси абсцисс ОХ с хордой, соединяющей
точки f(a) и f(b).Рассчитываются значения функции f(x) в точках a, b и c.
Один из отрезков ac или cb, на концах которого функция f(x) имеет одинаковые знаки, отбрасывается и далее продолжают работать с оставшимся отрезком.
Процесс повторяется до тех пор, пока длина оставшегося отрезка не станет меньше величины точности Е.
|a-b|
x=(a+b)/2
Слайд 23ДОСТОИНСТВА метода
Простота метода
Устойчивость метода
Более высокая скорость сходимости
НЕДОСТАТОК метода
Для некоторых частных
случаев метод не применим
Слайд 25Алгоритм метода:
В точке x0 к графику функции f(x) проводится касательная.
Находится более точное значение x – это точка пересечения касательной
с осью абсцисс ОХ.Таким образом каждая последующая точка будет лежать ближе к истинному решению, чем предыдущая.
Последующая точка рассчитывается через предыдущую по формуле
xi+1=xi-f(xi)/f ’(xi)
Процесс повторяется до тех пор, пока разность между последующей и предыдущей точкой не станет меньше величины точности Е
|xi+1-xi|
В этом случае за корень уравнения можно принять последнюю найденную точку xi.








![Дисциплина Численные методы Теоремао существовании корней уравнения f(x)=0Если на концах интервала [a, b] функция Теоремао существовании корней уравнения f(x)=0Если на концах интервала [a, b] функция f(x) имеет разные знаки, то это](/img/thumbs/5dafad8abeba22d1d7e8cb1745c2467a-800x.jpg)

![Дисциплина Численные методы Большинство численных методов основаны на этой теоремеВ дальнейшем примем допущение о Большинство численных методов основаны на этой теоремеВ дальнейшем примем допущение о том, что на интервале [a, b]](/img/thumbs/7396e44a43d742fc3534e5f86c553000-800x.jpg)
![Дисциплина Численные методы Метод половинного деления (метод дихотомии, метод бисекции)Исходные данные для реализации метода:f(x)=0[a, b]E Метод половинного деления (метод дихотомии, метод бисекции)Исходные данные для реализации метода:f(x)=0[a, b]E](/img/thumbs/ec0657c15e683b4b4a2acbc22f546842-800x.jpg)



![Дисциплина Численные методы Метод хорд Исходные данные для реализации метода:f(x)=0[a, b]E Метод хорд Исходные данные для реализации метода:f(x)=0[a, b]E](/img/thumbs/04d59909ffbd93d72752250d4b4364ed-800x.jpg)