Слайд 1Дополнительные возможности анализа данных в MS Excel
Слайд 21. Аппроксимация экспериментальных данных. Линии тренда
Слайд 3На практике часто приходится сталкиваться с задачей о сглаживании экспериментальной
зависимости или задачей аппроксимации.
Аппроксимация (от лат. Approximo - приближение) -
замена одних математических объектов (например, чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (напр., кривых линий близкими к ним ломаными).
Аппроксимация - приближенное решение сложной функции с помощью более простых, резко ускоряет и упрощает решение задач. В экономике целью аппроксимации часто является укрупнение характеристик моделируемых экономических объектов.
Слайд 4Аппроксимацией называется процесс подбора эмпирической формулы для установленной из опыта
функциональной зависимости у = f (x). Эмпирические формулы служат для
аналитического представления экспериментальных данных.
В простейшем случае задача аппроксимации экспериментальных данных выглядит следующим образом.
Пусть какие-то данные, полученные практическим путем (в ходе эксперимента или наблюдения), можно представить парами чисел (х, у). Зависимость между ними отражает таблица 2.
Таблица 2 - Зависимость экспериментальных X и Y
Слайд 5На основе этих данных нужно подобрать функцию y = f
(x), которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными
и по возможности точно отражала общую тенденцию зависимости между х и у, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения в каком-то значении были бы минимальными.
Выяснить вид функции можно либо из теоретических соображений, или анализируя расположение точек (х n; уn) на координатной плоскости.
Например, пусть точки расположены так:
Слайд 6Учитывая то, что практические данные получены с некоторой погрешностью, обусловленной
неточностью измерений, необходимостью округления результатов и т. п., естественно предположить,
что здесь имеет место линейная зависимость у = ах + b.
Чтобы функция приняла конкретный вид, необходимо каким-то образом вычислить а и b.
Слайд 7Расположение экспериментальных точек может иметь самый разный вид, и каждому
соответствует конкретный тип функции.
Построение эмпирической функции сводится к вычислению параметров,
входящих в нее, так чтобы из всех функций такого вида выбрать ту, которая лучше других описывает зависимость между величинами, которые изучаются. То есть сумма квадратов разницы между табличными значениями функции в некоторых точках и значениями, вычисленными по полученной формуле, должна быть минимальной.
В MS Excel аппроксимация экспериментальных данных осуществляется путем построения их графика (х - абстрактные величины) или точечного графика (х - имеет конкретные значения) с последующим подбором соответствующей аппроксимирующей функции (линии тренда).
Слайд 8Возможны следующие варианты функций:
Линейная - у = ах + b.
Обычно применяется в простейших случаях, когда экспериментальные данные растут или
убывают с постоянной скоростью.
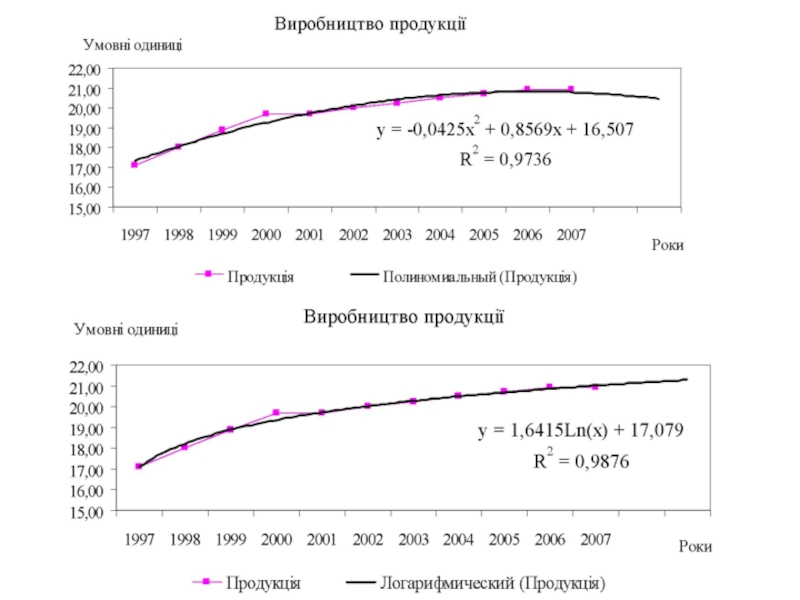
Полиномиальная — у=а0 + a1x2+a2х2 +... + аnхn, где полиномы до шестого порядка включительно (n <= 6), ai — константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов или минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени - не более трех экстремумов и т. .
Логарифмическая - у = alnx + b, где а и b - константы, ln - функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые сначала быстро растут или убывают, а затем постепенно стабилизируются.
Слайд 9Степенная — у = bxa, де а і b —
константы. Аппроксимация степенной функцией используется для экспериментальных данных, со скоростью
роста, которая постоянно увеличивается (или убывает). Данные не должны иметь нулевых или отрицательных значений.
Экспоненциальная — у= beax, где а и b — константы, е — основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование следует из теоретических соображений.
Степень близости аппроксимации экспериментальных данных выбранной функции оценивается коэффициентом детерминации (R2). Таким образом, если есть несколько подходящих вариантов типов аппроксимирующих функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1).
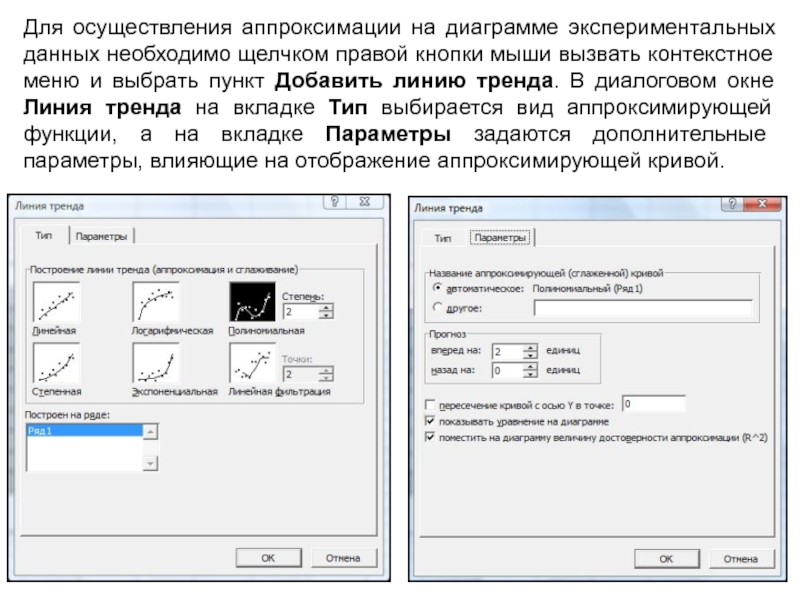
Слайд 10Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой
кнопки мыши вызвать контекстное меню и выбрать пункт Добавить линию
тренда. В диалоговом окне Линия тренда на вкладке Тип выбирается вид аппроксимирующей функции, а на вкладке Параметры задаются дополнительные параметры, влияющие на отображение аппроксимирующей кривой.
Слайд 122. Поиск решения задач линейного программирования (ЗЛП)
Слайд 13Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства,
ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Теорию и методы решения задачи оптимизации изучает математическое программирование.
Математическое
программирование - это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.
В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной.
Теория ЗЛП
Слайд 14Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:
допустимое множество;
целевую
функцию;
критерий поиска (max или min).
Задачи оптимизации, в которых целевая функция и ограничения являются
линейными функциями, разрешаются так называемыми методами линейного программирования.
Слайд 15Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась
ещё в XIX веке.
В 1939 году Л. В. Канторович опубликовал работу «Математические методы организации
и планирования производства», таким образом были заложены основы линейного программирования.
Изучение подобных задач привело к созданию новой научной дисциплины линейного программирования и открыло новый этап в развитии экономико-математических методов.
Термин «программирование» нужно понимать в смысле «планирования» (один из переводов англ. programming). Он был предложен в середине 1940-х годов Д. Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.
Краткая история вопроса
Слайд 16.
Математические модели линейного программирования строятся на основе содержательной постановки экономической
задачи.
Пример.
Типичная задача распределения ресурсов ставится следующим образом.
Пусть фирма выпускает продукцию
четырех типов Продукт1, Продукт2, Продукт3, Продукт4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы.
Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода.
Исходные данные.
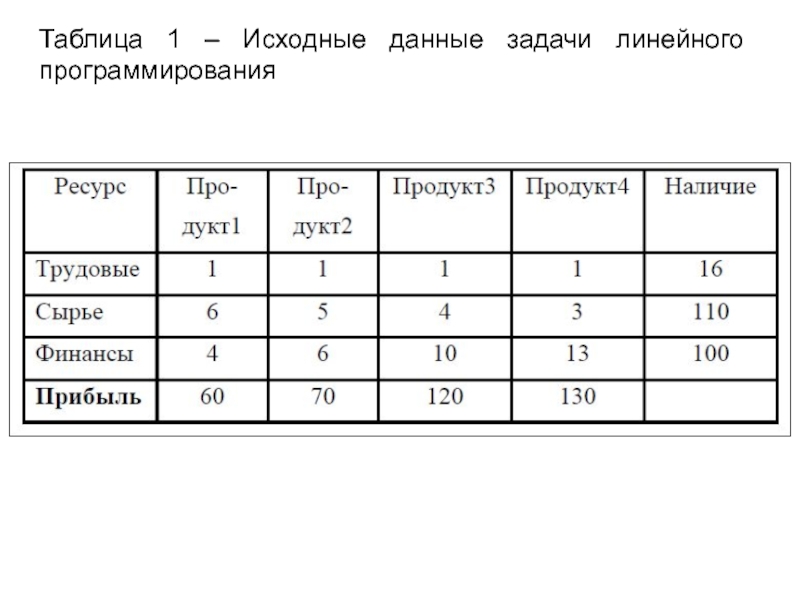
Норма расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 1, там же приведен объем ресурса, которым можно располагать. Требуется определить, в каком количестве надо выпускать продукцию каждого типа, чтобы суммарная прибыль была максимальной.
1 часть - Построение математических моделей линейного программирования
Практика решения ЗЛП
Слайд 17Таблица 1 – Исходные данные задачи линейного программирования
Слайд 18Составление математической модели начинают с выбора переменных задачи. В большинстве
случаев (для ресурсных задач в частности) переменные – неизвестные количества.
После
выбора переменных, исходя из содержательной формулировки задачи, последовательно составляют линейные ограничения, которые эти переменные должны удовлетворять.
При этом нужно следить, чтобы в модель были введены все ограничительные условия и в то же время не было ни одной лишней или записанной в более жесткой форме, чем требуется по условиям задачи.
Следующим шагом является составление целевой функции, которая в математической форме отражает заданный в условиях задачи критерий оптимизации и должна быть линейной.
Заметим, что в некоторых моделях удобнее целевую функцию строить сразу после выбора переменных задачи, т.е. порядок построения модели не является жестким и может изменяться.
После построения модель, если это возможно, упрощают.
Слайд 19Составим математическую модель, для чего введем следующие обозначения:
xj- количество выпускаемой
продукции j-го типа j=1,2,3,4;
bi- количество располагаемого ресурса i-го вида i=1,2,3;
aij-
норма расхода i-го ресурса для выпуска единицы продукции j-го типа;
cj- прибыль, получаемая от реализации единицы продукции j-го типа.
Слайд 20Из таблицы 1 видно, что для выпуска единицы Продукта1 требуется
6 единиц сырья, значит, для выпуска всей продукции первого типа
требуется 6x1 единиц сырья, где x1- количество выпускаемой продукции Продукт1. С учетом того, что для других видов продукции зависимости будут аналогичны, ограничение по сырью будет иметь вид:
6⋅x1+5⋅x2+4⋅x3+3⋅x4 ≤ 110.
В этом ограничении левая часть равна величине требуемого ресурса, а правая показывает количество имеющегося ресурса.
Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции.
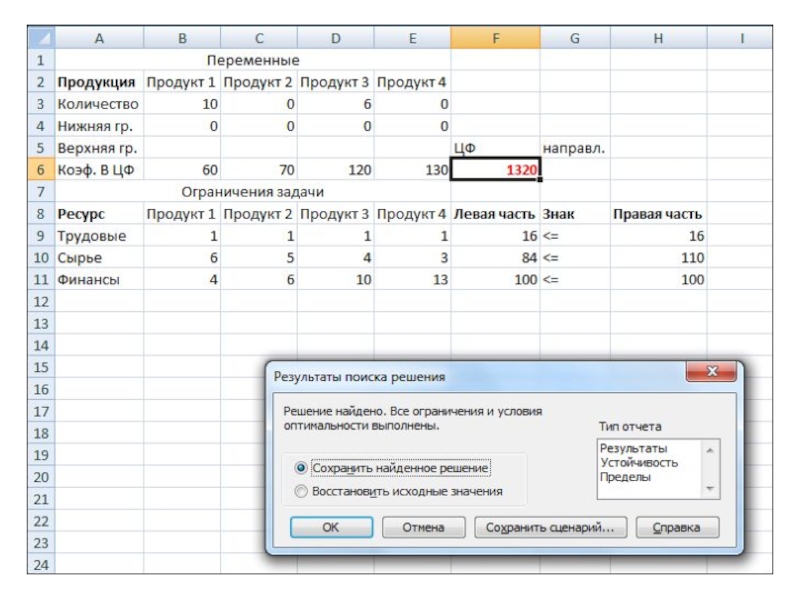
Слайд 21Математическая модель задачи выглядит следующим образом.
Целевая функция имеет вид:
60⋅x1+70⋅x2+120⋅x3+130⋅x4→max
Ограничения имеют
вид:
x1+x2+x3+x4≤16
6⋅x1+5⋅x2+4⋅x3+3⋅x4≤110
4⋅x1+6⋅x2+10⋅x3+13⋅x4≤100
xj≥0; j=1,4 .
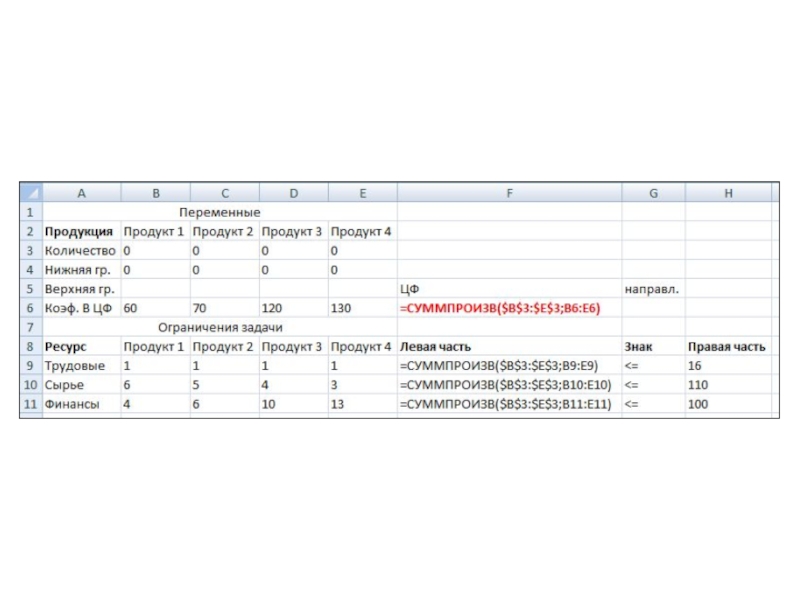
Слайд 22Ввод условий задачи состоит из следующих основных шагов:
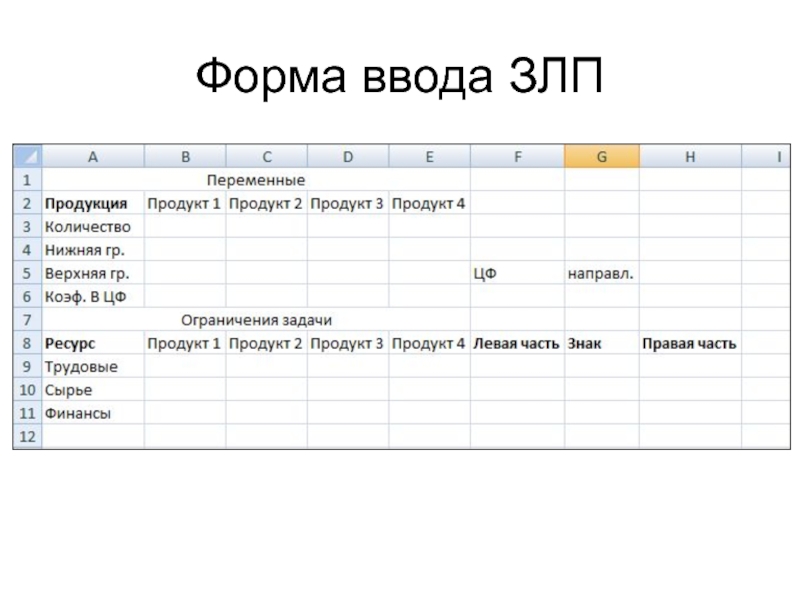
1) Создание формы
для ввода условий задачи.
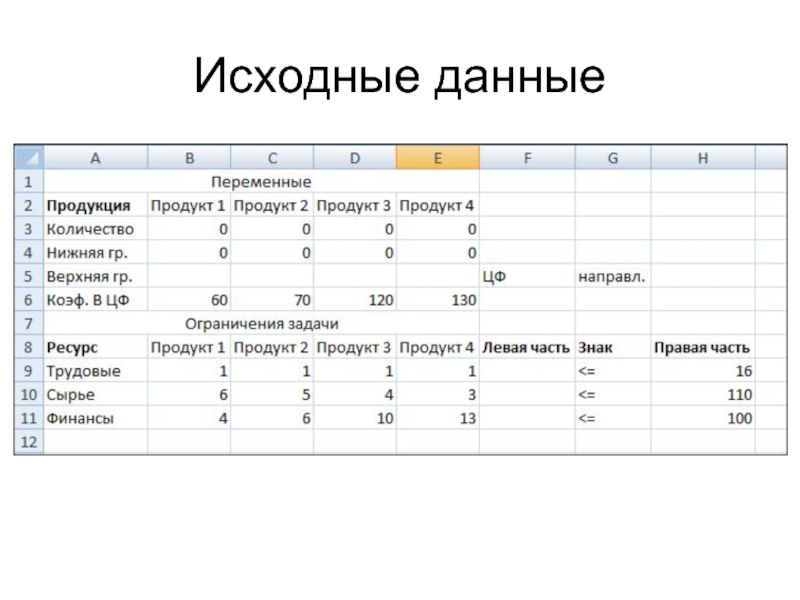
2) Ввод исходных данных (коэффициентов математической модели).
3)
Ввод целевой функции, ограничений и граничных условий.
2 часть – Решение задачи линейного программирования с помощью табличного процессор MS Excel
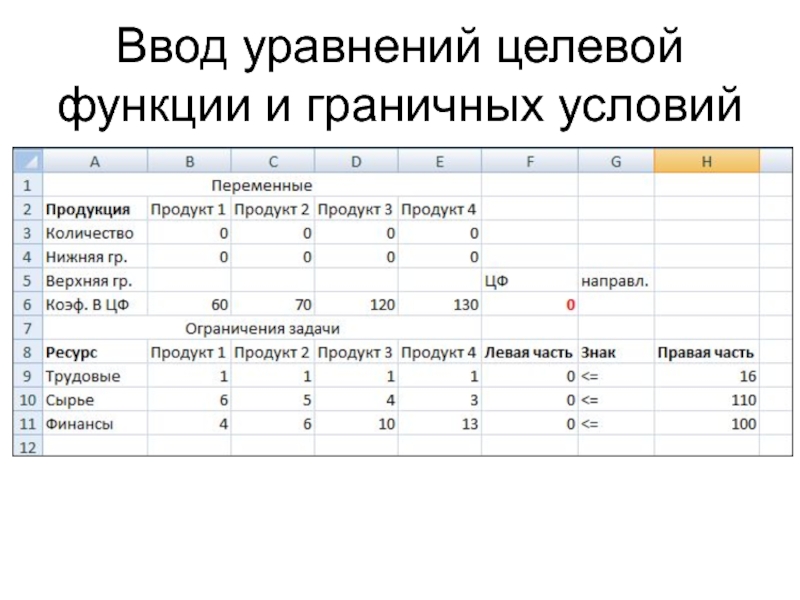
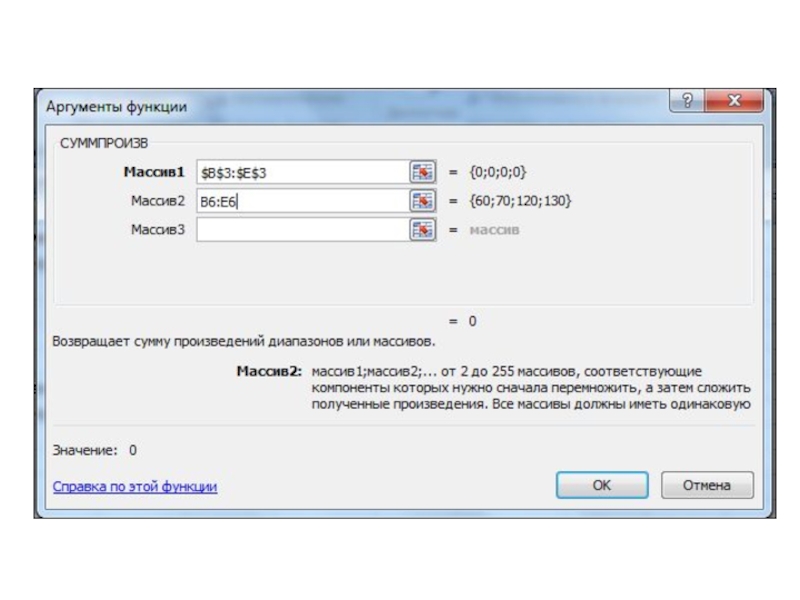
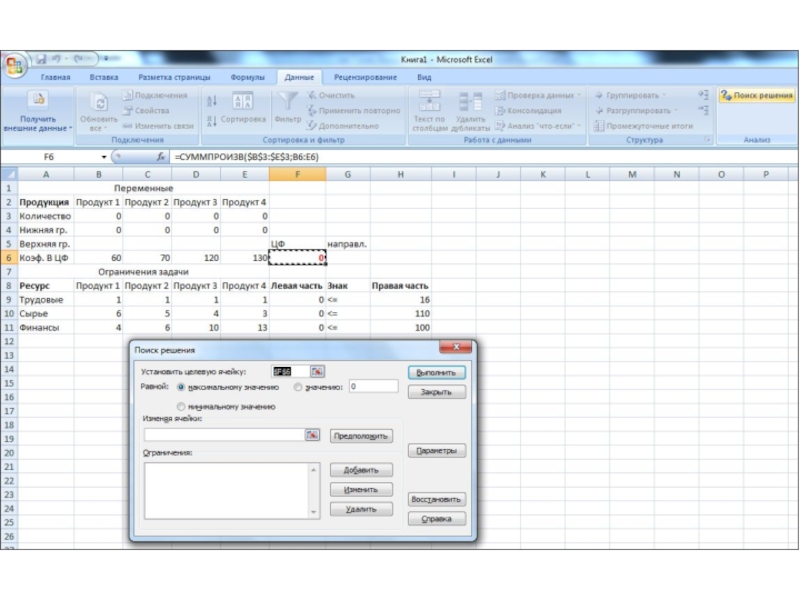
Слайд 25Ввод уравнений целевой функции и граничных условий
Слайд 28Дальнейшее решение задачи проводится с использованием надстройки Поиск решения табличного
процессора MS Excel.
Поиск решения является надстройкой MS Excel, инструментом для
поиска решения уравнений и задач оптимизации.
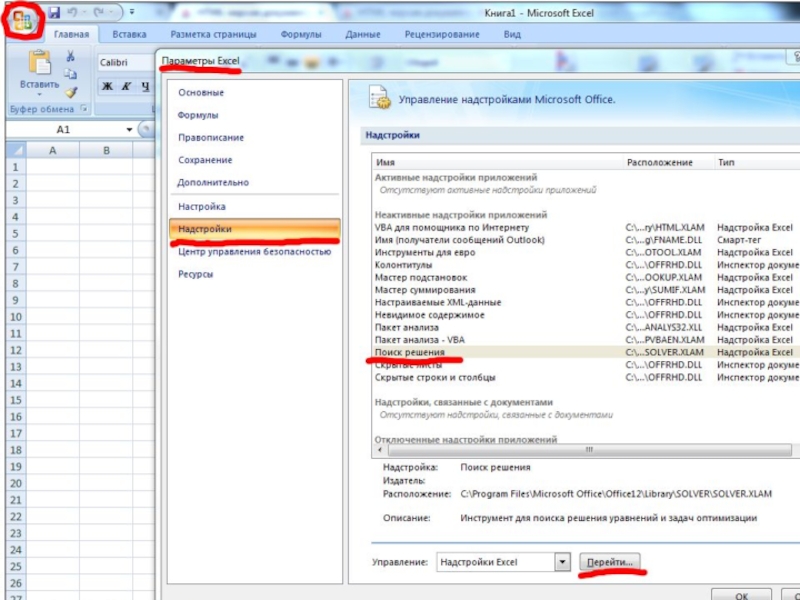
Данная надстройка, в случае отсутствия в пунктах меню MS Excel 2003 и более ранних версий, может быть добавлена с помощью выбора пунктов Сервис – Надстройки – Поиск решения.
После этого будет добавлен подпункт Поиск решения в меню Сервис.
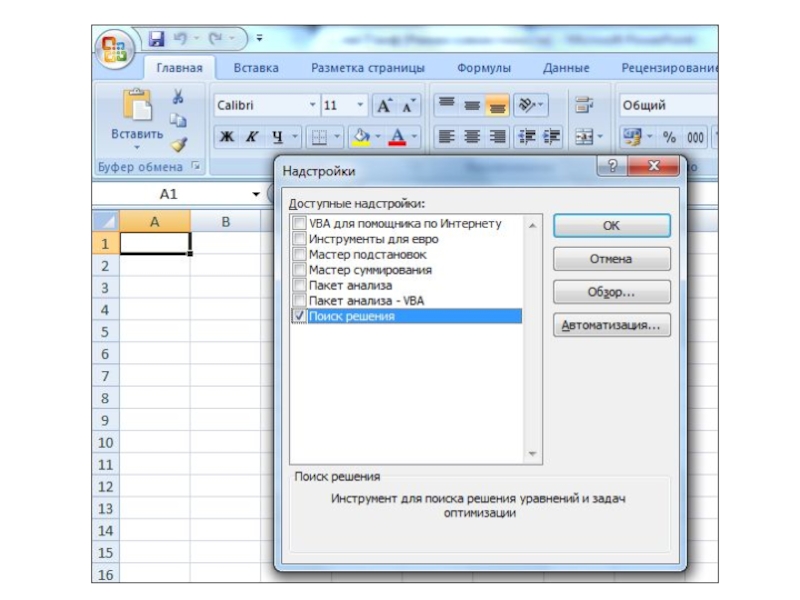
В MS Excel 2007 надстройка добавляется следующим образом.
Слайд 33Поясним смысл элементов окна Поиск решения.
Установить целевую ячейку - определяет
целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать
равным конкретному значению.
Изменяя ячейки - определяет изменяемые ячейки (искомые). Изменяемая ячейка - это ячейка, которая может быть изменена в процессе Поиска решения для достижения нужного результата в ячейке из окна Установить целевую ячейку с удовлетворением поставленных ограничений.
Предположить - отыскивает все неформульные ячейки, прямо или непрямо зависящие от формулы в окне Установить целевую ячейку, и помещает их ссылки в окно Изменяя ячейки.
Ограничения - перечисляет текущие ограничения в данной проблеме.
Добавить - выводит окно диалога “Добавить ограничение”, в котором можно добавить ограничения к текущей проблеме.
Изменить - выводит окно диалога “Изменить ограничение”, в котором можно модифицировать имеющиеся ограничения.
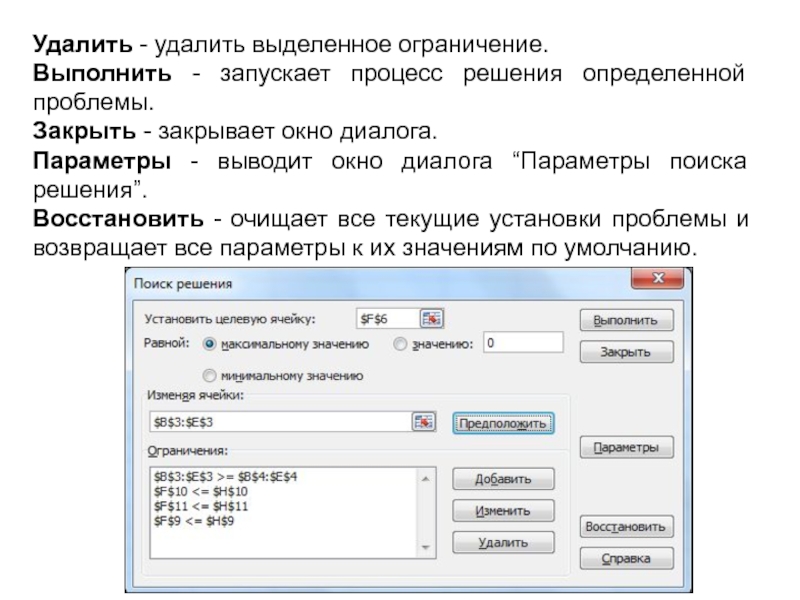
Слайд 34Удалить - удалить выделенное ограничение.
Выполнить - запускает процесс решения определенной
проблемы.
Закрыть - закрывает окно диалога.
Параметры - выводит окно диалога “Параметры
поиска решения”.
Восстановить - очищает все текущие установки проблемы и возвращает все параметры к их значениям по умолчанию.